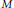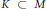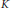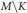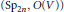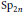Contents
Research Article
Hölder Compactification for Some Manifolds with Pinched Negative Curvature Near Infinity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1201-1218
-
- Article
-
- You have access
- Export citation
CR Extension from Manifolds of Higher Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1219-1239
-
- Article
-
- You have access
- Export citation
Categorification of the Colored Jones Polynomial and Rasmussen Invariant of Links
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1240-1266
-
- Article
-
- You have access
- Export citation
Nonadjacent Radix-τ Expansions of Integers in Euclidean Imaginary Quadratic Number Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1267-1282
-
- Article
-
- You have access
- Export citation
Remarks on Littlewood–Paley Analysis
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1283-1305
-
- Article
-
- You have access
- Export citation
Theta Lifts of Tempered Representations for Dual Pairs (Sp2n ,O(V))
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1306-1335
-
- Article
-
- You have access
- Export citation
Moving Frames for Lie Pseudo–Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1336-1386
-
- Article
-
- You have access
- Export citation
On n-Dimensional Steinberg Symbols
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1387-1405
-
- Article
-
- You have access
- Export citation
Hauteur asymptotique des points de Heegner
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1406-1436
-
- Article
-
- You have access
- Export citation
Other
Index of Volume 60
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1437-1440
-
- Article
-
- You have access
- Export citation