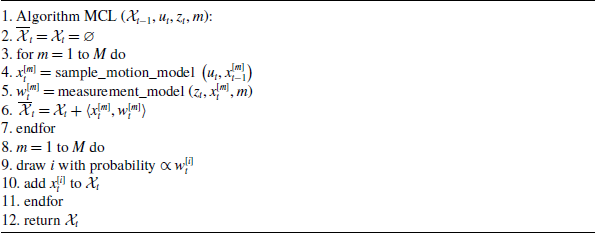Global localization for mobile robots in symmetrical indoor environments: a review, practical challenges, and experimental validation

Abstract

Efficient global localization of mobile robots in symmetrical indoor environments remains a formidable challenge, given the inherent complexities arising from uniform structures and a dearth of distinctive features. This review paper conducts an in-depth investigation into the nuances of global localization strategies, focusing on symmetrical environments, such as extended corridors, symmetrical rooms, tunnels, and industrial warehouses. The study comprehensively reviews and categorizes key techniques employed in this context, encompassing probabilistic-based approaches, learning-based approaches, Simultaneous Localization and Mapping (SLAM)-based approaches, and optimization-based approaches. The primary goal is to provide a contemporary and thorough literature review, offering insights into existing global localization solutions, followed by extant methods tailored for symmetrical indoor spaces. Also, the paper addresses practical challenges associated with implementing various global localization techniques, contributing to a holistic understanding of their real-world applicability. Comparative experimental results demonstrate that hybrid approaches achieve superior localization accuracy in symmetrical environments compared to any single method alone. These experiments, conducted in indoor settings with different symmetry levels, highlight the hybrid approach’s robustness and precision in resolving symmetry-induced ambiguities. This work signifies a significant step forward in mobile robot global localization, which addresses symmetrical environments’ complexities by leveraging the strengths of hybrid methodologies.

1. Introduction

Over the past few decades, wheeled autonomous mobile robots have become widely utilized in factories, shopping malls, and homes to perform various service tasks due to their ability to navigate independently in indoor environments. A key component of this autonomous navigation capability is accurate localization, which enables the robot to determine its position and provides essential input for planning and control processes. Localization is particularly critical among the various capabilities required for effective robot operation. Inaccurate or unreliable localization can lead to navigation failures or even collisions, underscoring its importance in ensuring safe and efficient robot performance.

Global localization is a fundamental problem in mobile robotics that involves determining a robot’s position and orientation within a known environment without prior knowledge of its initial location. This challenge is critical for autonomous navigation, especially in indoor environments where global positioning system (GPS) signals are often unavailable [1]. Successful global localization enables a robot to navigate, map, and interact with its surroundings autonomously. It is essential for various applications, from service robots in homes and offices to automated guided vehicles in warehouses. Figure 1 shows how global localization is intricately connected to mobile robots’ navigation, guidance, and control, forming a fundamental aspect of their autonomous operation. Global localization gives the robot an accurate understanding of its position within a global coordinate system, essential for effective navigation and precise waypoint following. It ensures accurate guidance by continuously updating the robot’s position, maintaining the desired trajectory, and avoiding deviations. Additionally, it supplies crucial feedback for control systems, enabling precise adjustments to the robot’s movements based on its current state.

Figure 1. Overview of an autonomous mobile robot system.

The paper broadly classifies the overview of existing methods for global localization into probabilistic-based, learning-based, Simultaneous Localization and Mapping (SLAM)-based, and optimization-based approaches.

(i) Probabilistic-based approaches: Bayesian filters, like the extended Kalman filter (EKF) and the particle filter, fall under this category. They use probabilistic models to estimate the robot’s global pose by incorporating sensor measurements and motion models. (ii) Learning-based approaches: Learning-based approaches aim to capture complex relationships between sensor inputs and global poses, reducing reliance on explicit models. (iii) SLAM-based approaches: SLAM methods involve building a map of the environment while simultaneously localizing the robot within the map. SLAM methods can be broadly classified based on the primary sensors they use into three categories: Light Detection and Ranging (LiDAR)-based SLAM, Vision-based SLAM (VSLAM), and Hybrid SLAM. Each of these methods leverages different types of sensor data to build maps and localize the robot within an environment. (iv) Optimization-based approaches: Optimization-based approaches for mobile robot localization focus on formulating the localization problem as an optimization problem. The objective is to find the robot’s pose (position and orientation) that minimizes (or maximizes) a certain cost (or reward) function.

Indoor environments often pose unique challenges for global localization, particularly when they are symmetrical or lack distinctive features. These symmetrical environments, as shown in Figure 2, can adversely affect the global localization of mobile robots due to the challenge of observing a large quantity of similar structures with few distinct features in these settings [2, 3]. These scenarios intensify the problem of global localization, requiring more sophisticated algorithms to determine the robot’s position reliably. Current solutions depend on approaches such as artificial landmarks [2], QR codes [4], etc. Furthermore, achieving global localization usually requires more than just a few sensor scans to succeed [5, 6], especially in the case of symmetric environments.

Figure 2. Symmetrical scenarios: (a) office environment, (b) tunnel, (c) industrial warehouse, and (d) long corridors.

Despite significant advancements, several gaps and challenges remain in the field of global localization:

• • Ambiguity in symmetrical environments: Numerous existing methods [5–10] struggles with accurately localizing the robot in environments with repetitive patterns or symmetrical structures. In these environments, the robot may encounter difficulties distinguishing one location from another due to the repetitive nature of the surroundings. For instance, if a corridor looks identical from one end to the other, the robot’s sensors may provide similar readings in multiple locations, leading to ambiguity about its exact position.

• • Featureless regions: Regions with few or no distinctive features can lead to poor localization performance due to the lack of reference points.

Examples include empty hallways, large open spaces, or plain walls. In these regions, sensors like cameras or LiDAR may struggle to find enough data points or features to determine the robot’s position accurately. Without adequate reference points, the robot may have trouble accurately understanding its location, leading to potential errors in navigation.

• • Sensor noise and inaccuracies: Sensor data is often noisy and may lead to incorrect localization, especially in dynamic or cluttered environments.

For instance, a LiDAR sensor might pick up reflections from shiny surfaces or moving objects, leading to false readings. Similarly, cameras can be affected by varying lighting conditions, and inertial measurement units (IMUs) can drift over time.

• • Computational complexity: The high computational demands of some localization methods limit their real-time applicability on resource-constrained robots.

Global localization algorithms often require complex computations to process sensor data, map the environment, and estimate the robot’s position. The algorithms, such as particle filters, graph-based optimization, or deep learning models, are computationally intensive. Over high computational load can cause delays, reducing the robot’s ability to respond effectively to its environment.

• • Adaptability: Many algorithms are environment-specific and struggle to generalize across different indoor settings.

Researchers design existing localization algorithms with specific environments in mind. They rely on particular features, sensor configurations, or assumptions about the environment that do not generalize well to different settings. For example, an algorithm optimized for a well-lit office environment might perform poorly in a dimly lit warehouse.

Therefore, this review paper aims to address these gaps and challenges by

1. 1. Analyzing state-of-the-art methods in global localization: Providing a comprehensive overview of current global localization techniques like adaptive Monte Carlo localization (AMCL), Hector SLAM, cartographer, and hybrid SLAM, highlighting their strengths and weaknesses in symmetrical environments. The importance of this analysis lies in understanding how these techniques perform under specific conditions of symmetry and what limitations they may have. By critically evaluating these methods, the review highlights which approaches are most effective and where improvements are needed.

2. 2. Addressing critical challenges in global localization imposed by symmetrical environment: Discussing the challenges posed by symmetrical indoor environments, such as symmetrical features and a lack of distinct landmarks, which can complicate localization tasks. Understanding these critical challenges is crucial for improving the robustness and reliability of localization systems. Pinpointing where the current methods fall short and exploring possible solutions aims to provide insights into how to address these challenges effectively.

3. 3. Benchmarking performance: Establishing a benchmark scenario by constructing a symmetrical environment to evaluate localization algorithms and presenting a comparative analysis based on these benchmark scenarios. Comparative analysis based on this benchmark scenario clearly shows how different methods perform in controlled conditions. The rationale behind benchmarking is to provide a standardized framework for assessing algorithm performance, which helps identify best practices and improvement areas.

This paper offers several significant contributions to global localization in symmetrical environments. First, it presents a comprehensive review and critical analysis of prominent localization techniques including AMCL, Hector SLAM, Cartographer, and hybrid SLAM highlighting their advantages and limitations when applied in highly symmetrical settings. Second, it systematically identifies the core challenges posed by symmetrical environments, such as the scarcity of distinctive landmarks and the presence of repetitive structural features, and provides informed insights into potential strategies for improving localization robustness under such conditions. Third, the paper introduces a benchmarking framework that involves the design of a controlled, standardized symmetrical environment, enabling consistent evaluation and comparison of localization algorithms. This framework facilitates the identification of best-performing methods and highlights areas requiring further improvement. Collectively, these contributions aim to deepen the understanding of localization in geometrically ambiguous spaces and support the development of more resilient and accurate systems.

While review papers [11–13] explore localization in robotics, they primarily emphasize theoretical frameworks and general algorithmic categories. They often overlook the practical and critical challenges posed by global localization in symmetrical environments, where repetitive spatial structures introduce pose ambiguity, aliasing, and belief collapse issues that can drastically degrade localization accuracy. Furthermore, existing surveys rarely systematically examine how different algorithms cope with environmental symmetry in real-world scenarios. They also lack benchmark-driven evaluations that explore the computational burden and robustness of these methods under controlled, variable-symmetry conditions. This paper addresses these limitations by narrowing its focus to the global localization problem under symmetry-induced uncertainty. It reviews state-of-the-art techniques including probabilistic-based, learning-based, SLAM-based, and optimization-based approaches. To ground the discussion, the paper introduces two experimental test cases (low and high symmetry) that help reveal practical performance boundaries. These gaps and limitations form the core motivation of this review to provide a practically guided and symmetry-aware perspective that advances the understanding and application of global localization techniques in complex indoor environments.

This review paper begins by categorizing the fundamental challenges of global localization for indoor mobile robots into probabilistic, learning-based, SLAM-based, and optimization-based approaches based on their underlying methodologies and techniques to estimate a robot’s position within an environment. Figure 3 shows a general classification of such methods:

Figure 3. Classification of indoor global localization approaches.

Section 2 presents a detailed examination of the four primary categories for global localization. The discussion thoroughly explores each category, highlighting the specific methodologies and their respective applications in estimating a robot’s position within an environment. This comprehensive analysis aims to elucidate each approach’s distinct characteristics and advantages, offering a nuanced understanding of their roles in advancing localization accuracy and efficiency.

Section 3 delves into the critical issue of global localization when encountering a symmetrical indoor space, a significant challenge in robotics due to these environments’ inherent ambiguities. It also evaluates existing solutions, including integrating visual features with traditional LiDAR-based methods and combining vision sensors with probabilistic localization techniques, to enhance localization accuracy in these environments.

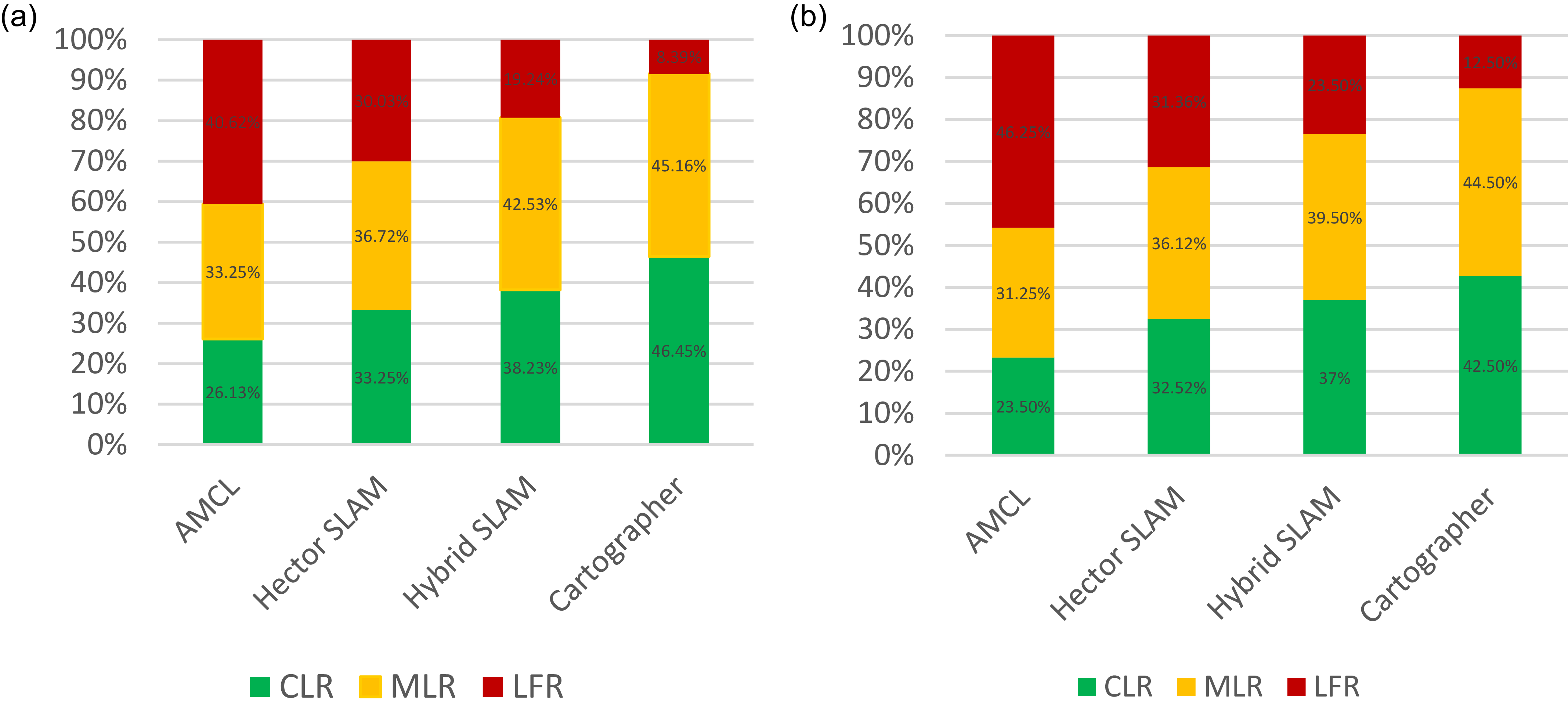
In Section 4, this paper presents a comparative analysis of four algorithms (AMCL, Hector SLAM, hybrid SLAM, and Cartographer) operating in low- and high-symmetry scenarios. It provides corresponding experimental findings and insights. Section 5 presents a comprehensive discussion of our findings, interpreting the results within the context of existing literature and analyzing their implications for the field. Section 6 gives conclusions, emphasizing current challenges and outlining potential directions for future research endeavors.

2. Review of global indoor localization of mobile robots

2.1. Localization principle

The mobile robot utilizes odometry to track its movement while traversing in a familiar environment. However, the inherent uncertainty in odometry measurements can lead to confusion regarding the robot’s precise position. The robot employs localization techniques to mitigate this uncertainty and accurately understand its location relative to the environment. The robot collects observations about its surroundings by incorporating information from its external sensors, including laser, vision, and ultrasonic sensors. These sensory inputs offer valuable data for a more robust understanding of the environment and the robot’s position. The robot enhances its localization capabilities by integrating these sensory observations with the data obtained from odometry. This fusion of information allows the robot to refine its estimate of its current position, effectively reducing the potential for position uncertainty to escalate uncontrollably.

In summary, by leveraging odometry data and information gathered from its exteroceptive sensors, the mobile robot can localize itself within its environment, thereby mitigating the effects of odometry uncertainty and maintaining a reliable understanding of its position.

2.2. Localization approaches

Global localization for mobile robots is classified into four approaches based on underlying methods and techniques used to determine the robot’s location: probabilistic-based, learning-based, SLAM-based, and optimization-based approaches.

2.2.1. Probabilistic-based approaches

Probabilistic approaches in robotics employ probability theory to manage uncertainties inherent in sensor data and robot motion. Two prominent methods within this framework are Kalman filters and particle filters.

Kalman filters: These are optimal estimators for linear systems with Gaussian noise. They maintain a belief about the robot’s state as a Gaussian distribution, updating this belief through a prediction–correction cycle.

Particle filters (Monte Carlo Localization – MCL): These are nonparametric approaches suitable for nonlinear and non-Gaussian systems. They represent the robot’s belief as a set of weighted samples (particles), each hypothesizing a possible state.

Kalman filter

Kalman filter [11] is widely used for localizing mobile robots because it estimates the state of a dynamic system from a series of noisy measurements. It is one of the most commonly used methods for sensor fusion in mobile robotics applications [12]. This filter frequently combines data from sensors to create a statistically optimal estimate. If a system describes a linear model and models the uncertainties of the sensors and the system as white Gaussian noise, the Kalman filter provides an optimal statistical estimate for the observed data.

Figure 4 represents the schematic diagram of applying the Kalman filter to localize the mobile robot. The algorithm works by a two-phase process with prediction and update phases. (i) In the prediction step, the Kalman filter predicts the current state of the robot based on the mathematical model of its motion (e.g., how it should move given the control input like velocity or steering angle) and the previous state estimate. The filter also predicts the uncertainty associated with its state estimate, which grows over time due to uncertainties in the model and the control inputs. (ii) In the update step, the Kalman filter updates its state estimate once it gets new sensor data. It compares the predicted state to the actual sensor measurements and uses this “innovation” to correct the state estimate. The filter then reduces the uncertainty in the state estimate based on how reliable the sensor data is. Thus, Kalman filter-based localization efficiently and accurately addresses the challenge of tracking a robot’s position. This optimal sensor fusion method is particularly effective when monitoring the robot’s movement from an initially known location. Typically employed in continuous world representation, this localization method encounters limitations when the robot’s uncertainty becomes substantial, such as when the robot’s initial pose is unknown. In such cases, the localization approach fails to capture potential robot positions accurately and irreversibly loses track.

Figure 4. Schematic diagram of Kalman filter-based mobile robot localization.

In the realm of Kalman filter theory, the assumption is that the system is linear and characterized by Gaussian noise. Nevertheless, numerous robotic systems exhibit nonlinear characteristics. This necessity has led to the development of an alternative localization method called the EKF. The EKF is an extension of the Kalman filter tailored for nonlinear systems. In the EKF, the initial step involves linearizing the system and applying the Kalman filter. In [13], the localization of a mobile robot using EKF was presented, which used a nonlinear model to predict the coordinates of a wheeled mobile robot. To improve the localization performance and to reduce accumulated errors while using dead reckoning, a method that uses EKF with an infrared sensor was proposed [14]. Studies reported in ref. [15] and [16] employed various sensors like sonar, IMU, and encoders along with EKF for the localization of a mobile robot. Despite the performance improvements in these methods, EKF faced limitations when applied to mobile robot localization, particularly due to its reliance on linearizing nonlinear systems [17], which led to significant errors. EKF’s performance was affected by inaccurate covariance propagation and the complexity of computing Jacobians, which were often error-prone [18]. Additionally, it assumes Gaussian noise, which may not hold in real-world scenarios.

In ref. [19], the authors addressed the above issues with EKF and introduced the Unscented Kalman Filter (UKF), which used the unscented transform to propagate sigma points through the nonlinear system without linearization. UKF resulted in higher accuracy, better handling of nonlinearities, and robustness to non-Gaussian noise, making UKF more suitable for complex mobile robot localization tasks. UKF overcomes EKF linearization errors using a deterministic sampling approach, representing the state distribution as a set of sample points, and achieves better accuracy [20]. The study based on real data shows that the performances of the EKF and UKF are nearly identical to those in ref. [21]. In the Kalman filter approach, the system requires knowledge of the robot’s initial position with some approximations. As a result, it does not solve the global localization problem. Also, Kalman filters represent uncertainty as a single Gaussian distribution, which is limited when the robot’s belief about its position could have multiple possible solutions (e.g., in environments with symmetry or ambiguity).

Figure 5. Monte Carlo localization for mobile robot localization [22].

Particle filter

EKF estimation assumes that noise from sensors and the environment follows a Gaussian probability density function. In practice, this assumption may not always hold. Additionally, some sensors have strongly nonlinear measurement models, which leads to increased estimation errors when linearizing the nonlinear equations. When these assumptions are not suitable, the particle filter is a more appropriate algorithm for global localization of mobile robots. It processes raw sensor data directly, eliminating the need to extract features from sensor values. Unlike the EKF, which is bound to a unimodal distribution, particle filters are nonparametric and do not rely on a Gaussian density assumption. The particle filter algorithm also uses increasingly sophisticated methods to represent uncertainty, surpassing the limitations of the standard Kalman filter. We now turn our attention to a popular localization algorithm that describes the belief bel(x _t ) by particles. The algorithm is called MCL. The MCL has emerged as one of the most widely adopted localization algorithms in robotics due to its popularity and effectiveness. Its straightforward implementation and versatility make it suitable for addressing various robot localization challenges with generally favorable outcomes.

Figure 5(a–e) illustrates MCL using the one-dimensional hallway example [22]. Initially, the robot does not know exactly where it is. Therefore, it randomly guesses by placing several possible positions (represented as particles) all over the map. As the robot senses its surroundings, it can refine its position estimate by continuously updating and resampling particles based on sensor data and movement. As the robot gathers more information, it increasingly focuses on the most likely locations, improving its accuracy of localization. This process ensures that the robot’s position estimate converges towards the proper location over time.

Table I shows the MCL algorithm based on particle filter, obtained by substituting the appropriate probabilistic motion and perceptual models into the particle filter algorithm shown in Table II. The basic MCL algorithm represents the belief $\mathrm{bel} (x_{t})$ by a set of $M$ particles:

(1) \begin{equation}\mathcal{X}_{t}=\left\{x_{t}^{\left[1\right]},x_{t}^{\left[2\right]},\ldots ,x_{t}^{\left[M\right]}\right\}\end{equation}

Line 4 in the algorithm (Table I) samples from the motion model, using particles from the present belief as starting points. The measurement model is then applied in line 5 to determine the important weight of that particle. The initial belief $\mathrm{bel} (x_{0})$ is obtained by randomly generating $M$ such particles from the prior distribution $p(x_{0})$ and assigning the uniform importance factor $M^{-1}$ to each particle. The function’s motion model predicts the next state of particles based on robot dynamics, while the measurement model updates the particle weights by predicted sensor observation with actual sensor data.

Table I. Monte Carlo localization (MCL) algorithm based on particle filters.

Table II. The particle filter algorithm.

In early works, the MCL algorithm relies on particle filter and uses a large number of weighted particles from the proposed distribution of robot pose and then updates them based on the measurement of sensors. The MCL algorithm always converges to the global optimum, but in large-scale scenes, it may take a lot of particles and a long time to converge [23]. To make sampling more efficient, many researchers have improved the MCL algorithm. For instance, the mixture algorithm combines the MCL algorithm with the dual MCL, using the probabilistic mixing ratio. Sometimes, it reduces the error by more than an order of magnitude compared to the original MCL. Self-adaptive Monte Carlo localization (SAMCL) distributes global samples in a similar energy region instead of distributing them randomly on the map, which results in better localization performance [24]. However, they depend on the specific environment, which makes them unreliable, and they are still unable to solve the slow convergence problem in large-scale environments. The MCL method is still the gold standard for robot localization and often uses LiDARs [25–27], cameras [28], or Wi-Fi [29]. Such MCL methods often use a 2D LiDAR sensor and an occupancy grid map to estimate the robot’s pose, and they are quite robust.

2.2.2. Learning-based approaches

This paper section focuses on learning-based methods for achieving global localization for indoor mobile robots. These methods leverage machine learning algorithms to interpret sensor data and predict the robot’s location. The system can recognize patterns and improve localization accuracy over time by training on large datasets. Learning-based approaches for global localization can be classified into three main categories: supervised learning, unsupervised learning, and reinforcement learning (RL) based on the learning process involved.

Supervised learning approaches involve training a model on a labeled dataset, where the input data (e.g., LiDAR scans) are paired with the corresponding output labels (e.g., specific locations or poses). The model learns to map inputs to outputs based on the provided labels.

Unsupervised learning approaches do not rely on labeled data. Instead, they aim to find patterns or structures in the input data without explicit output labels.

RL involves training an agent to make a sequence of decisions by rewarding it for good actions and penalizing it for bad ones. In the context of localization, RL can be used to optimize the robot’s navigation and localization strategies based on its interactions with the environment.

Researchers have recently achieved global localization of mobile robots by incorporating environmental information about the robot’s location, which can be accomplished through semantic place classification. It involves assigning semantic labels or categories to different locations or areas within an environment based on their characteristics or attributes. This classification provides contextual information about the environment, which can be valuable for place recognition. By associating semantic labels with specific places, the robot can better understand the environment and distinguish between locations based on their semantic meaning rather than just raw sensor data. This approach enhances the reliability and accuracy of place recognition, particularly in complex indoor environments where traditional methods may struggle due to similarities in sensor data. Presented in ref. [30], the semantic model of the indoor environment provides the robot with a representation closer to human perception, thereby enhancing the navigation task. Also, incorporating semantic information into the map improves the accuracy of robot navigation, as in ref. [31]. The semantic model of the indoor environment provides the robot with a representation closer to human perception, thereby enhancing the navigation task.

“Semantic place labelling” or “semantic place classification” can be performed by making use of data acquired from its sensors [32]. Classification methods based on visual data captured with a 2D camera [33] or fused data [34], including the visual and range data acquired from a 2D laser range finder, have been studied previously. In these studies, researchers generally extracted features such as Scale-Invariant Feature Transform (SIFT) [35] and Speeded Up Robust Features (SURF) [36] from images or calculated hand-crafted features from laser range data. They then processed these features to classify a robot location. The main drawback of the studies using visual data is the performance dependency on illumination variations corresponding to different lighting conditions.

The paper categorizes the related work on semantic place classification into supervised and unsupervised learning methods based on how the semantic information is learned. This semantic information might sometimes be uncertain, especially in environments with symmetrical or repetitive structures. In such cases, RL-based algorithms can incorporate uncertainty into their decision-making processes, allowing robots to weigh different possibilities and choose actions that reduce ambiguity. Also, RL can learn robust policies for localization in the presence of sensor error, noise, or unexpected environmental changes. Based on this, learning-based approaches are classified into supervised, unsupervised, and RL.

Supervised learning

In recent years, the application of supervised machine learning techniques has significantly advanced the field of robotic place recognition and semantic mapping to improve global localization. Researchers have developed various models and algorithms to enhance a robot’s ability to understand the environment and navigate complex environments.

For instance, a bubble space model presented in ref. [37] for place representation contained two new variables: varying robot pose and multiple features. These variables were transformed into bubble descriptors and classified by a multi-class support vector machine (SVM) classifier to learn specific places. A Voronoi Random Field (VRF) algorithm [38] was proposed, based on Conditional Random Field, and an SVM classifier was used to achieve semantic labeling of Generalized Voronoi Graphs nodes. A low-level image descriptor for addressing the room classification problem was proposed by refs. [39] and [40] using an SVM classifier. A semantic map construction method, which combined place and object recognition using supervised learning, was presented in ref. [41]. High-dimensional histograms were used to represent an observed scene and achieved the classification of visual places through SVM [42]. Performance was evaluated using the Freiburg University, Buildings 79 and 52 dataset [43].

Unsupervised learning

In global localization, supervised learning approaches rely on labeled datasets, requiring human intervention to annotate data for training. In contrast, unsupervised learning methods offer several advantages. They eliminate the dependency on labeled data, allowing models to discover new patterns and relationships in raw, unlabeled data. Unsupervised models can autonomously extract features and find patterns in the data, enabling the robot to learn, classify the places, and adapt to new environments without explicit human intervention. Additionally, these methods can incrementally learn and organize environmental data, allowing robots to update their understanding of surroundings in real time.

Recent advancements in semantic place classification using unsupervised learning have significantly improved global localization by leveraging various sensor modalities and machine learning techniques. Traditional approaches utilized visual cues from video and image streams to detect and categorize “unknown” place labels [44]. Additionally, a Gaussian mixture model was used to form a probability distribution of features extracted by image-preprocessing, while a place detector grouped features into places using odometry data and a hidden Markov model [45]. The unsupervised method proposed in ref. [46], based on the Single-Linkage (SLINK) agglomerative algorithm [47] and an incremental approach, allows the robot to learn about organizing the observed environment and localizing within it. Finally, the authors in ref. [48] used CENsus TRansform hISTogram (CENTRIST) and GIST descriptors, applying an unsupervised approach with a Self-Organizing Map for classification.

Incorporating semantic place recognition to enhance global localization using unsupervised learning was applied to various sensors, including 2D and 3D LiDARs, red, green, blue (RGB), and red, green, blue-depth (RGB-D) cameras. In ref. [49], AdaBoost features from 2D LiDAR scans were used to infer semantic labels such as office, corridor, and kitchen. They combined the semantic information with an occupancy grid map in an MCL framework. This method required a detailed map and a manually assigned semantic label to every grid cell. According to ref. [50], researchers constructed semantic maps from cameras by assigning a place category to each occupancy grid cell. They used the Places205 ConvNet to recognize places and relied on a LiDAR-based SLAM for building the occupancy grid map. In ref. [51], available building information models (BIMs) were used to extract and localize geometric and semantic information by matching 2D LiDAR-based features corresponding to walls, corners, and columns. While the automatic extraction of semantic and geometric maps from a BIM was promising, it was not suitable for global localization due to its inability to overcome the challenges of a repetitively structured environment.

Recent works in extracting semantic information with deep learning models showed significant improvement in the performance of mobile robot localization using text spotting. Using textual cues for localization was surprisingly uncommon, with notable works presented in refs. [52] and [53]. The study in ref. [52] presented a novel underground parking localization method using text recognition, employing optical character recognition (OCR) to detect parking slot numbers and combining OCR with a particle filter for localization. In ref. [53], an indoor localization system for dynamic environments was presented, using text spotting integrated into an MCL framework, which operated on 2D LiDAR scans and camera data.

Reinforcement learning

Building upon exploring supervised and unsupervised learning approaches in global localization, RL emerges as a pivotal technique in enabling mobile robots to navigate and understand complex environments autonomously. Unlike traditional methods, RL allows an agent to learn optimal behaviors through trial-and-error interactions within its environment, receiving feedback as rewards or penalties [54]. The key idea of RL is to determine the mapping between actions and states to maximize a numerical reward signal. The learner agent interacts with the environment and receives rewards or penalties for the performed actions. Therefore, RL uses rewards and punishments as signals for positive and negative behaviors to optimize agent behavior continuously.

Recent studies have demonstrated the efficacy of RL in addressing challenges associated with continuous state and action spaces noise in reward functions, as well as the integration of particle filters for improved state estimation. In ref. [47], a novel framework that utilizes a particle filter for learning in real-world situations was presented. This approach dealt with the challenge of expressing continuous states and actions by dividing the continuous state and action space, allowing a more efficient search for solutions with fewer memories and parameters. The study in ref. [55] addressed deep RL agent performance degradation due to noise in reward functions and proposed a novel filter to mitigate its effect. The proposed algorithm combined optimal filtering and RL concepts to improve the RL policy in the presence of skewed probabilistic distributions in reward functions. The method in [56] combined the ideas of particle filters, which are used for state estimation in nonlinear and non-Gaussian systems, with RL. This approach assigned randomness in the system and measurement models to the RL policy, allowing for optimization of various objective functions, such as estimation accuracy, particle variance, likelihood of parameters, and regularization term. This interpretation enabled the particle filter design process to benefit from the RL’s learning capabilities, improving the particle filter’s overall performance and accuracy in estimating a system’s state. These advancements underscore the potential of RL to significantly enhance the performance and robustness of global localization systems for indoor mobile robots.

Recently, deep learning models showed notable advancements in global localization. PoseNet [57], based on GoogLeNet, was the first work to utilize deep learning for this purpose, demonstrating the effectiveness of convolutional neural networks (CNNs) for complex regression tasks. Bayesian PoseNet [58] extended this approach by leveraging uncertainty measures for estimating re-localization error and scene detection. LSTMNet [59] uses LSTM units to reduce the dimensionality of CNN outputs, while Vidloc [60] employs video clips as input to improve pose estimation accuracy. HourglassNet [61] introduced an encoder–decoder CNN architecture with up-convolution layers to preserve fine-grained information. Branch Net [62] was a multi-task CNN addressing the coupling of orientation and translation. PoseNet2 [63] introduced a novel loss function for optimal learning of position and orientation, although its localization precision might decrease with scene scale.

A new approach recently emerged where deep learning was employed for robot localization. In refs. [64] and [65], deep CNNs were utilized for camera pose regression and initializing particles in MCL. In refs. [66], a collection of 2D laser data was converted into an RGB image and an occupancy grid map, which were combined into a multi-channel image. A neural network architecture was employed to predict the 3-DOF robot pose, with experiments conducted on an actual mobile robot to validate the efficacy of this approach. The methodology in ref. [67] uses a deep hierarchical framework for robot global localization, involving two main components: coarse localization and fine localization. Coarse localization used RGB images and a CNN-LSTM network, while fine localization combines fast branch-and-bound scan matching (FBBS) and MCL using LiDAR point cloud data. The framework achieved faster convergence and more accurate estimation compared to other methods. Deep learning-based object detection has gained the attention of researchers for robot semantic navigation. In ref. [68], a real-time semantic map production system for indoor robot navigation was proposed, utilizing LiDAR and vision-based systems, achieving 78.86% average map construction accuracy.

2.2.3. SLAM-based approaches

Over the past decades, significant progress has been made in advancing autonomous navigation for mobile robots. The development of SLAM technology is crucial in enhancing robots’ ability to localize themselves and construct detailed maps of their surroundings without prior knowledge of the environment. SLAM technology is the foundation for autonomous decision-making, planning, and control of robots, enabling them to explore unknown environments effectively.

This paper categorizes SLAM approaches based on the sensors employed during the localization process, focusing on three primary categories: LiDAR-SLAM, visual SLAM, and Hybrid SLAM.

LiDAR-SLAM: This approach utilizes LiDAR sensors to generate precise representations of the environment. It is particularly effective in scenarios where accurate distance measurements are crucial, such as autonomous driving and robotics operating in complex terrains.

Visual SLAM: Leveraging cameras, visual SLAM systems capture images to interpret and map surroundings. These systems are advantageous due to their cost-effectiveness and the rich contextual information they provide. However, its performance can be affected by lighting conditions and textured environments.

Hybrid SLAM: To harness the strengths of multiple sensors, Hybrid SLAM integrates data from various sources, such as LiDAR, cameras, and IMUs. This fusion enhances robustness and accuracy, compensating for the limitations inherent in individual sensor modalities. For instance, combining LiDAR’s precise distance measurements with the rich visual context from cameras can improve performance in diverse environmental conditions.

The subsequent sections provide an in-depth review of studies within each of these categories, analyzing their methodologies, applications, and contributions to the advancement of SLAM technologies.

LIDAR-based SLAM

LiDAR-SLAM uses LiDAR sensor data as the primary source of information, enabling it to achieve localization and mapping under diverse environmental conditions. Object information from LiDAR presents a series of scattered points with accurate angular and distance information, known as a point cloud. Generally, LiDAR-SLAM extracts and matches the features of two consecutive point cloud graphs taken at different times, calculates the relative motion, distance, and pose changes through LiDAR odometry, and completes the robot’s self-positioning.

The significant advantage of the LiDAR sensor is its relatively accurate range measurement, simple error model, stable operation in environments without direct glare from intense light, and relatively easy point cloud processing. LiDAR-SLAM is categorized into two types based on the LiDAR sensor: 2D LiDAR-SLAM and 3D LiDAR-SLAM. 2D LiDAR-SLAM is lower in cost and suitable for simple indoor environments. At the same time, 3D LiDAR-SLAM, though more expensive, is ideal for outdoor surveying and mapping and handles larger amounts of information.

A complete 2D LiDAR-SLAM involves a front-end incremental estimation part and a back-end mapping part. The front-end consists of two components: obtaining sensor data and scan matching. The back-end’s main task is to solve a nonlinear optimization problem. The first mainstream approach for the back-end is based on filtering, like the Bayesian estimation process. A representative algorithm was Gmapping [69], which only estimated the robot’s position at the current moment, resulting in low computational requirements. However, this method had the disadvantage that errors generated at a previous moment could not be corrected, potentially leading to suboptimal mapping, especially in large environments. The second method was primarily based on nonlinear optimization, with graph optimization widely used in LiDAR-SLAM. In graph-based SLAM, the robot’s pose was represented as a node or vertex, and the relationships between poses formed the edges. Errors accumulated during map building were optimized using the nonlinear least squares method to produce the final map. A typical algorithm employing this method was Cartographer [70]. Fast SLAM [71], introduced in 2002, was the first system capable of generating real-time, faster maps, but it suffered from high memory usage and significant particle dissipation issues. The Optimal RBPF [72] method was proposed to address these shortcomings, which optimized the Gmapping algorithm to mitigate particle degradation problems. Karto-SLAM [72], an early system, introduced the concept of sparsity in graph-based optimization, laying the groundwork for Cartographer. Cartographer improved accuracy and robustness by leveraging graph optimization techniques while reducing computational requirements, displacing several early filter-based methods.

Over the past several decades, 2D SLAM has been well developed. Still, certain challenging environments, such as fog, smoke, and dust, significantly impact 2D LiDAR SLAM as they cause the laser beams to scatter and reduce the accuracy of scans. With the introduction of Lidar Odometry and Mapping (LOAM), 3D SLAM addressed the influence of many environmental factors. 3D SLAM typically uses 3D LiDAR and odometer data as input data, and 3D point cloud maps, robot trajectory, or pose graph as output. Section 2.2.3(C) will summarize work related to the hybrid SLAM based on 3D LiDAR.

Vision-based SLAM

VSLAM [73] is a technique that enables a robot to build a map of its environment while simultaneously keeping track of its location within that environment, using visual information from one or more cameras. Unlike LiDAR-based SLAM, which relies on laser sensors, VSLAM primarily uses cameras to capture images of the surroundings. VSLAM can be divided into feature-based and direct-based methods, each differing in processing and utilizing visual data to estimate the camera’s pose and build a map of the environment.

Feature-based VSLAM methods: These methods detect and extract distinct features, such as corners, edges, or blobs, from images. Once extracted features are matched across consecutive frames to estimate the camera’s motion and incrementally build a map of the environment. Feature-based methods are known for their robustness in environments with rich textures and are less sensitive to changes in lighting conditions. However, they may struggle in scenarios with low-texture regions or repetitive patterns, where distinct features are scarce or ambiguous.

Direct-based VSLAM methods: In contrast, direct methods utilize the intensity values of all pixels in the image without prior feature extraction. They aim to minimize the photometric error between consecutive frames by directly aligning images based on pixel intensities. This approach allows for using all available image information, making it effective in environments with low texture where feature-based methods might fail.

Feature-based VSLAM methods

In the realm of VSLAM, algorithms that rely on feature detection and matching have been instrumental in enabling robots to navigate and map their environments effectively. Early stages of feature-based VSLAM, feature extraction primarily relied on corner detection methods such as Harris [74], Features from Accelerated Segment Test (FAST) [75], and Good Features to Track (GFTT) [76]. However, their reliability is often insufficient. Consequently, researchers now prefer more stable local image features. Modern VSLAM methods based on point features typically employ feature detection algorithms like SIFT [35], SURF [77], and Oriented FAST and Rotated BRIEF (ORB) [78] to extract key points for matching images and then determined the pose by minimizing reprojection error.

MonoSLAM [79], introduced in 2007, was recognized as the inaugural real-time monocular VSLAM algorithm. It was the first successful application of the SLAM methodology from mobile robotics to the ‘pure vision’ domain of a single uncontrolled camera, achieving real-time but drift-free performance. The key novel contributions included an active approach to mapping and measurement, using a general motion model for smooth camera movement, and solutions for monocular feature initialization and feature orientation estimation. In the same year, Parallel Tracking and Mapping (PTAM) [80] improved over MonoSLAM, addressing its instability over extended periods and in diverse environments. It was the first SLAM algorithm to employ nonlinear optimization in the back end, tackling the issue of rapid data growth in filter-based methods.

Additionally, PTAM introduced the separation of tracking and mapping into distinct threads. The front end utilized FAST corner detection to extract features and estimate camera motion, while the back end handled nonlinear optimization and mapping. This approach ensured real-time performance in camera pose calculation and maintained overall SLAM accuracy. However, due to the absence of a loopback detection module, PTAM could accumulate errors during prolonged operation.

In 2015, ORB SLAM [81] was proposed and considered a notable advancement over PTAM, as it integrated a loop closure detection module, effectively mitigating cumulative errors. In real time, this monocular visual SLAM system used ORB features to perform SLAM. The loop closure detection thread also used the word bag model named Directed Bag of Words (DBoW) [82] for loop closure. The loop closure method based on the BoW model could detect the loop closure quickly by detecting the image similarity and achieve good results in the processing speed and the accuracy of map construction. In subsequent years, ORB-SLAM2 [83] and ORB-SLAM3 [84] were introduced and became widely utilized visual SLAM solutions due to their real-time CPU performance and robustness. However, the ORB-SLAM series heavily depended on environmental features, which could pose challenges in environments lacking sufficient texture features to extract enough feature points.

The reliance of point feature-based SLAM systems on the quality and quantity of point features presents challenges, particularly in scenes with weak textures like corridors, windows, and white walls, affecting system robustness and accuracy, potentially resulting in tracking failures. Additionally, rapid camera movement, changes in illumination, and other factors can significantly degrade the matching quality and quantity of point features. Growing interest was in integrating line features into SLAM systems to enhance feature-based SLAM algorithms. Two endpoints, represented by lines and line features, were used in the SLAM system to detect and track the two endpoints of lines in small scenes. The system could use line features alone or combined with point-line features, which was groundbreaking in VSLAM research. In ref. [85], a line-based monocular SLAM algorithm is proposed, which uses lines as basic features, and the UKF as a tracking algorithm. Due to the absence of loop closure and the representation of line segments as infinite instead of finite, the practical application of the scheme becomes challenging. Both [86], which used a monocular camera, and [87], which used a stereo camera, adopted the line segment detection (LSD) algorithm to detect line features and then combined the point-line features in SLAM. This approach performed well, even when most point features disappeared. Furthermore, it improved the accuracy, robustness, and stability of the SLAM system, though its real-time performance was lacking.

Direct-based VSLAM methods

In the field of VSLAM, direct methods have emerged as a significant advancement by utilizing pixel intensity information directly, thereby preserving all image details and eliminating the need for feature extraction and matching. This approach enhances computational efficiency and demonstrates strong adaptability to environments with intricate textures.

The Dense Tracking and Mapping (DTAM) algorithm [88] was proposed as the first practical direct method of VSLAM. DTAM allowed tracking by comparing the input images with those generated by reconstructed maps, enabling precise and detailed reconstruction of the environment. However, it increased the computational cost of storing and processing the data, making it feasible to run in real time on a GPU. Large-Scale Direct (LSD)-SLAM [89] introduced a direct monocular SLAM algorithm that enabled large-scale, consistent maps construction with accurate pose estimation and real-time 3D environment reconstruction. The algorithm included a novel direct tracking method that detected scale-drift and a probabilistic solution to incorporate noisy depth values into tracking, enabling real-time operation on a CPU. In ref. [90], a semi-direct monocular visual odometry algorithm was introduced, offering precision, robustness, and faster performance compared to current state-of-the-art methods. Semi-Direct Visual Odometry (SVO) combines the advantages of the feature point and direct methods. The algorithm is divided into two main threads: motion estimation and mapping. Motion estimation was carried out by feature point matching, but mapping was performed through a direct method. The research work in ref. [91] proposed Direct Sparse Odometry (DSO), which effectively utilized image pixels, making it robust even in featureless regions and capable of achieving more accurate results than SVO. DSO calculated accurate camera orientation even when feature point detector performance was poor, improving the robustness in low-texture areas or with blurred images. DSO also employed geometric and photometric camera calibration for high-accuracy estimation. However, DSO only considered local geometric consistency, leading to inevitable cumulative errors, and it was not a complete SLAM system as it lacked loop closure and map reuse.

Both feature-based and direct-based VSLAM methods have their advantages and limitations. Feature-based methods are generally more robust against varying lighting conditions and can handle larger inter-frame motions due to their reliance on distinct features. However, they may require significant computational resources for feature extraction and matching. By leveraging raw pixel intensities, direct methods can perform well in low-texture environments and offer more accurate pose estimation in specific scenarios. Nevertheless, they can be sensitive to changes in lighting and may face challenges with large inter-frame motions.

Hybrid SLAM

The development of single-sensor SLAM systems is relatively mature, with LIDAR, cameras, and IMU being the standard sensors in SLAM systems. 3D LIDAR provides the system with rich structural information about the environment, but the data are often discrete and numerous. Cameras capture color and texture in the environment at high speed but cannot directly perceive depth, and they are often perturbed by light. IMU sensitively perceives weak changes in the system within a very short time, but long-term drift is inevitable. Each of these sensors has distinct characteristics with clear advantages and disadvantages.

Single-sensor SLAM systems are fragile and uncertain, and they cannot handle multiple complex environments, such as high-speed scenes, small spaces, and open and large scenes simultaneously. As a result, hybrid SLAM has become a new trend in SLAM system development. Hybrid SLAM systems use a combination of LIDAR, cameras, and IMUs, which can be categorized into loosely coupled or tightly coupled modes as shown in Figure 6.

Figure 6. Classification of hybrid SLAM based on LiDAR sensor.

Figure 7. An occupancy grid map which shows multiple hypotheses about the robot’s pose due to symmetry in the environment and similar lidar scans.

Loosely coupled systems: In loosely coupled systems, each sensor’s data is processed independently, and the results are later integrated to estimate the robot’s state. This approach simplifies the system architecture and reduces computational load. However, it may not fully exploit the complementary strengths of each sensor, potentially limiting accuracy in complex environments.

Tightly coupled systems: Conversely, tightly coupled systems integrate data from all sensors simultaneously, considering their interdependencies during processing. This method allows for more accurate state estimation, especially in challenging environments. However, it requires more computational resources and a more complex system design.

Recent advancements in hybrid SLAM have led to the development of systems combining LiDAR, cameras, and IMUs in loosely and tightly coupled configurations. In this paper, we categorize these works into LIDAR-IMU loosely coupled systems, Visual-LIDAR-IMU loosely coupled systems, LIDAR-IMU tightly coupled systems, and Visual-LIDAR-IMU tightly coupled systems, based on the coupling method of the system and the types of sensors being fused. The development of SLAM reflects a transition from loose coupling to tight coupling. First, we discuss Hybrid SLAM based on LIDAR, followed by visual SLAM.

Hybrid SLAM loosely coupled system

The emergence of loosely coupled systems has opened up a new stage in developing Hybrid SLAM systems. Until now, its application in low-cost platforms with limited computational power is still widespread.

• • LiDAR-IMU loosely coupled system

The majority of loosely coupled systems were found in earlier works. The research work on the LOAM [92] algorithm was the main reason why LIDAR-based 3D SLAM technology became popular and well-known. The LOAM method enabled real-time 3D mapping by combining high-frequency odometry with precise point cloud registration. LOAM aided in global localization by utilizing odometry algorithms to estimate the velocity of the lidar and correct distortion in the point cloud. By matching and registering point clouds, LOAM created a map that helped determine the position of the lidar in a global coordinate system. This process ensured accurate mapping and localization in real time, contributing to the overall success of the global localization task. Compared to the state-of-the-art LOAM, Lightweight and Ground-Optimized Lidar Odometry and Mapping (LeGO-LOAM) [93] is designed to be lightweight, allowing it to run efficiently on low-power embedded systems. The design minimizes the computational resources required for processing LiDAR data and performing pose estimation. It leveraged the presence of a ground plane in its segmentation and optimization steps. This ground-optimized strategy helped improve pose estimation accuracy by utilizing planar features extracted from the ground. LeGO-LOAM aided global localization by integrating loop closure detection and correction mechanisms within its SLAM framework.

• • LiDAR-vision-IMU loosely coupled system

LIDAR odometer degradation occurs in unstructured and repetitive environments. Even with the assistance of an IMU for positioning, it still cannot work correctly for long periods. In contrast, vision sensors that do not require specific structural features, such as edges and planes, but rely on sufficient texture and color information to accomplish localization. However, vision sensors cannot obtain in-depth information intuitively. Therefore, combining a camera with LIDAR provides a complementary solution. The authors of LOAM extended their algorithms by combining feature tracking of monocular cameras with IMU in V-LOAM [94]. Subsequently, the authors of V-LOAM released its iterative version, Lidar-Visual-Inertial Odometry and Mapping (LVIOM) [95]. The improved method presented a data processing pipeline to estimate ego-motion online and build a map of the traversed environment, leveraging data from a 3D laser scanner, a camera, and an IMU. Unlike traditional methods that used a sequential, multilayer processing pipeline, solving for motion from coarse to fine, the system used visual–inertial coupling methods to estimate motion and perform scan matching to refine motion estimation and mapping further. The resulting system enabled high-frequency, low-latency motion estimation and dense, accurate 3D map registration.

Hybrid SLAM tightly coupled system

• • LiDAR-IMU tightly coupled system

The study in [96] proposed a tightly coupled LIDAR inertial localization and mapping (LIOM) framework, which jointly optimized measurements from LIDAR and IMU. The accuracy of LIOM is better than that of LOAM. However, the proposed method has a limitation as it requires initialization. Also, slow-motion scenarios could lead to drift due to the relatively sparse local map during their runtime. The study in ref. [86] released a follow-up work, lidar inertial odometry (LIO) via smoothing and mapping (LIO-SAM) [97], which utilized a factor graph for multi-sensor fusion and global optimization, and employed local sliding window scan matching for real-time performance enhancement. However, since feature extraction relied on geometric environments, this method still could not work for a long time in open scenes, and LIO degradation persisted during extended movements in such environments. FAST-LIO [98] proposed an efficient and robust LIO framework based on tightly coupled iterative Kalman filters for UAV systems to address this. The method fused more than 1200 feature points in real time and achieved reliable navigation results in a fast-motion, noisy, cluttered environment. To prevent the growing time of building a k-d tree of the map, the system could only work in small environments (e.g., hundreds of meters). FAST-LIO2 [99], built on FAST-LIO, addresses the growing computation issue by introducing a new data structure, ikd-Tree, which supports incremental map updates at every step and efficient kNN inquiries. Benefiting from the drastically decreased computation load, the odometry was performed by directly registering raw LiDAR points to the map, improving the accuracy and robustness of odometry and mapping, especially when a new scan contained no prominent features.

• • LIDAR-Visual-IMU (LVI) tightly coupled system

The advanced framework of the LIO system has facilitated the development of the tightly integrated LVI system by leveraging the optimized LVI technology over the last couple of years. LiDAR and Visual Inertial Odometry Fusion (LVIO-Fusion) [100] was a robust SLAM framework that combined stereo camera, Lidar, IMU, and odometry data through graph-based optimization for accurate localization in urban traffic. The framework utilized a self-adaptive actor-critic method in RL to dynamically adjust sensor weights, enhancing system performance across various environments. Lidar-visual-inertial odometry via smoothing and mapping (LVI-SAM) [101] consisted of a Visual-Inertial System (VIS) and LIDAR-Inertial System (LIS). VIS can provide a pose prior for LIS, which provides pose estimation and accurate feature point depth for VIS initialization.

In addition, researchers developed a SLAM-based localization and navigation system for social robots, particularly the Pepper robot, to address the challenges of navigating dynamic indoor environments [102]. This system enhanced Pepper’s ability to autonomously navigate and interact with humans using advanced algorithms and sensor integration. Furthermore, researchers applied SLAM using an improved wall-follower approach to an autonomous maze-solving robotic system [103]. They also advanced the SLAM technique by fusing it with visible light positioning to improve robot localization and navigation, as demonstrated in ref. [104].

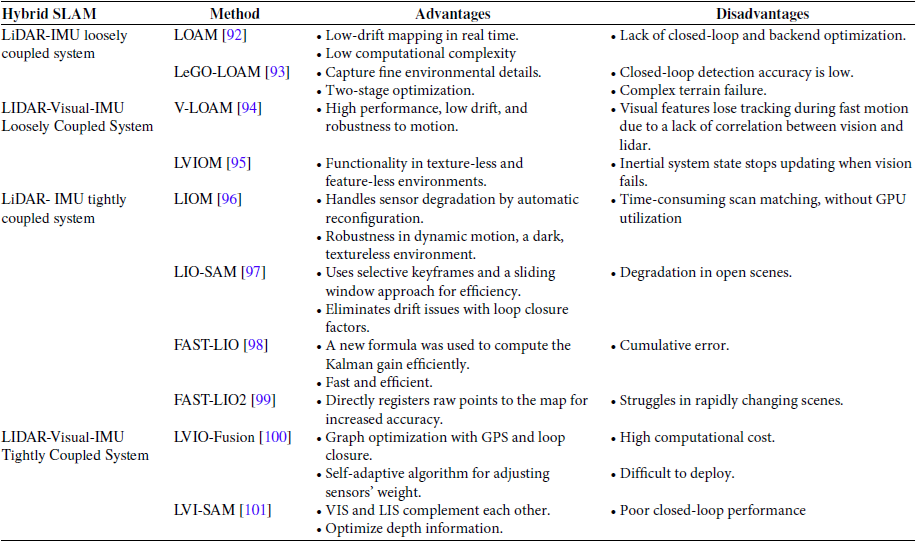
In summary, researchers took a major step forward in hybrid SLAM by developing systems that integrate Lidar, vision, and IMU to work together smoothly, along with additional sensors like wheel/leg odometers and GNSS. Similarly, the increased computational complexity is one of the most challenging problems. In addition, some details need to be optimized, such as dynamic environments, unstructured environments, rain, and snow weather. Table III shows the strengths and weaknesses of each method of hybrid SLAM. The strengths and weaknesses of existing SLAM work are compared in Table III.

Table III. Comparison of existing related work on hybrid SLAM.

2.2.4. Optimization-based approaches

Regarding the final classification, optimization-based approaches formulate localization as an optimization problem, seeking to minimize the discrepancy between predicted and actual sensor measurements. It specifically focuses on pose graph optimization and moving horizon estimation, which optimize over a finite horizon. Optimization-based approaches are divided into post graph-based optimization and moving horizon-based pose estimation for robots.

In graph-based optimization, pose graph techniques use optimization algorithms to refine the robot’s pose estimate by considering constraints and relationships between poses in a graph structure. Moving Horizon Estimation (MHE) is an advanced state estimation technique for localizing mobile robots. MHE solves an optimization problem over a finite time horizon, considering a limited set of past measurements and states, and optimizing within this window to estimate the current state. This approach helps smooth out noise and correct errors. Table IV discusses the advantages and disadvantages of both optimization approaches.

Table IV. Summary of existing methods based on optimization-based approaches.

Pose graph-based optimization

Pose graph-based optimization is a method used in robotics to estimate the robot’s trajectory and pose (position and orientation) within an environment based on sensor measurements and constraints. In this, the environment and the robot’s trajectory are represented as a graph, where each node represents a pose of the robot at a specific point in time, and each edge represents a constraint between two poses. The graph is typically called a “pose graph.” Optimization algorithms, such as Gauss–Newton or Levenberg–Marquardt, adjust the poses in the graph to satisfy all constraints while minimizing overall error. They find the poses that best explain the sensor measurements and constraints.

In ref. [105], a graph-based SLAM algorithm was proposed for indoor dynamic scenarios, consisting of local scan matching and global graph-based optimization. Local scan matching involved preprocessing the LIDAR data, detecting line features, and estimating the rotational and translational values. In contrast, global optimization constructed a topological graph using motion constraints and performed batch optimization to assess the global robot trajectory. A novel method of grid map segmentation for mobile robot global localization using a clustering algorithm and graph representation of clusters was presented in ref. [106]. The technique recovered from incorrect global localization without prior pose information, addressing the “kidnapped robot problem.” An improved method in ref. [107] enhanced mobile robot localization accuracy by combining visual sensors, an IMU, and an odometer through tight coupling and nonlinear optimization. A monocular visual odometer that combined local and global optimization of point-line features to improve self-positioning accuracy in mobile robots was proposed in ref. [108]. The limitations of SLAM using a single sensor were addressed in ref. [109] by combining 2D LiDAR and RGB-D camera data for joint optimization. A grid-based visual localization system was presented in ref. [110], which relied on artificial markers arranged on the ceiling, with the mobile robot capturing images using an up-facing monocular camera. Comparison of two state estimation techniques, particle filters and graph-based localization, was evaluated in the context of automated vehicles [111]. The study discussed the advantages of both algorithms and their ability to adapt to available computational resources at runtime.

Moving horizon estimation

MHE is mathematically formulated as an optimization problem that minimizes the discrepancy between the predicted state (based on the dynamic model) and the measured state (based on sensor data) over a moving time horizon. By integrating sensor measurements with dynamic modeling, MHE enables the robot to determine its global position within an indoor environment, even starting from an unknown location. It does this by continuously updating the localization estimate with new sensor data, allowing the robot to gradually refine its understanding of the environment and accurately locate itself within the global coordinate system.

In ref. [112], the three-dimensional multi-robot cooperative localization problem was addressed by introducing a novel approach based on MHE integrated with EKF for improved localization accuracy. The proposed method bounded localization error, imposed constraints on states and noises, and utilized previous range measurements for current estimation, outperforming traditional EKF-based methods. An ultra-wideband (UWB) localization algorithm for mobile robots presented in ref. [113], which employed a moving horizon optimization, integrating a kinematic model, reference poses, and handling heavy-tailed noise in UWB ranging. Indoor UAV localization is challenging due to the absence of reliable Global Navigation Satellite Systems (GNSS) signals, requiring the development of robust sensor fusion algorithms for state estimation. An adaptive MHE implemented in ref. [114] for indoor UAV localization using ArUco markers, showing improved state estimation performance compared to a high-accuracy motion tracking camera system. According to ref. [115], the focus was on distributed multi-robot SLAM using moving horizon estimation. The algorithm involved sharing sensor measurements and past estimates among robots, and it also utilized the Conjugate/Gradient minimal residual (C/GMRES) method for optimization to enhance computational efficiency. An efficient and versatile multi-sensor fusion framework based on MHE was proposed in ref. [116], emphasizing its capability to handle different sensor characteristics, missing measurements, outliers, and real-time applications. The proposed scheme aimed to improve localization accuracy and robustness, with experimental results demonstrating superior performance compared to the UKF. The accuracy of SLAM using MHE in crowded indoor environments, where measured data may be insufficient, is discussed in ref. [117]. Researchers applied MHE to SLAM to improve motion model evaluation in scenarios with limited data. They conducted experiments comparing MHE-based SLAM with EKF-based SLAM and demonstrated that Sequential Quadratic Programming (SQP) reduced computational complexity.

Symmetrical indoor global localization

This section delves into the problem and key challenge of global localization when a mobile robot encounters a symmetrical indoor environment. Global localization in mobile robotics refers to the process by which a robot determines its position and orientation within an environment without prior knowledge of its starting location. This task becomes particularly challenging in indoor settings due to the absence of GPS signals and the prevalence of symmetrical structures. Symmetrical environments can lead to perceptual aliasing, where different locations appear identical to the robot’s sensors, causing ambiguity in position estimation. For instance, long corridors or repetitive architectural features can mislead the robot into believing it is in multiple possible locations simultaneously. This ambiguity complicates the localization process, as traditional sensors like LiDAR or cameras may not provide distinctive information to disambiguate these positions.

Addressing these challenges is crucial for enhancing the autonomy and efficiency of mobile robots across various applications, such as automated delivery systems, indoor surveillance, and service robotics. This section provides an overview of the complexities involved and outlines the existing efforts aimed at overcoming those obstacles.

3.1. Problem formulation

This paper focuses on the 2-D localization problem, meaning that the robot pose $\mathrm{x}_{t}$ at time step $t\in \mathbb{Z}_{\geq 0}$ is a random variable that satisfies $\mathrm{x}_{t}=[x,y,\theta ]^{T}\in \mathbb{R}^{2}\times \mathbb{S}$ .

Problem 1: Given sensor observations from 2-D laser rangefinder $\mathrm{z}^{\mathbf{L}}$ , control inputs $\mathrm{u}$ , and a pre-built occupancy grid map (OGM) $\mathrm{m}^{\mathrm{L}}$ , the problem of localization in ordinary environments can be formulated as the estimation of robot pose $\mathrm{x}_{t}$ :

(2) \begin{equation}p\left(\mathbf{x}_{t}\mid \mathbf{z}_{1\colon t}^{\mathrm{L}},\mathbf{u}_{1\colon t},\mathbf{m}^{\mathbf{L}}\right)\end{equation}

However, in symmetrical environments, it is tough to match the observations correctly $\mathrm{z}^{\mathbf{L}}$ with OGM $\mathrm{m}^{\mathrm{L}}$ due to the high degree of symmetry in geometric features and low similarity to actual laser measurements. As a result, the robot fails to localize itself in the environment, leading to multiple hypotheses that need to be resolved correctly, as shown in Figure 8. This challenge arises because of symmetry if the environment needs proper attention to improve the localization accuracy of a mobile robot in a symmetrical scenario.

Figure 8. Turtlebot 3 Burger robot platform.

3.2. Key challenges

Global localization for indoor mobile robots can pose a considerable challenge in a symmetrical environment, where the surroundings exhibit significant similarities or mirror-like features, similar rooms, and long corridors. One key challenge is the ambiguity in distinguishing between such similar or symmetrically arranged features. Here are some specific aspects of this challenge:

• • Limited discriminative features: Symmetrical structures may result in a scarcity of discriminative features that can be used for accurate localization. Without unique and easily distinguishable features, the robot may rely on less reliable cues, increasing the likelihood of misjudging its position.

• • Vulnerable to local minima: Symmetrical environments may increase the likelihood of the robot getting stuck in local minima during the global localization process. Ambiguous features may lead the robot to converge on an incorrect position, thinking it has reached the correct location when it has not.

• • Sensor noisy measurements: Sensor noise and inaccuracies can be exacerbated in symmetrical environments, where sensors may provide ambiguous readings due to the presence of similar structures. This noise can lead to inaccuracies in the robot’s perception of its surroundings and contribute to localization errors.

This review paper aims to shed light on the challenges with indoor global localization of mobile robots operating in symmetrical environments. Addressing these key challenges helps to develop an adaptable and sophisticated robotics system capable of effectively navigating through a symmetrical indoor space.

3.3. Review of existing solutions

A review of existing solutions for indoor mobile robot global localization highlights various approaches developed to overcome the challenges of symmetrical environments. Researchers have explored a spectrum of techniques, ranging from traditional methods to state-of-the-art algorithms, to enhance the accuracy and efficiency of localization systems. Table V summarizes existing global localization work in symmetrical indoor environments.

Table V. Summary of global localization in a symmetrical indoor environment.

From the studies listed in Table V, indoor global localization in symmetrical environments presents a complex yet critical challenge for various applications. Despite the inherent difficulties posed by symmetrical features, recent advancements in sensor technologies, machine learning algorithms, and probabilistic methods have shown promising results in improving localization accuracy. However, further research and development are necessary to comprehensively address the unique challenges of symmetrical environments. By leveraging emerging technologies, such as advanced sensor fusion techniques and deep learning algorithms, and exploring innovative hybrid approaches, we can enhance the robustness and accuracy of indoor localization systems in symmetrical environments.

4. Experimental results and discussions

This section presents the evaluation of various global localization algorithms using a benchmarking framework designed for controlled symmetrical environments. The experiments are conducted in two distinct test cases, one with low symmetry and the other with high symmetry, to analyze how different approaches perform under varying levels of structural ambiguity. Comparisons of probabilistic-based, learning-based, SLAM-based, and optimization-based localization methods are undertaken to assess their accuracy, robustness, and computational efficiency. The results highlight the strengths and limitations of each approach, providing insights into their suitability for real-world deployment in symmetrical indoor spaces. Additionally, we discuss the impact of repetitive structures on localization performance and explore potential strategies to enhance robustness in such challenging environments. The findings from this study aim to guide the selection and development of effective localization techniques for applications where symmetry-induced ambiguities pose significant challenges.

4.1. Setup and initialization

To assess the effectiveness of each method in environments with varying levels of symmetry, we utilize the Turtlebot3 Burger robot platform as shown in Figure 8. This platform features a maximum translational velocity of 0.22 m/s and a maximum rotational velocity of 2.84 rad/s. It is equipped with an LDS-01 Laser Distance Sensor, which provides a 360-degree field of view and an IMU. The Turtlebot3 Burger robot is powered by a 32-bit ARM Cortex®-M7 microcontroller unit (MCU) with FPU, running at 216 MHz and delivering 462 DMIPS. Additionally, it incorporates a Single Board Computer (SBC), specifically the Raspberry Pi 3 Model B+.

4.2. Operating scenario

Figure 9 shows the two representative examples of symmetrical environments in experiments, including one low symmetrical square room and one high symmetrical environment with symmetrical rooms

Figure 9. Operating scenarios: (a) low-symmetry square area and (b) high-symmetry area with several symmetrical rooms.

The Hector SLAM algorithm, relying on 2-D LiDAR data, is employed to construct occupancy grid maps of low and high symmetrical environments as shown in Figure 10. Figures 10(a-b) represent low- and high-symmetry environments. Mapping sessions are conducted during the day, with multiple runs performed to select the most accurate representation. Four distinct ground truth poses are manually determined in each scenario using a tape ruler method.

Figure 10. Occupancy grid map for both the cases: (a) low-symmetry environment and (b) high- symmetry environment.

4.3. Comparative analysis

4.3.1. Algorithms for comparison

AMCL, Hector SLAM, Hybrid SLAM, and Cartographer SLAM are commonly used in robotics to test the global localization of mobile robots due to their distinct characteristics and capabilities. Each method has strengths and weaknesses, making it suitable for different scenarios and environments.

AMCL (adaptive Monte Carlo localization)

AMCL uses a particle filter to represent the belief state of a robot’s pose. Particle filters provide a nonparametric representation of the belief or probability distribution over the robot’s pose. This flexibility allows them to handle complex and nonlinear relationships between the robot’s motion and the sensory measurements. Global localization often involves dealing with multimodal distributions, where the true position of the robot is associated with multiple possible poses. Particle filters are well suited for representing and tracking such multimodal distributions, allowing them to capture the uncertainty associated with various possible locations. In Figure 11, AMCL is demonstrated as the robot operating in a symmetrical environment. In Figure 11(a), the robot is initially uncertain about its position, causing the particles to spread throughout a large part of the free space. In Figure 11(b), as the robot moves and approaches a corner of the map, the particles start to converge. Finally, in Figure 11(c), the ambiguity is resolved when the robot is close to its goal, and the robot accurately identifies its position.

Figure 11. Mobile robot localization using AMCL.

Hector SLAM

Hector SLAM relies on scan matching techniques to align successive sensor measurements and build a map of the environment. This method benefits scenarios with low computational resources or limited sensor capabilities. Hector SLAM is known for its real-time performance, making it suitable for applications where low latency is crucial.

Hybrid SLAM

Hybrid SLAM refers to a fusion approach in SLAM that combines different sensor modalities or algorithms to overcome limitations and improve the overall performance of SLAM systems. In a hybrid SLAM system, multiple sensors such as LiDAR, cameras, inertial sensors, and odometry may be integrated, along with various SLAM algorithms, to leverage the strengths of each component. This integration enables more robust and accurate localization and mapping results. This paper uses Hector SLAM with EKF to evaluate the localization performance in both operating scenarios. The EKF provides a mathematical framework incorporating sensor measurements and motion models to estimate the robot’s pose. EKF effectively combines odometry information with sensor measurements (in this paper it is IMU) and Hector SLAM to improve localization accuracy.

Cartographer SLAM

In contrast to Hector SLAM, which is a 2D grid-based SLAM method primarily utilizing LiDAR sensors and recognized for its simplicity, Cartographer employs advanced sensor fusion techniques and global optimization to enhance localization accuracy. While Hector SLAM is appreciated for its user-friendly nature, Cartographer is a more versatile and customizable SLAM library, providing extensive features and configuration options. This increased flexibility often translates into superior localization precision, particularly in environments with complex features and varying lighting conditions.

The rqt_tf_tree of all four algorithms (AMCL, Hector SLAM, Hybrid-SLAM, and Cartographer) used in this paper for comparison are shown in Figures 12– 15. The rqt_tf_tree is a visualization tool in the Robot Operating System (ROS) that helps understand a robotic system’s transform tree (TF) hierarchy. TF is a mechanism in ROS that maintains the relationship between different coordinate frames in the robot’s environment, allowing for seamless coordination between sensors, actuators, and other components. Hence, using rqt_tf_tree helps to understand how sensor data is transformed into a common reference frame, how different robot components are spatially related, and how transformations are propagated through the system. It also helps to identify missing or incorrect TF transforms and debug issues with coordinate frame transformations.

Figure 12. AMCL frame transform hierarchy visualized with rqt_tf_tree.

Figure 13. Hector SLAM frame transform hierarchy visualized with rqt_tf_tree.

Figure 14. Hybrid SLAM frame transform hierarchy visualized with rqt_tf_tree.

Figure 15. Cartographer frame transform hierarchy visualized with rqt_tf_tree.

4.3.2. Performance analysis

When comparing these algorithms as baselines, factors such as accuracy, robustness, computational efficiency, and performance in different environments must be considered. Evaluating these algorithms can help to gain insights into their strengths and limitations, helping to choose the most suitable algorithm for a given robotic application in a symmetrical environment. In this paper, the performance analysis of the above algorithms has been evaluated in the context of global localization of an indoor mobile robot in a symmetrical environment in two cases: (a) low-symmetry environment and (b) high-symmetry environment.

Four distinct locations have been identified within the occupancy grid map illustrated in Figure 11 for assessment purposes. Points P1 and P2 correspond to poses in a lengthy corridor and within one of the symmetrical rooms. Emphasis has been placed on the higher importance of points P1 and P2, as they serve as critical benchmarks for evaluating algorithmic performance in symmetrical environments. However, poses P3 and P4 also hold significance, contributing to the overall global localization performance of the mobile robot. The precise ground truth values for each of the four poses have been determined using the tape and ruler method, and these measurements are detailed in Table VI. For each evaluated approach at each pose, 10 individual random tests were conducted.

Accuracy analysis

The goal of assessing accuracy in robot localization is to evaluate how accurately the robot can estimate its pose. Root mean square error (RMSE) calculates the error between each estimated pose and its corresponding ground truth pose, which is given below:

(3) \begin{equation}\text{RMSE}=\sqrt{\frac{\sum _{i=1}^{N}\,\left(x_{i}-\hat{x}_{i}\right)^{2}}{N}}\end{equation}

where (x_i-x ̂_i) is the error between the estimated pose and the ground truth pose, and n is the total number of measurements. The localization accuracy is shown in Figure 16(a-(b) for both low- and high-symmetry cases. As seen from Figure 16(a), the accuracy of AMCL in determining the poses P1 and P2 is 90% and 89%. The situation worsens as the complexity increases, as in Figure 16(b). Degradation of accuracy happens as AMCL struggles to maintain a diverse set of particles to represent the robot pose accurately. In a symmetrical square environment, the particle diversity is compromised. From Figure 16(b), the AMCL struggles to converge to the correct pose; as a result, accuracy is reduced further to 84%. Meanwhile, utilizing scan matching techniques, Hector SLAM enhances accuracy to 94% in low symmetrical environments 16(a) for poses P1 and P2 by using distinctive features in lidar sensor data to differentiate between various locations. This attribute makes Hector SLAM advantageous in symmetrical structures, enabling the algorithm to adjust to sensor readings’ fluctuations promptly. However, when examining poses P3 and P4 in a high symmetrical environment in Figure 16(b), the accuracy of Hector SLAM is reduced to 89%–90% since the walls in these poses are plain and lack sufficient distinctive features for effective differentiation. Hybrid SLAM, which uses Hector SLAM and EKF for sensor fusion, can potentially handle symmetrical environments more effectively by integrating information from odometry and IMU. This helps to obtain a better pose estimate from both sensor measurements, which improves the localization accuracy of poses to 98%–99%, as depicted in Figure 16(a-b). Combining odometry and IMU in Hybrid SLAM can contribute to more accurate pose estimation, which is beneficial in an environment where symmetrical feature pose challenges other algorithms. Adding to it, the cartographer shows the same range of improvement in localization accuracy for three poses P1, P2, and P3 in both cases as in Figure 16(a-b) due to its advanced sensor fusion and global optimization, making it well suited for improving performance in symmetrical indoor environment.

Table VI. Ground truth value of each pose (m, m, degree).

Robustness analysis

The robustness analysis of the comparison baseline algorithm is evaluated using the correct localization rate (CLR), mismatched localization rate (MLR), and localization failure rate (LFR). These three metrics denote the ratio of successful cases, the ratio of mismatched/misplaced cases, and the ratio of instances where the algorithm fails to localize the robot, over the total number of localization cases, respectively. The sum of CLR, MLR, and LFR must be 100%.

The localization robustness is shown in a stacked histogram in Figure 17, where both low- and high-symmetry cases are represented by Figure 17(a-b), respectively. For low- to high-symmetry environments, the robustness of AMCL degraded to 23.5%. At the same time, other methods like Hector SLAM, Hybrid SLAM, and Cartographer show a decrement in their CLR of 32.52%, 37%, and 42.50%, respectively. The relatively low success rate of all localization methods is attributed to the increased number of similar environments. Therefore, it is evident that the appearance of a symmetrical structure in a complex environment will further lead to deterioration in the performance of AMCL, Hector SLAM, Hybrid SLAM, and Cartographer. This performance degradation shows that the presence of a symmetrical environment is still a challenging problem requiring more research.

Figure 16. Accuracy analysis for: (a) low-symmetry environment and (b) high-symmetry environment.

Computational complexity analysis

The complexity analysis of algorithms is assessed based on CPU usage and processing time. This paper calculates the computational cost of each algorithm’s average processing time to localize the poses. Figure 18(a-b) show the CPU usage of each comparison baseline algorithm.

Figure 17. Robustness analysis of each algorithm in: (a) low symmetrical and (b) high symmetrical environment.

Figure 18. CPU usage of each algorithm for both (a) low and (b) high symmetrical environments.

The symmetrical environment was created at Murdoch University’s Advanced Robotics laboratory with dimensions of 2 m by 3 m. The heightened computational complexity of AMCL in highly symmetrical environments, increasing from 31.5% to 33.5%, is attributed to multiple factors, including the number of particles used to represent potential robot poses (which remains constant at 5000 particles in both environments) and the dimensionality of the state space. On the other hand, the Hybrid SLAM and Cartographer algorithm integrates data from diverse sensors, such as odometry and IMU, and utilizes an EKF. The rise in computational cost for Hybrid SLAM, which is 38.71%, and Cartographer of 44.7% is driven by the intricacy of the sensor fusion process. In comparison, Hector SLAM offers a lower computational complexity of 28% compared to other alternatives.

Therefore, finding a harmonious trade-off between computational cost and the desired accuracy and real-time performance is crucial in the final selection of a localization algorithm for a symmetrical environment robotic application. While learning-based methods offer the potential for high accuracy and adaptability, their computational requirements and the need for extensive training data must also be considered in this balance. For this reason, we do not include learning-based methods in comparison with other algorithms in this paper. However, in future work, we will explore using learning-based methods to address the challenges of symmetrical environments. Additionally, when incorporating learning-based methods, the algorithm evaluation needs to be approached differently to adequately assess their performance and suitability for application in a symmetrical environment, which will be evaluated in the future work of this paper.

5. Discussion and key insights

In the context of global localization for mobile robots operating within symmetrical indoor environments, our study underscores the importance of selecting appropriate localization algorithms to ensure both accuracy and robustness. Traditional methods, such as AMCL, demonstrate adequate performance in environments with low symmetry but encounter significant challenges as environmental complexity and symmetry increase. This decline in performance is primarily due to difficulties in maintaining particle diversity, leading to reduced localization accuracy. These challenges are consistent with findings in recent research, such as [131, 132], where particle filters faced difficulties in environments with high symmetry, particularly in preserving particle diversity.

Conversely, approaches like Hector SLAM, which utilize scan matching techniques, offer improved accuracy by leveraging distinctive features in LiDAR sensor data. However, their effectiveness diminishes in highly symmetrical settings where such distinctive features are scarce. Research in ref. [133] demonstrated that Hector SLAM excels in environments with rich structural features but struggles in scenarios where such features are less pronounced, which aligns with our findings in highly symmetrical environments.

Our findings indicate that Hybrid SLAM and Cartographer, which leverage advanced sensor fusion and global optimization strategies, deliver superior localization performance in symmetrical environments. These approaches integrate data from multiple sensors – such as LiDAR, IMU, and odometry – to enhance pose estimation accuracy. Previous studies [134, 135] have demonstrated that such multi-sensor fusion significantly improves the robustness and precision of localization systems, particularly in complex and highly symmetrical settings. Furthermore, Cartographer, with its use of globally optimized maps, has been shown to perform exceptionally well in environments with intricate geometric structures [136], further emphasizing the effectiveness of global optimization in addressing the challenges posed by symmetry.

Robustness analysis further reveals that, although all evaluated methods exhibit some degradation in performance within highly symmetrical environments, Hybrid SLAM and Cartographer maintain higher levels of robustness compared to AMCL and Hector SLAM. This is attributed to their comprehensive sensor fusion capabilities. As noted in ref. [137], systems relying solely on single-sensor modalities (such as LiDAR or vision) often struggle in environments with repetitive features or minimal texture, highlighting the importance of integrating multiple sensor sources.

In terms of computational complexity, Hybrid SLAM and Cartographer incur higher computational costs due to their intricate sensor fusion mechanisms. While methods like Hector SLAM offer a more computationally efficient alternative, they may not provide the same level of accuracy in highly symmetrical environments. This reinforces the idea with the support of research in ref. [138, 139] that there exists a balance between computational complexity with performance needs, particularly in complex, feature-scarce environments

In conclusion, this study underscores the critical need for advanced sensor fusion and optimization techniques to achieve effective global localization in symmetrical indoor environments. While traditional methods may suffice in less complex settings, the challenges posed by symmetry and environmental complexity necessitate more sophisticated approaches. Future research should focus on refining such methods to balance computational efficiency with localization accuracy and robustness, ensuring reliable performance across a diverse range of indoor environments. Moreover, incorporating learning-based methods into localization strategies presents a promising avenue for addressing the challenges posed by symmetrical environments. For instance, the study in ref. [140] demonstrated that integrating machine learning with probabilistic localization significantly improved performance in environments with repetitive patterns, such as symmetrical indoor spaces.

6. Conclusion

Global localization of mobile robots in symmetrical indoor environments presents significant challenges due to the lack of distinctive features and the inherent ambiguities introduced by uniform structures. This review has comprehensively analyzed various global localization strategies, categorizing them into probabilistic-based, learning-based, SLAM-based, and optimization-based approaches. We have highlighted the strengths, limitations, and practical applicability of these methodologies in real-world scenarios with critical evaluations.

Our findings have indicated that hybrid approaches, which integrate multiple localization techniques, consistently outperform standalone methods in symmetrical environments. Findings from the reviewed literature indicate that combining probabilistic models, learning-based techniques, and SLAM enhances localization accuracy and robustness. Such hybrid methodologies effectively mitigate the challenges posed by symmetry, enabling reliable robot localization in complex indoor settings such as corridors, tunnels, and industrial warehouses.

This review underscores the importance of continued research in hybrid global localization techniques, particularly in developing adaptive frameworks that dynamically switch between strategies based on environmental conditions. Future advancements should focus on enhancing computational efficiency, integrating additional sensor modalities, and addressing real-time implementation constraints. By leveraging the strengths of hybrid approaches, researchers and practitioners can further refine localization systems, paving the way for more autonomous and intelligent robotic navigation in challenging indoor environments.