On the joint right-tail distribution of the forward and backward recurrence times in a delayed renewal process

Abstract

In this paper, we study the joint distribution of the forward and backward recurrence times in a delayed renewal process, as well as their marginal distributions. We obtain several exact results and bounds for these quantities. Some of these bounds are “general,” in the sense that the bounds are valid for any arbitrary distributions of the inter-arrival times, and some are based on aging properties of the distributions of the interarrival times of the renewals. Finally, several numerical examples are presented to illustrate the results.

1. Introduction

Let $\{X_{i}$, $\geq 1\}$ be a sequence of non-negative continuous random variables and $S_{d,n}$ be the partial sums $S_{d,n} = X_{1} + X_{2} + \cdots + X_{n}$, $n \geq 1$, with $S_{d,0} = 0$. Suppose that the random variable $X_{1}$ has distribution function $G(x) = 1 - \overline{G}(x)$ with $G(0) = 0$, and ${\{X}_{i}$, $i \geq 2\}$ constitute a sequence of independent and identically distributed (iid) random variables, independent of $X_{1}$, with common distribution function $F(x) = 1 - \overline{F}(x)$ with $F(0) = 0$. Furthermore, the equilibrium distribution associated with $G$, denoted by $G_e$, is defined as $G_e(t) = \mu_G^{-1} \int_{0}^{t} \overline{G}(y)\,dy,$ and similarly, $F_e(t) = \mu^{-1} \int_{0}^{t} \overline{F}(y)\,dy,$ where $\mu_G = \int_{0}^{\infty} y\, dG(y) \quad \text{and} \quad \mu = \int_{0}^{\infty} y\, dF(y)$ represent the mean interarrival times associated with $G$ and $F$, respectively. If ${0 \leq S}_{d,1} \leq$ $S_{d,2} \leq S_{d,3}$ $\cdots$ denote the times of occurrences of some phenomenon, then $\{S_{d,n},\ n\mathbb{\in N\}}$ is called a delayed or modified renewal process. The $S_{d,n}$ are called the renewals or the epochs of the delayed renewal process, and $X_{n} = S_{d,n} - S_{d,n - 1}$, $n \geq 1$, are the interarrival or waiting times of renewals.

With each delayed renewal process, we can associate the stochastic process $\{N_{d}(t),t \geq 0\}$, continuous in time, with values in $\mathbb{N}$, defined by $N_{d}(t) = \sup\left\{n\mathbb{\in N\ :\ }S_{d,n} \leq t \right\}$ if $X_{1} \leq t$, to be the number of renewals in $\lbrack 0,\ t\rbrack$ with $N(t) = 0$, if $X_{1} \gt t$. Then, $N_{d}(t)$ is called the associated counting process or the delayed renewal counting process and represents the total number of renewals on $(0,\ t\rbrack$, and it holds true that

\begin{equation*}\Pr\left( N_{d}(t) \geq n\right) = \Pr(S_{d,n} \leq t)) = \left( G*F^{(n - 1)} \right)(t),\end{equation*}

and

\begin{equation*}\Pr\left( N_{d}(t) = n\right) = \left( G*F^{(n - 1)} \right)(t) - \left(G*F^{(n)} \right)(t),\end{equation*}

where $F^{(n)}$ denotes the n-fold Lebesgue–Stieltjes convolution product of the distribution function F with itself. We recall that the Lebesgue–Stieltjes-type convolution of functions $g\ :\lbrack 0,\ \infty) \rightarrow \mathbb{R}$ and $F$ will be denoted by $g*F$ and is defined as $(g*F)(x) = \int_{0}^{x}{g(x - y)dF(y)}$. 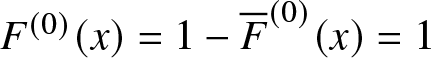For any $n = 1,\ 2,\ 3,\ \cdots$, by $F^{(n)}(x) = 1 - {\overline{F}}^{(n)}(x)$ we shall denote the $n -$ fold convolution of the distribution function $F$, defined by $F^{(n)}(x) = (F^{(n - 1)}*F)(x)$, with $F^{(0)}(x) = 1 - {\overline{F}}^{(0)}(x) = 1$ for $x \geq 0$, $F^{(0)}(x) = 1 - {\overline{F}}^{(0)}(x) = 0$ for $x \lt 0$ and $F^{(1)}(x) = F(x)$.

A primary quantity of interest is the delayed or modified renewal function, which is defined as $M_{d}(t) = E\lbrack N_{d}(t)\rbrack$. The function $M_{d}(t)$ represents the expected number of renewals in $\lbrack 0,\ t\rbrack$ for $t \in \lbrack 0,\ \infty)$ and it is well known (see, e.g., Karling and Taylor [13] p. 198) that $M_{d}(t)$ satisfies the following renewal equation

\begin{equation*} M_{d}(t) = \sum_{n = 1}^{\infty}{\left( G*F^{(n - 1)} \right)(t) = \sum_{n = 0}^{\infty}{\left( G*F^{(n)} \right)(t)}} \end{equation*}

From the above equation, it follows (e.g., Resnick [20], Section 3.5) that the delayed renewal function $M_{d}$ satisfies the renewal-type equation

\begin{equation*}M_{d}(t) = A(t) + \int_{0}^{t}{M_{d}(t - y)dF(y)}, ~t \geq 0. \end{equation*}

There are many practical situations where the delayed renewal process can be used to model several physical phenomena (see, e.g., Pekalp et al. [19] and Chadjiconstantinidis [4]). For example, let us consider an item, say an electric bulb, that fails at times $S_{d,0}$, $S_{d,1}$, $S_{d,2}$, $\cdots$, and is replaced at the time of failure by anew item on the same sort. Then $F$ is the distribution of the lifetime of an item. If the item present at time $x = 0$ is not new, then its lifetime distribution need not have distribution $F$. Another example is the following. The first engine used in vehicle generally lasts longer than renewals (where the renewal might be the same engine after being reconditioned).

Analytical solutions of the delayed renewal function are possible only for a very few lifetime distributions of the inter-arrival times. See, for example, Pekalp et al. [19], who obtained an exact formula for $M_{d}(x)$ when $G$ is an exponential distribution and $F$ is an exponential (with different parameter) and/or an Erlang ( $2$) distribution. In the same paper, the authors obtained parametric plug-in estimators for the delayed renewal function and the variance of the delayed renewal counting process. In general, if the distributions of $X_{1}$ and $X_{i}$, $i \geq 2$ belong to the rational family of distributions (e.g., if they have phase-type distributions), then we can obtain $M_{d}(x)$ analytically. For other distributions of the inter-arrival times, the delayed renewal equation on the one hand usually do not have analytical solutions, and on the other hand, it is very difficult and complicated to obtain such solutions. For this reason, alternate approaches, such as bounds for $M_{d}(t)$ have been developed (see, e.g., Chadjiconsatntinidis ([4], [5])).

If $X_{1} \triangleq X_{i}$ for any $i \geq 2$, the symbol $\triangleq$ means equality in distribution, that is, if ${\{X}_{i}$, $i \geq 1\}$ is a sequence of iid random variables, then $G(t) = F(t)$ and in this case $S_{d,n}$ will usually denoted by $S_{n}$, and $N_{d}(t)$ by $N(t)$. Then $\{S_{n},\ n\mathbb{\in N\}}$ is called the ordinary renewal process and $\{N(t),\ t \gt 0\}$ the ordinary renewal counting process. Hence, $M_{d}(t)$ is reduced to the ordinary renewal function denoted by $M(t)$, and is defined by 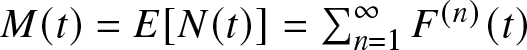$M(t) = E\lbrack N(t)\rbrack = \sum_{n = 1}^{\infty}{F^{(n)}(t)}$. Therefore, the delayed or modified renewal process differs from an ordinary renewal process in that the distribution of $X_{1}$ is different from that of subsequent $X_{i}$, $i \geq 2$, that is, if the first arrival time $X_{1}$ is allowed to have a different distribution than the other inter-arrival times $\left\{X_{2},\ {\ X}_{3},\ \cdots \right\}$ then we obtain the delayed or modified renewal process. However, in many cases, if not all interarrival times have the same distribution is more realistic. For this reason, in this paper, we study some quantities related to the delayed renewal process.

Apart from the delayed renewal function, two other quantities of primary interest in renewal theory are the forward and backward recurrence times. The backward recurrence time, also known as the age at time  $t$, will be denoted by  $\delta_{t}^{d}$ and is defined by 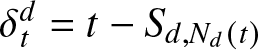 $\delta_{t}^{d} = t - S_{d,N_{d}(t)}$. It represents the time that has elapsed since the last renewal. The forward recurrence time at time  $t$, denoted by  $\gamma_{t}^{d}$, is defined by 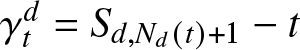 $\gamma_{t}^{d} = S_{d,N_{d}(t) + 1} - t$ and corresponds to the length of time from  $t$ until the occurrence of the next renewal. It is also called residual lifetime, and it occurs frequently in various stochastic models, such as in reliability, queueing, or inventory theory. For several applications of these quantities, see in Chadjiconstantinidis and Politis [6] and the references therein.

The forward and backward recurrence times in an ordinary renewal process have been studied, and various results are available (see, e.g., Karlin and Taylor [13], Gupta [11], Gakis and Sivazlian ([9],[10]), and most recently Losidis and Politis [16], Losidis ([14], [15]), Losidis et al. ([17], [18])) and Chadjiconsatntinidis and Politis ([6]). Karling and Taylor [13] and Janssen and Manca [12] offer some results for the survival function of the forward recurrence time $\gamma_{t}^{d}$. These are the only known results in the literature concerning quantities related to the delayed forward and/or backward recurrence times.

So, in this paper, the focus is on the joint and marginal distributions of $\gamma_{t}^{d}$ and $\delta_{t}^{d}$. To the best of our knowledge, results for the joint distribution of $\gamma_{t}^{d}$ and $\delta_{t}^{d}$ are presented for the first time in this paper. In more detail, we study the joint distribution of the forward and backward recurrence times $\gamma_{t}^{d}$, $\delta_{t}^{d}$, and we obtain exact results as well as bounds for the right tails of those quantities. As a result, we obtain exact results for the marginal distributions of $\gamma_{t}^{d}$, $\delta_{t}^{d}$ and bounds for their right tail probabilities.

We assume throughout this paper that the distribution functions F and G are absolutely continuous with densities f and g respectively, so that $M(t)$ and $M_{d}(t)$ also have densities which are denoted by $m(t)$ and $m_{d}(t)$, and are called the renewal densities of an ordinary and a delayed renewal process.

For a distribution function $V$, we write $\overline{V} = 1 - V$ for the associated tail function. We shall use the following well-known aging classes of distributions on the nonnegative half-line. A distribution $V$ is said to have an increasing failure rate (IFR) if $log\ V$ is concave, that is, for all $x \geq 0$, the function $\overline{V}(t + x)\text{/}\overline{V}(t)$ is decreasing in t for all t such that $\overline{V}(t) \geq 0$. Similarly, if $log\ V$ is convex, then $V$ is called a decreasing failure rate (decreasing failure rate) distribution. Next, a distribution $V$ is called new better than used (new better than used) if $\overline{V}(t + x) \leq \overline{V}(t)\overline{V}(x)$ for all $x,t \geq 0$, while $V$ is called new worse than used (new worse than used) if $\overline{V}(t + x) \geq \overline{V}(t)\overline{V}(x)$ for all $x,t \geq 0$. It is known that the decreasing failure rate (IFR) is a subclass of the new worse than used (resp., new better than used) class of distributions. Further details on these and other aging classes of distributions can be found in the books of Shaked and Shanthikumar [21] and Willmot and Lin [22].

The paper is organized as follows: In the next section, we demonstrate why the joint distribution of the forward and backward recurrence times and their marginal tails is essential using examples from real-life applications. In Section 3, we obtain exact results for the right tail $\Pr(\delta_{t}^{d} \geq x,\ \gamma_{t}^{d} \gt y)$ of the joint distribution of the forward and backward recurrence times $\gamma_{t}^{d}$ and $\delta_{t}^{d}$, as well as for their marginal tails $\Pr(\delta_{t}^{d} \geq x)$ and $\Pr(\gamma_{t}^{d} \gt y)$. Also, several general bounds are obtained for all these quantities, as well as bounds which are based on several aging classes of the distributions of the interarrival times and bounds based on the delayed renewal density. Finally, in Section 4, we give several numerical examples to illustrate our results.

2. Applications of the backward and forward recurrence times

Renewal theory, particularly the analysis of forward and backward recurrence times, plays a crucial role in various real-time applications such as healthcare, reliability engineering, and queueing systems. These applications depend not only on average behavior but also on the tail properties of recurrence time distributions, which can reveal rare but critical scenarios. The ability to model and respond to such temporal uncertainty makes renewal theory a powerful and versatile framework in time-sensitive environments.

In this section, we present an example from the aviation industry, where operational reliability and safety are vital. Predictive maintenance is critical in minimizing risks and optimizing aircraft availability. Renewal theory can be applied to model the timing of past and future maintenance events by analyzing the backward recurrence time (time since the last maintenance) and the forward recurrence time (time until the next maintenance).

In this context, the joint tail behavior of the backward and forward recurrence times provides insight into situations where both times are large, identifying potential high-risk periods of system degradation or unexpected failure. Such analysis supports condition-based maintenance strategies, where service decisions depend on actual operating conditions and event timing rather than fixed schedules.

In practical applications such as aviation maintenance, the assumptions of the ordinary renewal process—that all inter-arrival times, including the first, are identically distributed may not hold. Often, aircraft enter observation or service at arbitrary points in their operational cycle. The delayed renewal process offers a more appropriate framework, allowing the first inter-arrival time to follow a different distribution, thereby capturing more realistic operational dynamics.

3. The joint distribution of the forward and backward recurrence times

Let ${\overline{W}}_{t}^{d}(x,y) = \Pr(\delta_{t}^{d} \geq x,\ \gamma_{t}^{d} \gt y)$, $0 \leq x \leq t$, $y \geq 0$, be the joint survival function (joint right-tail) of the random variables $\gamma_{t}^{d}$ and $\delta_{t}^{d}$. In this notation, we have used $\delta_{t}^{d} \geq x$ rather than $\delta_{t}^{d} \gt x$ for notational convenience and since the distribution of $\delta_{t}^{d}$ possesses a point mass at $t$, so that our results remain valid without change for $x = t$. Our first result concerns a formula for computing the joint right-tail of the random variables $\gamma_{t}^{d}$ and $\delta_{t}^{d}$.

Proposition 1. For any $0 \leq x \leq t$ and $y \geq 0$, the joint right-tail of $\gamma_{t}^{d}$ and $\delta_{t}^{d}$ is given by

(1)\begin{equation} {\overline{W}}_{t}^{d}(x,y) = \overline{G}(t + y) + \int_{0}^{t - x}{\overline{F}(t + y - s)dM_{d}(s)} \end{equation}

Proof. We have

\begin{align*} {\overline{W}}_{t}^{d}(x,y) &= \sum_{n = 1}^{\infty}\Pr\left( S_{n - 1} \leq t - x,S_{n} \geq t + y \right)\\ &= \Pr\left( X_{1} \gt t + y \right) + \sum_{n = 2}^{\infty}{\int_{0}^{t - x}{\Pr\left( X_{n} \gt t + y - s \right)d\left( \Pr\left( \sum_{i = 1}^{n - 1}X_{i} \leq s \right) \right)}}\\ &= \overline{G}(t + y) + \int_{0}^{t - x}{\Pr\left( X_{n} \gt t + y - s \right)d\sum_{n = 2}^{\infty}G}*F^{(n - 2)}(s)\\ &= \overline{G}(t + y) + \int_{0}^{t - x}{\overline{F}(t + y - s)dM_{d}(s)}. \end{align*}

Therefore, if there exists an exact formula for the delayed renewal function $M_{d}(t)$, one can use Proposition 1 to obtain an exact representation for ${\overline{W}}_{t}^{d}(x,y)$ as well. For example, Chadjiconstantinidis [5] proved that if the random variable $X_{1}$ follows an exponential distribution with parameter $\lambda_{1} \gt 0$, and the i.i.d. random variables $X_{i}$, $i \geq 2$ have also an exponential distribution with parameter $\lambda_{2} \gt 0$ with $\lambda_{1} \neq \lambda_{2}$, then

\begin{equation*}M_{d}(t) = \frac{\lambda_{1} - \lambda_{2}}{\lambda_{1}} + \lambda_{2}t + \frac{\lambda_{2} - \lambda_{1}}{\lambda_{1}}e^{- \lambda_{1}t},~ t \geq 0.\end{equation*}

Therefore, using Proposition 1, we get the following exact formula for ${\overline{W}}_{t}^{d}(x,y)$

\begin{equation*}{\overline{W}}_{t}^{d}(x,y) = e^{- \lambda_{1}(t + y)} + \left\lbrack 1 - e^{- \lambda_{1}(t - x)} \right\rbrack e^{- \lambda_{2}(x + y)}, 0 \leq x \leq t, y \geq 0.\end{equation*}

Another representation for the evaluation of ${\overline{W}}_{t}^{d}(x,y)$ is given in the following.

Proposition 2. For any $0 \leq x \leq t$ and $y \geq 0$, it holds that

(2)\begin{equation} {\overline{W}}_{t}^{d}(x,y) = 1 - M_{d}(t + y) + M_{d}(t - x)\overline{F}(x + y) + \int_{0}^{x + y}{M_{d}(t + y - s)dF(s)}. \end{equation}

Proof. First, we calculate the integral $\int_{0}^{x}{M_{G}(t - s)dF(s)}$ as follows:

\begin{align*} \int_{0}^{x}{M_{G}(t - s)dF(s)} &= M_{G}(t) - M_{G}(t - x)\overline{F}(x) - \int_{0}^{x}{m_{G}(t - s)\overline{F}(s)ds}\\ &= M_{G}(t) - M_{G}(t - x)\overline{F}(x) - \int_{t - x}^{t}{\overline{F}(t - s)dM_{G}(s)}. \end{align*}

Setting $y = 0$ into (1), yields that

\begin{equation*}\overline{G}(t) + \int_{0}^{t - x}{\overline{F}(t - s)dM_{G}(s)} + \int_{t - x}^{t}{\overline{F}(t - s)dM_{G}(s)} = 1,\end{equation*}

and then

\begin{equation*}\int_{0}^{x}{M_{G}(t - s)dF(s)} = M_{G}(t) - M_{G}(t - x)\overline{F}(x) - G(t) + \int_{0}^{t - x}{\overline{F}(t - s)dM_{G}(s)}.\end{equation*}

Setting $x = x + y$ and $t = t + y$ into the above gives:

\begin{align*} \int_{0}^{t - x}{\overline{F}(t + y - s)dM_{G}(s)} &=G(t + y) + M_{G}(t + y) - M_{G}(t - x)\overline{F}(x + y)\\ &+ \int_{0}^{x + y}{M_{G}(t + y - s)dF(s)}. \end{align*}

Inserting the last equation into (1) completes the proof.

The results in Propositions 1 and 2 are also useful to obtain bounds for the joint right-tail 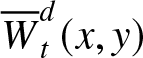${\overline{W}}_{t}^{d}(x,y)$. A general two-sided bound in terms of the delayed renewal function $M_{d}(t)$ is given in the following.

Theorem 1. For any $0 \leq x \leq t$ and $y \geq 0$, it holds

(3)\begin{equation} \overline{G}(t + y) + \overline{F}(t + y)M_{d}(t - x) \leq {\overline{W}}_{t}^{d}(x,y) \leq 1 - \left\lbrack M_{d}(t + y) - M_{d}(t - x) \right\rbrack\overline{F}(x + y). \end{equation}

Proof. For $0 \leq s \leq t - x$ we have $t + y - s \leq t + y$ and since $\overline{F}(x)$ is a decreasing function in $x$, it holds $\overline{F}(t + y - s) \geq \overline{F}(t + y)$, and hence from Proposition 1, we get

\begin{equation*}{\overline{W}}_{t}^{d}(x,y) \geq \overline{G}(t + y) + \overline{F}(t + y)\int_{0}^{t - x}{dM_{d}(s)},\end{equation*}

and the lower bound in (3) follows immediately.

Also, for $s \geq 0$ since the delayed renewal function $M_{d})(t)$ is a non-decreasing function in $t \geq 0$, it holds $M_{d}(t + y - s) \leq M_{d}(t + y)$ and hence from Proposition 2 we obtain

\begin{align*} {\overline{W}}_{t}^{d}(x,y) &\leq 1 - M_{d}(t + y) + M_{d}(t - x)\overline{F}(x + y) + M_{d}(t + y)\int_{0}^{x + y}{dF(s)}\\ &= 1 - M_{d}(t + y) + M_{d}(t - x)\overline{F}(x + y) + M_{d}(t + y)F(x + y)\\ &= 1 - M_{d}(t + y)\overline{F}(x + y) + M_{d}(t - x)\overline{F}(x + y). \end{align*}

The usefulness of the bounds given in (3) is that we can use suitable known lower and upper bounds for $M_{d}(t)$ by inserting them into (3) to obtain bounds for ${\overline{W}}_{t}^{d}(x,y)$, provided that the resulting bounds lie in the interval [0, 1]. In particular, one can use only lower bounds for $M_{d}(t)$, say $A(t)$, in order to obtain lower bounds for ${\overline{W}}_{t}^{d}(x,y)$, provided that $A(t - x) \leq \frac{G(t + y)}{\overline{F}(t + y)}$, for $0 \leq x \leq t$, $y \geq 0$. Also, one can find lower bounds for the difference $M_{d}(t + y) - M_{d}(t - x)$, say $B_{t}(x,y)$, in order to obtain upper bounds for ${\overline{W}}_{t}^{d}(x,y)$, provided that 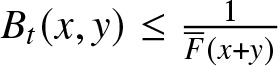$B_{t}(x,y) \leq \frac{1}{\overline{F}(x + y)}$, for $0 \leq x \leq t$, $y \geq 0$. For example, Chadjiconstantinidis [5] obtained the following lower bound for $M_{d}(t)$

(4)\begin{equation} M_{d}(t) \geq \frac{t - \mu_{G}G_{e}(t)}{\mu F_{e}(t)}, t \geq 0, \end{equation}

provided that $0 \lt \mu \lt \infty$, ${0 \lt \mu}_{G} \lt \infty$. Inserting the above bound into the lower bound of (3), we obtain immediately

\begin{equation*}{\overline{W}}_{t}^{d}(x,y) \geq \overline{G}(t + y) + \frac{t - x - \mu_{G}G_{e}(t - x)}{\mu F_{e}(t - x)}\overline{F}(t + y), 0 \leq x \leq t \textit{, } y \geq 0.\end{equation*}

Chadjiconstantinidis [5] also obtained the following upper bound for the delayed renewal function

\begin{equation*}M_{d}(t) \leq U(t) - \frac{\mu_{G}}{\mu} \frac{G_{e}(t)}{F_{e}(t)},~ t \geq 0\end{equation*}

and combining this with the famous Lorden’s upper bound for $U(t)$, namely

\begin{equation*}U(t) \leq \frac{t}{\mu} + \frac{\mu_{2}}{\mu^{2}},\end{equation*}

we get

(5)\begin{equation} M_{d}(t) \leq \frac{t}{\mu} + \frac{\mu_{2}}{\mu^{2}} - \frac{\mu_{G}}{\mu} \frac{G_{e}(t)}{F_{e}(t)},~ t \geq 0. \end{equation}

A weaker but simpler bound than that given by (4) is

\begin{equation*}M_{d}(t) \geq \frac{t - \mu_{G}}{\mu},~ t \geq 0.\end{equation*}

Now, using this and (5) we obtain

\begin{align*} M_{d}(t + y) - M_{d}(t - x) &\geq \frac{t + y - \mu_{G}}{\mu} - \frac{t - x}{\mu} - \frac{\mu_{2}}{\mu^{2}} + \frac{\mu_{G}}{\mu} \frac{G_{e}(t - x)}{F_{e}(t - x)}\\ &=\frac{x + y}{\mu} - \frac{\mu_{2}}{\mu^{2}} - \frac{\mu_{G}}{\mu}\left\lbrack 1 - \frac{G_{e}(t - x)}{F_{e}(t - x)} \right\rbrack, \end{align*}

and inserting this lower bound into the RHS of (3), we get

\begin{equation*}{\overline{W}}_{t}^{d}(x,y) \leq 1 - \left\{\frac{x + y}{\mu} - \frac{\mu_{2}}{\mu^{2}} - \frac{\mu_{G}}{\mu}\left\lbrack 1 - \frac{G_{e}(t - x)}{F_{e}(t - x)} \right\rbrack \right\}\overline{F}(x + y).\end{equation*}

Similarly, one can use several upper and lower bounds for $M_{d}(t)$ and the difference $M_{d}(t + x) - M_{d}(t)$ obtained by Chadjiconstantinidis ([4], [5]) to obtain bounds for the joint right-tail ${\overline{W}}_{t}^{d}(x,y)$ by using Theorem 1. The details are omitted.

By letting $x = 0$ and $y = 0$ in (1) and (2), we get formulae for the evaluation of the right-tail distribution of the marginal random variables $\gamma_{t}^{d}$ and $\delta_{t}^{d}$, respectively. Hence, we have the following

Corollary 1. (i) For any $y \geq 0$ it holds

(6)\begin{equation} \Pr\left( \gamma_{t}^{d} \gt y \right) = \overline{G}(t + y) + \int_{0}^{t}{\overline{F}(t + y - s)dM_{d}(s)}, \end{equation}

and

(7)\begin{equation} \Pr\left( \gamma_{t}^{d} \gt y \right) = 1 - M_{d}(t + y) + M_{d}(t)\overline{F}(y) + \int_{0}^{y}{M_{d}(t + y - s)dF(s)}. \end{equation}

(ii) For any $0 \leq x \leq t$ it holds

(8)\begin{equation} \Pr\left( \delta_{t}^{d} \geq x \right) = \overline{G}(t) + \int_{0}^{t - x}{\overline{F}(t - s)dM_{d}(s)}, \end{equation}

and

(9)\begin{equation} \Pr\left( \delta_{t}^{d} \geq x \right) = 1 - M_{d}(t) + M_{d}(t - x)\overline{F}(x) + \int_{0}^{x}{M_{d}(t - s)dF(s)}. \end{equation}

Using Theorem 1 (and or Corollary 1 by employing similar arguments as in Theorem 1), we directly obtain two-sided bounds for $\Pr\left( \gamma_{t}^{d} \gt y \right)$ and $\Pr\left( \delta_{t}^{d} \geq x \right)$. Thus, we have the following

Corollary 2. (i) For any $y \geq 0$ it holds

\begin{equation*}\overline{G}(t + y) + \overline{F}(t + y)M_{d}(t) \leq \Pr\left( \gamma_{t}^{d} \gt y \right) \leq 1 - \left\lbrack M_{d}(t + y) - M_{d}(t) \right\rbrack\overline{F}(y).\end{equation*}

(ii) For any $0 \leq x \leq t$ it holds

\begin{equation*}\overline{G}(t) + \overline{F}(t)M_{d}(t - x) \leq \Pr\left( \delta_{t}^{d} \geq x \right) \leq 1 - \left\lbrack M_{d}(t) - M_{d}(t - x) \right\rbrack\overline{F}(x).\end{equation*}

Therefore, as previously one can use known upper and lower bounds for $M_{d}$ to obtain bounds for the right-tails $\Pr\left( \gamma_{t}^{d} \gt y \right)$ and $\Pr\left( \delta_{t}^{d} \geq x \right)$.

In an ordinary renewal process, Chen [7] proves that if the forward recurrence time is stochastically decreasing (increasing) in $t \geq 0$, then the distribution of the inter-arrival times is new better than used (new worse than used). In the following result, we show that the stochastic decrease (increase) of the $\gamma_{t}^{d}$ is linked with the new better than used (new worse than used) class for the distribution of the first inter-arrival time.

Proposition 3. If $\gamma_{t}^{d}$ is stochastically decreasing (increasing) in $t \geq 0$, then the distribution function $G$ of the first inter-arrival time is new better than used (new worse than used).

Proof. Karlin and Taylor ([13], p. 200) proved that

\begin{equation*}\Pr\left( \gamma_{t}^{d} \gt y \right) = \overline{G}(t + y) + \int_{0}^{t}{\Pr\left( \gamma_{t - s}^{d} \gt y \right)dG(s)}.\end{equation*}

Assuming that $\gamma_{t}^{d}$ is stochastically decreasing (increasing) in $t \geq 0$, since for $0 \leq s \leq t$ we also have $0 \leq t - s \leq t$, then it holds $\Pr{\left( \gamma_{t - s}^{d} \gt y \right) \geq ( \leq )}\Pr\left( \gamma_{t}^{d} \gt y \right)$ and hence from the above equation, we get

\begin{align*} \Pr\left( \gamma_{t}^{d} \gt y \right) &\geq ( \leq )\overline{G}(t + y) + \int_{0}^{t}{\Pr\left( \gamma_{t}^{d} \gt y \right)dG(s)}\\ & = \overline{G}(t + y) + \Pr\left( \gamma_{t}^{d} \gt y \right)G(t), \end{align*}

implying that

(10)\begin{equation} \Pr\left( \gamma_{t}^{d} \gt y \right)\overline{G}(t) \geq ( \leq )\overline{G}(t + y). \end{equation}

Also, for $t \geq 0$ it holds $\Pr\left( \gamma_{0}^{d} \gt y \right) \geq ( \leq )\Pr\left( \gamma_{t}^{d} \gt y \right)$. By letting $t = 0$ in (3) it follows that $\Pr{\left( \gamma_{0}^{d} \gt y \right) = \overline{G}(y)}$, and thus it holds $\overline{G}(y) \geq ( \leq )\Pr\left( \gamma_{t}^{d} \gt y \right)$, Therefore, from (10) we get that $\overline{G}(t + y) \leq ( \geq )\overline{G}(t)\overline{G}(y)$, implying that the distribution function $G$ is new better than used (new worse than used).

3.1. Right-tail bounds for recurrence times under aging properties

In this subsection, we shall give bounds for the joint right-tail 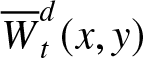${\overline{W}}_{t}^{d}(x,y)$ as well as for 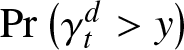$\Pr\left( \gamma_{t}^{d} \gt y \right)$ and $\Pr\left( \delta_{t}^{d} \geq x \right)$ which are based on several reliability classes of the common distribution function $F$ of $\{X_{i}$, $i \geq 2\}$. Our first bound for 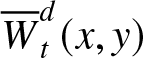${\overline{W}}_{t}^{d}(x,y)$ is expressed in terms of the right-tail probability of the backward recurrence time.

Corollary 3. If the distribution function $F$ is new worse than used (new better than used), then

(11)\begin{equation} {\overline{W}}_{t}^{d}(x,y) \geq ( \leq )\overline{G}(t + y) - \overline{F}(y)\overline{G}(t) + \overline{F}(y)\Pr\left( \delta_{t}^{d} \geq x \right), \end{equation}

and

(12)\begin{equation} \Pr{\left( \gamma_{t}^{d} \gt y \right) \geq ( \leq )\overline{G}(t + y) + \overline{F}(y)G(t)}. \end{equation}

Proof. If the distribution function $F$ is new worse than used (new better than used), then for $0 \leq s \leq t - x \leq t$, it holds $\overline{F}(t + y - s) \geq ( \leq )\overline{F}(y)\overline{F}(t - s)$, and hence from (1) and (8) we get

\begin{align*} {\overline{W}}_{t}^{d}(x,y) &\geq ( \leq )\overline{G}(t + y) + \overline{F}(y)\int_{0}^{t - x}{\overline{F}(t - s)dM_{d}(s)}\\ &= \overline{G}(t + y) + \overline{F}(y)\left\lbrack \Pr\left( \delta_{t}^{d} \geq x \right) - \overline{G}(t) \right\rbrack, \end{align*}

which gives the bound in (11).By letting $x = 0$ in (11) we immediately obtain the bound in (12).

By letting $y = 0$ in we get (11) that $\Pr{\left( \delta_{t}^{d} \geq x \right) \geq ( \leq )\overline{G}(t)}$ for all $0 \leq x \leq t$, if the distribution function $F$ is new worse than used (new better than used).

In the following, we give an upper (lower) bound for 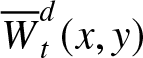${\overline{W}}_{t}^{d}(x,y)$ in terms of the delayed renewal function $M_{d}$, under the same assumption that the interarrival distribution $F$ is new better than used (new worse than used). It should be noted that an upper bound for ${\overline{W}}_{t}^{d}(x,y)$ when the distribution function $F$ is new worse than used, will be given in Corollary 9 below.

Proposition 4. Let $0 \leq x \leq t$ and $y \geq 0$.

(i) If the distribution function $F$ is new better than used, then

\begin{equation*}{\overline{W}}_{t}^{d}(x,y) \leq \overline{G}(t + y) + \overline{F}(y)\left\{G(t) + \left\lbrack M_{d}(t - x) - M_{d}(t) \right\rbrack\overline{F}(x) \right\}.\end{equation*}

(ii) If the $F$ is new worse than used, then

\begin{equation*}{\overline{W}}_{t}^{d}(x,y) \geq \overline{G}(t + y) + \overline{F}(y)\left\{G(t) + M_{d}(t - x) - M_{d}(t) \right\}.\end{equation*}

Proof. (i) It holds

(13)\begin{align} \int_{0}^{t - x}{\overline{F}(t + y - s)dM_{d}(s)} &\leq \overline{F}(y)\int_{0}^{t - x}{\overline{F}(t - s)dM_{d}(s)}\cr &= \overline{F}(y)\left\{\overline{F}(x)M_{d}(t - x) - \int_{0}^{t - x}{f(t - s)M_{d}(s)ds} \right\}\cr &= \overline{F}(y)\left\{\overline{F}(x)M_{d}(t - x) - \int_{x}^{t}{M_{d}(t - s)dF(s)} \right\}\cr &= \overline{F}(y)\left\{\overline{F}(x)M_{d}(t - x) - \int_{0}^{t}{M_{d}(t - s)dF(s)} \right.\cr &\left. \quad + \int_{0}^{x}{M_{d}(t - s)dF(s)} \right\}\cr &= \overline{F}(y)\left\{\overline{F}(x)M_{d}(t - x) + G(t) - M_{d}(t) \right.\ \cr &\left. \quad + \int_{0}^{x}{M_{d}(t - s)dF(s)} \right\} \end{align}

Since for $0 \leq s \leq x \leq t$, we have $t - x \leq t - s \leq t$, implying that $M_{d}(t - x) \leq M_{d}(t - s) \leq M_{d}(t)$, from (10) we get

\begin{align*} \int_{0}^{t - x}{\overline{F}(t + y - s)dM_{d}(s)} &\leq \overline{F}(y)\left\{\overline{F}(x)M_{d}(t - x) + G(t) - M_{d}(t) + M_{d}(t)\int_{0}^{x}{dF(s)} \right\}\\ &= \overline{F}(y)\left\{\overline{F}(x)M_{d}(t - x) + G(t) - \overline{F}(x)M_{d}(t) \right\}\\ &= \overline{F}(y)\left\{G(t) + \left\lbrack M_{d}(t - x) - M_{d}(t) \right\rbrack\overline{F}(x) \right\}, \end{align*}

and hence the result follows from (1).

(ii) If the distribution function $F$ is new worse than used, then as in (10) we get that

\begin{align*} \int_{0}^{t - x}{\overline{F}(t + y - s)dM_{d}(s)} &\geq \overline{F}(y)\left\{\overline{F}(x)M_{d}(t - x) + G(t) - M_{d}(t)+ \int_{0}^{x}{M_{d}(t - s)dF(s)} \right\}\\ &\geq \overline{F}(y)\left\{\overline{F}(x)M_{d}(t - x) + G(t) - M_{d}(t) + M_{d}(t - x)\int_{0}^{x}{dF(s)} \right\}\\ &= \overline{F}(y)\left\{G(t) + M_{d}(t - x) - M_{d}(t) \right\}, \end{align*}

and thus, again from (1) we obtain the required lower bound.

By letting $x = 0$ in the bounds of Proposition 4, we reveal the result in (12). Also, by letting $y = 0$ in the bounds of Proposition 4, we get the following

Corollary 4. For any $0 \leq x \leq t$, if the distribution function $F$ is new better than used, then

\begin{equation*}\Pr\left( \delta_{t}^{d} \geq x \right) \leq 1 - \left\lbrack M_{d}(t) - M_{d}(t - x) \right\rbrack\overline{F}(x),\end{equation*}

and if the $F$ is new worse than used, then

\begin{equation*}\Pr\left( \delta_{t}^{d} \geq x \right) \geq 1 - \left\lbrack M_{d}(t) - M_{d}(t - x) \right\rbrack.\end{equation*}

One can use well-known bounds for the difference $M_{d}(t) - M_{d}(t - x)$ (see, e.g., Chadjiconstantinidis [4]) to obtain bounds for ${\overline{W}}_{t}^{d}(x,y)$ using Proposition 4, and bounds for $\Pr\left( \delta_{t}^{d} \geq x \right)$ using Corollary 4. For example, if the distribution function $F$ is decreasing failure rate, Chadjiconstantinidis [5] proved that

\begin{equation*}G(t) + \frac{\mu_{G}F(t)G_{e}(t)}{\mu F_{e}(t)} \leq M_{d}(t) \leq \frac{G(t)}{\overline{F}(t)},\end{equation*}

from which we get that

\begin{equation*}M_{d}(t - x) - M_{d}(t) \geq G(t - x) - \frac{\mu_{G}F(t - x)G_{e}(t - x)}{\mu F_{e}(t - x)} - \frac{G(t)}{\overline{F}(t)},~0 \leq x \leq t.\end{equation*}

If the distribution function $F$ is decreasing failure rate, it is also new better than used and hence from Proposition 4 we get that

\begin{equation*}{\overline{W}}_{t}^{d}(x,y) \geq \overline{G}(t + y) + \overline{F}(y)\left\{G(t) + G(t - x) - \frac{\mu_{G}F(t - x)G_{e}(t - x)}{\mu F_{e}(t - x)} - \frac{G(t)}{\overline{F}(t)} \right\},0 \leq x \leq t.\end{equation*}

Also, from Corollary 4 we obtain that if the distribution function $F$ is decreasing failure rate, then

\begin{equation*}\Pr\left( \delta_{t}^{d} \geq x \right) \geq 1 + G(t - x) - \frac{\mu_{G}F(t - x)G_{e}(t - x)}{\mu F_{e}(t - x)} - \frac{G(t)}{\overline{F}(t)}, 0 \leq x \leq t.\end{equation*}

A two-sided bound for ${\overline{W}}_{t}^{d}(x,y)$ when the distribution function $F$ is decreasing failure rate, is given in the next Proposition. It should be noted that the lower bound in (14) below is different that obtained above.

Let ${\overline{F}}_{t}(y) = \Pr\left( X_{t} \gt y \right)$ denotes the right-tail of the residual lifetime random variable $X_{t} = X - t\left| X \gt t \right.\ $.

Proposition 5. (i) If the distribution function $F$ is decreasing failure rate, then for any $0 \leq x \leq t$ and $y \geq 0$, it holds that

(14)\begin{equation} \overline{G}(t + y) + {\overline{F}}_{x}(y)\left\lbrack \Pr\left( \delta_{t}^{d}\geq x \right) - \overline{G}(t) \right\rbrack \leq {\overline{W}}_{t}^{d}(x,y)\leq \overline{G}(t + y) + {\overline{F}}_{t}(y)\left\lbrack \Pr\left( \delta_{t}^{d} \geq x \right) - \overline{G}(t) \right\rbrack \end{equation}

(ii) If the distribution function $F$ is IFR, then for any $0 \leq x \leq t$ and $y \geq 0$, it holds that

(15)\begin{equation} \overline{G}(t + y) + {\overline{F}}_{t}(y)\left\lbrack \Pr\left( \delta_{t}^{d} \geq x \right) - \overline{G}(t) \right\rbrack \leq {\overline{W}}_{t}^{d}(x,y)\leq \overline{G}(t + y) + {\overline{F}}_{x}(y)\left\lbrack \Pr\left( \delta_{t}^{d} \geq x \right) - \overline{G}(t) \right\rbrack. \end{equation}

Proof. (i) The right-tail of the residual lifetime is given by ${\overline{F}}_{t}(y) = \frac{\overline{F}(t + y)}{\overline{F}(t)}$, and thus the tail $\overline{F}(t + y - s)$ can be written as

\begin{equation*}\overline{F}(t + y - s) = {\overline{F}}_{t - s}(y)\overline{F}(t - s),~~ 0 \leq s \leq t \end{equation*}

and hence from Proposition 1 we get that ${\overline{W}}_{t}^{d}(x,y)$ also satisfies the equation

(16)\begin{equation} {\overline{W}}_{t}^{d}(x,y) = \overline{G}(t + y) + \int_{0}^{t - x}{{\overline{F}}_{t - s}(y)\overline{F}(t - s)dM_{d}(s)}. \end{equation}

For $0 \leq s \leq t - x$ we also have that $x \leq t - s \leq t$, and since the survival function ${\overline{F}}_{t}(y)$ is a non-decreasing function $t \geq 0$ if the distribution function $F$ is decreasing failure rate, it holds that

\begin{equation*}{\overline{F}}_{x}(y) \leq {\overline{F}}_{t - s}(y) \leq {\overline{F}}_{t}(y).\end{equation*}

Therefore, we have that

\begin{align*} \int_{0}^{t - x}{{\overline{F}}_{x}(y)\overline{F}(t - s)dM_{d}(s)} &\leq \int_{0}^{t - x}{{\overline{F}}_{t - s}(y)\overline{F}(t - s)dM_{d}(s)}\\ & \leq \int_{0}^{t - x}{{\overline{F}}_{t}(y)\overline{F}(t - s)dM_{d}(s)}, \end{align*}

and using (8) the above relationship yields

\begin{align*} {\overline{F}}_{x}(y)\left\lbrack \Pr\left( \delta_{t}^{d} \geq x \right) - \overline{G}(t) \right\rbrack &\leq \int_{0}^{t - x}{{\overline{F}}_{t - s}(y)\overline{F}(t - s)dM_{d}(s)}\\ &\leq {\overline{F}}_{t}(y)\left\lbrack \Pr\left( \delta_{t}^{d} \geq x \right) - \overline{G}(t) \right\rbrack \end{align*}

Now, the two-sided bound in (14) follows immediately from the last relationship and (16).

(ii) The proof of (15) is similar to that in (i) by reversing the inequalities.

By letting $x = 0$ in (14) and (15) we immediately obtain the following two-sided bounds for the right-tail probability $\Pr(\gamma_{t}^{d} \gt y)$.

Corollary 5. If the distribution function $F$ is decreasing failure rate (IFR), then for any $y \geq 0$, it holds that

\begin{equation*}\overline{G}(t + y) + \overline{F}(y)G(t) \leq ( \geq )\Pr(\gamma_{t}^{d} \gt y) \leq ( \geq )\overline{G}(t + y) + {\overline{F}}_{t}(y)G(t).\end{equation*}

The bounds in Proposition 5 and Corollary 5 are exact for $x = 0$ and $y = 0$ respectively, implying that for small values of $x$ and $y$, these bounds are good approximations for ${\overline{W}}_{t}^{d}(x,y)$ and ${\Pr(\gamma}_{t}^{d} \gt y)$.

Another two-sided bound for ${\overline{W}}_{t}^{d}(x,y)$ when the distribution function $F$ is IFR is given in Corollary 15 below.

Theorem 2. If $A(y) = 1 - \overline{A}(y)$ is a distribution function on $(0,\infty)$ satisfying

(17)\begin{equation} {\overline{F}}_{t}(y) \leq \overline{A}(y),~~ t \geq 0, y \geq 0 \end{equation}

then for any $0 \leq x \leq t$ and $y \geq 0$

\begin{equation*}{\overline{W}}_{t}^{d}(x,y) \leq \left\{\frac{\overline{G}(t + y)}{\overline{G}(t)} + \overline{A}(y) \right\} \Pr(\delta_{t}^{d} \geq x).\end{equation*}

Proof. Using that for $0 \leq s \leq t - x \leq t$, from (17) it follows that ${\overline{F}}_{t - s}(y) \leq \overline{A}(y)$. Therefore, from (16) and (8) and we get

\begin{align*} \Pr(\gamma_{t}^{d} \gt y/\delta_{t}^{d} \geq x)& = \ \frac{{\overline{W}}_{t}^{d}(x,y)}{\Pr(\delta_{t}^{d} \geq x)} = \frac{\overline{G}(t + y) + \int_{0}^{t - x}{{\overline{F}}_{t - s}(y)\overline{F}(t - s)dM_{d}(s)}}{\overline{G}(t) + \int_{0}^{t - x}{\overline{F}(t - s)dM_{d}(s)}}\\ & \leq \frac{\overline{G}(t + y) + \overline{A}(y)\int_{0}^{t - x}{\overline{F}(t - s)dM_{d}(s)}}{\overline{G}(t) + \int_{0}^{t - x}{\overline{F}(t - s)dM_{d}(s)}}\\ & \leq \frac{\overline{G}(t + y)}{\overline{G}(t)} + \frac{\overline{A}(y)\int_{0}^{t - x}{\overline{F}(t - s)dM_{d}(s)}}{\int_{0}^{t - x}{\overline{F}(t - s)dM_{d}(s)}}\\ &= \frac{\overline{G}(t + y)}{\overline{G}(t)} + \overline{A}(y), \end{align*}

and hence the result follows.

In the following, we give some applications of Theorem 2.

Corollary 6. If the distribution function $F$ is IFR, then for any $0 \leq x \leq t$ and $y \geq 0$

\begin{equation*}{\overline{W}}_{t}^{d}(x,y) \leq \left\{\frac{\overline{G}(t + y)}{\overline{G}(t)} + e^{- \lambda(0)y} \right\} \Pr(\delta_{t}^{d} \geq x).\end{equation*}

Proof. Under the assumption of IFR inter-arrival times, it holds that $\lambda(t) \geq \lambda(0)$, $t \geq 0$ and hence

\begin{equation*}{\overline{F}}_{t}(y) = \frac{\overline{F}(t + y)}{\overline{F}(t)} = e^{- \int_{t}^{t + y}{\lambda(s)ds}}\leq e^{- \int_{t}^{t + y}{\lambda(0)ds}} = e^{- \lambda(0)y}.\end{equation*}

Thus, Theorem 2 holds with $\overline{A}(y) = e^{- \lambda(0)y}$.

In Corollary 3, we derived an upper bound for the joint right-tail 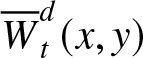${\overline{W}}_{t}^{d}(x,y)$ under the assumption that the distribution function $F$ is new better than used. Using Theorem 2, under the same assumption, we give another different upper bound.

Corollary 7. If the distribution function $F$ is new better than used, then for any $0 \leq x \leq t$ and $y \geq 0$

\begin{equation*}{\overline{W}}_{t}^{d}(x,y) \leq \left\{\frac{\overline{G}(t + y)}{\overline{G}(t)} + \overline{F}(y) \right\} \Pr(\delta_{t}^{d} \geq x).\end{equation*}

Proof. If the distribution function $F$ is new better than used, then

\begin{equation*}{\overline{F}}_{t}(y) = \frac{\overline{F}(t + y)}{\overline{F}(t)} \leq \frac{\overline{F}(t)\overline{F}(y)}{\overline{F}(t)} = \overline{F}(y),\end{equation*}

and thus Theorem 2 holds with $\overline{A}(y) = \overline{F}(y)$.

By letting $x = 0$ in Corollaries 5 and 6, we immediately obtain the following

Corollary 8. (i) If the distribution function $F$ is IFR, then for any $y \geq 0$

\begin{equation*}\Pr(\gamma_{t}^{d} \gt y) \leq \frac{\overline{G}(t + y)}{\overline{G}(t)} + e^{- \lambda(0)y}.\end{equation*}

(ii) If the distribution function $F$ is new better than used, then for any $y \geq 0$

\begin{equation*}\Pr(\gamma_{t}^{d} \gt y) \leq \frac{\overline{G}(t + y)}{\overline{G}(t)} + \overline{F}(y).\end{equation*}

Now, in the following proposition, we shall give some other simple but useful representations for ${\overline{W}}_{t}^{d}(x,y)$.

Proposition 6. For any $0 \leq x \leq t$ and $y \geq 0$, the joint right-tail ${\overline{W}}_{t}^{d}(x,y)$ admits the following representations

(18)\begin{equation} {\overline{W}}_{t}^{d}(x,y) = 1 - \int_{t - x}^{t + y}{\overline{F}(t + y - s)}dM_{d}(s), \end{equation}

(19)\begin{equation} {\overline{W}}_{t}^{d}(x,y) = {\overline{F}}_{e}(x + y) - \int_{0}^{x + y}\overline{F}(s)h_{d}(t + y - s)ds, \end{equation}

and

\begin{align*} {\overline{W}}_{t}^{d}(x,y) = \overline{G}(t + y) + \mu\left\lbrack {\overline{F}}_{e}(x + y)m_{d}(t - x) - {\overline{F}}_{e}(t + y)g(0) \right\rbrack \end{align*}

(20)\begin{equation} - \mu\int_{0}^{t - x}{{\overline{F}}_{e}(t + y - s)dm_{d}(s)}.~~~~~~~~~~~~~~~~ \end{equation}

where $h_{d}(t) = m_{d}(t) - \frac{1}{\mu}$.

Proof. Integrating by parts yields

\begin{align*} \int_{0}^{x + y}{M_{d}(t + y - s)dF(s)} &= - \int_{0}^{x + y}{M_{d}(t + y - s){\overline{F}}^{'}(s)ds}\\ &= - M_{d}(t - x)\overline{F}(x + y) + M_{d}(t + y)\\ &- \int_{0}^{x + y}{m_{d}(t + y - s)}\overline{F}(s)ds\\ &= M_{d}(t + y) - M_{d}(t - x)\overline{F}(x + y)\\ &- \int_{t - x}^{t + y}{\overline{F}(t + y - s)}dM_{d}(s), \end{align*}

and now the result in (18) follows immediately from (2).

Also, (18) can be rewritten as

\begin{align*} {\overline{W}}_{t}^{d}(x,y) &= 1 - \int_{0}^{x + y}{\overline{F}(s)}m_{d}(t + y - s)ds\\ & = 1 - \int_{0}^{x + y}{\overline{F}(s)}\left\{h_{d}(t + y - s) + \frac{1}{\mu} \right\} ds\\ & = 1 - \int_{0}^{x + y}{\overline{F}(s)}\left\{h_{d}(t + y - s) + \frac{1}{\mu} \right\} ds\\ & = 1 - F_{e}(x + y) - \int_{0}^{x + y}\overline{F}(s)h_{d}(t + y - s)ds, \end{align*}

which yields (19).

Finally, from (3), we obtain

\begin{align*} {\overline{W}}_{t}^{d}(x,y) &= \overline{G}(t + y) + \mu\int_{0}^{t - x}{F_{e}(t + y - s)m_{d}(s)ds}\\ & = \overline{G}(t + y) + \mu\left\lbrack {\overline{F}}_{e}(x + y)m_{d}(t - x) - {\overline{F}}_{e}(t + y)m_{d}(0) \right\rbrack\\ & - \mu\int_{0}^{t - x}{{\overline{F}}_{e}(t + y - s)m_{d}^{'}(s)}, \end{align*}

and using that $m_{d}(0) = g(0)$, we get the result in (20).

For $x = t$, from (20), we obtain ${\overline{W}}_{t}^{d}(t,y) = \overline{G}(t + y)$ as we expected, since either side of this relation is equal to the probability that no renewal occurs in the interval $\lbrack 0,\ t + y\rbrack$.

In Proposition 4, we derived a lower bound for 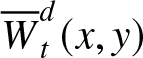${\overline{W}}_{t}^{d}(x,y)$ provided that $F$ is new worse than used. An upper bound for ${\overline{W}}_{t}^{d}(x,y)$ under the same aging property for the distribution function $F$, which is also a refinement of the general upper bound obtained in Theorem 1, is given in the next corollary.

Corollary 9. For any $0 \leq x \leq t$ and $y \geq 0$, if the distribution function $F$is new worse than used, then it holds

(21)\begin{equation} {\overline{W}}_{t}^{d}(x,y) \leq 1 - \overline{F}(y)\overline{F}(x)\left\lbrack M_{d}(t + y) - M_{d}(t - x) \right\rbrack. \end{equation}

The bound in (21) is an improvement of the upper bound given in (3).

Proof. For $s \leq t$, it holds

\begin{equation*}\int_{t - x}^{t + y}{\overline{F}(t + y - s)}dM_{d}(s) \geq \overline{F}(y)\int_{t - x}^{t + y}{\overline{F}(t - s)dM_{d}(s)},\end{equation*}

and since for $t - x \leq s$ we have $t - s \leq x$ implying that $\overline{F}(t - s) \geq \overline{F}(x)$, we get

\begin{align*} \int_{t - x}^{t + y}{\overline{F}(t + y - s)}dM_{d}(s) &\geq \overline{F}(y)\overline{F}(x)\int_{t - x}^{t + y}{dM_{d}(s)}\\ & = \overline{F}(y)\overline{F}(x)\left\lbrack M_{d}(t + y) - M_{d}(t - x) \right\rbrack. \end{align*}

Now, the result follows immediately from (18). Since $\overline{F}(x + y) \geq \overline{F}(y)\overline{F}(x)$, the bound in (21) is tighter than the upper bound given in (3).

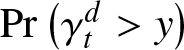It should be noted that the bound in (21) is exact for $x = 0$ and $y = 0$, implying that this upper bound is a good approximation for small values of $x$ and $y$. By letting $x = 0$ and $y = 0$ in Corollary 9, we reveal the upper bounds for $\Pr\left( \gamma_{t}^{d} \gt y \right)$ and $\Pr\left( \delta_{t}^{d} \geq x \right)$ respectively which are given in Corollary 2.

In the following corollary, we give an upper bound for ${\overline{W}}_{t}^{d}(x,y)$ by assuming that the distribution function $F$ belongs to the class of NBUE distributions.

Corollary 10. For any $0 \leq x \leq t$ and $y \geq 0$, if the distribution function $F$is NBUE, then it holds

\begin{equation*}{\overline{W}}_{t}^{d}(x,y) \leq 1 - {\overline{F}}_{e}(x + y)\left\lbrack M_{d}(t + y) - M_{d}(t - x) \right\rbrack.\end{equation*}

Proof. It holds

\begin{align*} \int_{t - x}^{t + y}{\overline{F}(t + y - s)}dM_{d}(s) &\geq \int_{t - x}^{t + y}{{\overline{F}}_{e}(t + y - s)}dM_{d}(s)\\ & \geq \int_{t - x}^{t + y}{{\overline{F}}_{e}(x + y)}dM_{d}(s)\\ & = {\overline{F}}_{e}(x + y)\left\lbrack M_{d}(t + y) - M_{d}(t - x) \right\rbrack, \end{align*}

and thus, the result follows from (18).

The following result is directly obtained from Corollary 10.

Corollary 11. If the distribution function $F$is NBUE, then

\begin{equation*}\Pr{\left( \gamma_{t}^{d} \gt y \right) \leq 1 - {\overline{F}}_{e}(y)\left\lbrack M_{d}(t + y) - M_{d}(t) \right\rbrack},~ y \geq 0\end{equation*}

and

\begin{equation*}\Pr{\left( \delta_{t}^{d} \geq x \right) \leq 1 - {\overline{F}}_{e}(x)\left\lbrack M_{d}(t) - M_{d}(t - x) \right\rbrack}, ~0 \leq x \leq t.\end{equation*}

The upper bounds in Corollaries 10 and 11 are exact for $x = 0$ and $y = 0$, implying that for small values of $x$ and $y$, these bounds are good approximations for ${\overline{W}}_{t}^{d}(x,y)$, ${\Pr(\gamma}_{t}^{d} \gt y)$ and $\Pr(\delta_{t}^{d} \geq x)$.

3.2. Right-tail bounds for recurrence times based on the delayed renewal density

So far, we obtained bounds for 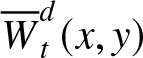${\overline{W}}_{t}^{d}(x,y)$, which are based on $M_{d}(t)$ and/or on $\Pr\left( \delta_{t}^{d} \geq x \right)$. In the sequel, we shall give some bounds for the joint right-tail ${\overline{W}}_{t}^{d}(x,y)$ which are based on the delayed renewal density $m_{d}(t)$ and its monotonicity properties. Hence, using available bounds for $m_{d}(t)$ we can obtain bounds for ${\overline{W}}_{t}^{d}(x,y)$ through the results given in this subsection. Several bounds for the function $m_{d}(t)$ are obtained by Chadjiconstantinidis [4]. Sufficient conditions for $m_{d}(t)$ to be a decreasing (increasing) function can be found in Dermitzakis and Politis [8]. Indeed, from their Propositions 3.1 and 3.2, it follows that if the distribution function $F$ is $DFR$ and the function $\frac{g(t)}{\overline{F}(t)}$ is a strictly increasing (decreasing) function, then $m_{d}(t)$ is an increasing (decreasing) function.

Proposition 7. If the delayed renewal density $m_{d}(t)$ is an increasing (decreasing) function, then for any $0 \leq x \leq t$ and $y \geq 0$ it holds that

(22)\begin{equation} 1 - {\mu F}_{e}(x + y)m_{d}(t + y) \leq ( \geq ){\overline{W}}_{t}^{d}(x,y) \leq ( \geq )1 - {\mu F}_{e}(x + y)m_{d}(t - x). \end{equation}

Proof. Since $m_{d}(t)$ is an increasing (decreasing) function, the same is also true for the function $h_{d}(t) = m_{d}(t) - \frac{1}{\mu}$. Hence, if $0 \leq s \leq x + y$, then $t - x \leq t + y - s \leq t + y$ implying that

\begin{equation*}h_{d}(t - x) \leq ( \geq )h_{d}(t + y - s) \leq ( \geq )h_{d}(t + y).\end{equation*}

Therefore, we have that

\begin{equation*}h_{d}(t - x)\int_{0}^{x + y}\overline{F}(s)ds \leq ( \geq )\int_{0}^{x + y}\overline{F}(s)h_{d}(t + y - s)ds \leq ( \geq )h_{d}(t + y)\int_{0}^{x + y}\overline{F}(s)ds\end{equation*}

or equivalently

\begin{equation*}{\mu F}_{e}(x + y)h_{d}(t - x) \leq ( \geq )\int_{0}^{x + y}\overline{F}(s)h_{d}(t + y - s)ds \leq ( \geq ){\mu F}_{e}(x + y)h_{d}(t + y).\end{equation*}

Now the result follows immediately from the definition of the function $h_{d}(t)$ and the relationship (19).

Using Proposition 7 and by letting $x = 0$ and $y = 0$, we directly obtain the following

Corollary 12. If the delayed renewal density $m_{d}(t)$ is an increasing (decreasing) function, then

\begin{equation*}1 - {\mu F}_{e}(y)m_{d}(t + y) \leq ( \geq ){\Pr(\gamma}_{t}^{d} \gt y) \leq ( \geq )1 - {\mu F}_{e}(y)m_{d}(t), ~y \geq 0\end{equation*}

and

\begin{equation*}1 - {\mu F}_{e}(x)m_{d}(t) \leq ( \geq )\Pr(\delta_{t}^{d} \geq x) \leq ( \geq )1 - {\mu F}_{e}(x)m_{d}(t - x),~0 \leq x \leq t.\end{equation*}

In the following lemma, we give a useful result regarding the asymptotic behavior of the delayed renewal density.

Lemma 1. If the distribution function $F$ is non-lattice, $\mu \lt \infty$, then it holds

\begin{equation*}\lim_{t \rightarrow \infty}{m_{d}(t) = \frac{1}{\mu}}.\end{equation*}

Proof. Consider a function $Z(t)$ satisfying the renewal-type equation

\begin{equation*}Z(t) = r(t) + \int_{0}^{t}{Z(t - z)dF(z)}.\end{equation*}

with $r(t) = g(t) - f_{e}(t)$. Taking Laplace–Stieltjes transforms, we get

\begin{equation*}\widehat{Z}(s) = \widehat{r}(s) + \widehat{Z}(s)\widehat{f}(s)\end{equation*}

or

\begin{equation*}\widehat{Z}(s) = \frac{\widehat{r}(s)}{1 - \widehat{f}(s)} = \frac{\widehat{g}(s)}{1 - \widehat{f}(s)} - \frac{{\widehat{f}}_{e}(s)}{1 - \widehat{f}(s)}.\end{equation*}

Since

\begin{equation*}m_{d}(t) = g(t) + \int_{0}^{t}{m_{d}(t - s)dF(s)},\end{equation*}

we get that

\begin{equation*}{\widehat{m}}_{d}(s) = \frac{\widehat{g}(s)}{1 - \widehat{f}(s)},\end{equation*}

and also, since

\begin{equation*}{\widehat{f}}_{e}(s) = \frac{1}{\mu}\widehat{\overline{F}}(s) = \frac{1 - \widehat{f}(s)}{\mu s},\end{equation*}

it follows that

\begin{equation*}\widehat{Z}(s) = {\widehat{m}}_{d}(s) - \frac{1}{\mu s}.\end{equation*}

Inverting both sides of the last relationship yields

\begin{equation*}Z(t) = m_{d}(t) - \frac{1}{\mu}.\end{equation*}

Therefore, the function $Z(t) = m_{d}(t) - \frac{1}{\mu}$ satisfies the renewal equation

\begin{equation*}Z(t) = g(t) - f_{e}(t) + \int_{0}^{t}{Z(t - z)dF(z)}.\end{equation*}

By applying the Key Renewal Theorem to $Z(t)$, we get

\begin{equation*}\lim_{t \rightarrow \infty}{Z(t) = \frac{1}{\mu}\int_{0}^{\infty}{\left\lbrack g(s) - f_{e}(s)) \right\rbrack ds}},\end{equation*}

that is, it holds $\lim_{t \rightarrow \infty}{Z(t) = 0}$, and hence the result follows.

Remark 1. (i) From (1) and the delayed key renewal theorem we get that the steady state joint complementary distribution function of the backward and forward recurrence times is

\begin{equation*}\lim_{t \rightarrow \infty}{{\overline{W}}_{t}^{d}(x,y)} = \frac{1}{\mu}\int_{x + y}^{\infty}{\overline{F}(t)dt = {\overline{F}}_{e}(x + y)}.\end{equation*}

By taking the limits on both sides of (22), we get

\begin{align*} 1 - {\mu F}_{e}(x + y)\lim_{t \rightarrow \infty}{m_{d}(t + y)} &\leq ( \geq )\lim_{t \rightarrow \infty}{{\overline{W}}_{t}^{d}(x,y)}\\ &\leq ( \geq )1 - {\mu F}_{e}(x + y)\lim_{t \rightarrow \infty}{m_{d}(t - x)}, \end{align*}

and in view of Lemma 1 it follows that

\begin{equation*}1 - {\mu F}_{e}(x + y)\frac{1}{\mu} \leq ( \geq )\lim_{t \rightarrow \infty}{{\overline{W}}_{t}^{d}(x,y)} \leq ( \geq )1 - {\mu F}_{e}(x + y)\frac{1}{\mu},\end{equation*}

which shows that both bounds of Proposition 7 are asymptotically exact, as $t \rightarrow \infty$, provided that the delayed renewal density $m_{d}(t)$ is an increasing (decreasing) function.

(ii) Both bounds in (22) are exact for $x = 0$ and $y = 0$. Therefore, both the bounds in (22) are good approximations for large values of $t$ as well as for small values of $x$ and $y$.

(iii) Similar conclusions also hold for all the bounds of Corollary 12.

Chadjiconstantinidis [4] proved that if the delayed renewal density $m_{d}(t)$ is a non-decreasing (non-increasing) function in $t \geq 0$, then

(23)\begin{equation} m_{d}(t) \leq ( \geq )\frac{g(t)}{\overline{F}(t)},~t \geq 0. \end{equation}

Therefore, from Proposition 7 and Corollary 12, we get weaker but simpler bounds given in the following

Corollary 13. If the delayed renewal density $m_{d}(t)$ is an increasing (decreasing) function, then

\begin{equation*}{\overline{W}}_{t}^{d}(x,y) \geq ( \leq )1 - {\mu F}_{e}(x + y)\frac{g(t + y)}{\overline{F}(t + y)},~0 \leq x \leq t,~y \geq 0,\end{equation*}

\begin{equation*}{\Pr(\gamma}_{t}^{d} \gt y) \geq ( \leq )1 - {\mu F}_{e}(y)\frac{g(t + y)}{\overline{F}(t + y)},~y \geq 0\end{equation*}

and

\begin{equation*}\Pr(\delta_{t}^{d} \geq x) \geq ( \leq )1 - {\mu F}_{e}(x)\frac{g(t)}{\overline{F}(t)},~0 \leq x \leq t.\end{equation*}

Proposition 8. If the delayed renewal density $m_{d}(t)$ is an increasing (decreasing) function, then for any $0 \leq x \leq t$ and $y \geq 0$ it holds

(24)\begin{equation} {\overline{W}}_{t}^{d}(x,y) \leq ( \geq )\overline{G}(t + y) + {\mu m}_{d}(t - x)\left\lbrack F_{e}(t + y) - F_{e}(x + y) \right\rbrack, \end{equation}

and

(25)\begin{equation} {\overline{W}}_{t}^{d}(x,y) \geq ( \leq )\overline{G}(t + y) + \frac{\mu}{t - x}\left\lbrack F_{e}(t + y) - F_{e}(x + y) \right\rbrack M_{d}(t - x). \end{equation}

Proof. Since $m_{d}(t)$ is an increasing (decreasing) function, from (1), we get

\begin{align*} {\overline{W}}_{t}^{d}(x,y) &= \overline{G}(t + y) + \int_{0}^{t - x}{\overline{F}(t + y - s)m_{d}(s)ds}\\ &\leq ( \geq )\overline{G}(t + y) + m_{d}(t - x)\int_{0}^{t - x}{\overline{F}(t + y - s)ds}\\ &= \overline{G}(t + y) + m_{d}(t - x)\int_{x + y}^{t + y}\overline{F}(s)ds\\ &= \overline{G}(t + y) + \mu m_{d}(t - x)\left\lbrack F_{e}(t + y) - F_{e}(x + y) \right\rbrack, \end{align*}

and the result in (24) follows from (1) and the last relationship.

If $m_{d}(t)$ is an increasing (decreasing) function, then

\begin{equation*}\left( \frac{d}{ds}m_{d}(s) \right)\left( \frac{d}{ds}\overline{F}(t + y - s) \right) \geq ( \leq )0,\end{equation*}

and hence from Lemma 3 of Cai and Garrido [3] it follows that

\begin{align*} \int_{0}^{t - x}\overline{F}(t + y - s)m_{d}(s)ds &\geq ( \leq )\frac{1}{t - x}\int_{0}^{t - x}{\overline{F}(t + y - s)ds\int_{0}^{t - x}{m_{d}(s)ds}} \\ &= \frac{1}{t - x}\left( \int_{x + y}^{t + y}\overline{F}(s)ds \right)M_{d}(t - x). \end{align*}

Now, the result in (25) follows directly from (1) and the last relationship.

Remark 2. (i) By taking the limits on the RHS of (24) we get

\begin{align*} \lim_{t \rightarrow \infty}\left\{\overline{G}(t + y) + {\mu m}_{d}(t - x)\left\lbrack F_{e}(t + y) - F_{e}(x + y) \right\rbrack \right\} &= \mu\lim_{t \rightarrow \infty}{m(t - x)}\left\lbrack 1 - F_{e}(x + y) \right\rbrack\\ &= {\overline{F}}_{e}(x + y), \end{align*}

where the last equality follows from Lemma 1. This shows that the bound in (24) is asymptotically exact as $t \rightarrow \infty$.

(ii) Similarly, by taking the limits on the RHS of (25), we get

\begin{align*} \lim_{t \rightarrow \infty}\left\{\overline{G}(t + y) + \frac{\mu}{t - x}\left\lbrack F_{e}(t + y) - F_{e}(x + y) \right\rbrack M_{d}(t - x) \right\}=\\= \left\lbrack 1 - F_{e}(x + y) \right\rbrack\lim_{t \rightarrow \infty}\frac{\mu}{t - x}M_{d}(t - x)= {\overline{F}}_{e}(x + y), \end{align*}

since from the elementary renewal theorem, it is well known that $M_{d}(t)$ also converges to $\frac{t}{\mu}$ as $t \rightarrow \infty$ (see, e.g., in Th. 7.12 of Beichelt [2]. Therefore, the bound in (25) is asymptotically exact as $t \rightarrow \infty$.

Using (24) and (25), we get the following weaker but simpler bounds under the assumption that the delayed renewal function $m_{d}(t)$ is an increasing (decreasing) function

\begin{equation*}{\overline{W}}_{t}^{d}(x,y) \leq ( \geq )\overline{G}(t + y) + \mu\frac{g(t - x)}{\overline{F}(t - x)}\left\lbrack F_{e}(t + y) - F_{e}(x + y) \right\rbrack,~0 \leq x \leq t,~y \geq 0.\end{equation*}

Corollary 14. If the delayed renewal density $m_{d}(t)$ is an increasing (decreasing) function, then for $0 \leq x \leq t$ and $y \geq 0$ it holds

\begin{equation*}{\overline{W}}_{t}^{d}(x,y) \leq ( \geq )\overline{G}(x + y).\end{equation*}

Proof. Chadjiconstantinidis [4] proved that 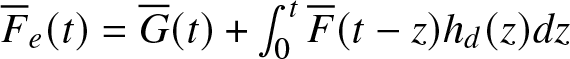${\overline{F}}_{e}(t) = \overline{G}(t) + \int_{0}^{t}{\overline{F}(t - z)h_{d}(z)dz\ }$and hence

\begin{align*} {\overline{F}}_{e}(x + y)& = \overline{G}(x + y) + \int_{0}^{x + y}{\overline{F}(x + y - z)h_{d}(z)dz\ }\\ &= \ \overline{G}(x + y) + \int_{0}^{x + y}{\overline{F}(z)h_{d}(x + y - z)dz\ }. \end{align*}

Since $m_{d}(t)$ is an increasing (decreasing) function, the same is also true for the function 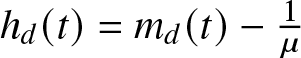$h_{d}(t) = m_{d}(t) - \frac{1}{\mu}$. Therefore, using the above and (19) we get for $x \leq t$

\begin{align*} {\overline{F}}_{e}(x + y) &\leq ( \geq )\overline{G}(x + y) + \int_{0}^{x + y}{\overline{F}(z)h_{d}(t + y - z)dz\ }\\ &= \overline{G}(x + y) + {\overline{F}}_{e}(x + y) - {\overline{W}}_{t}^{d}(x,y), \end{align*}

which gives the required result.

Proposition 9. If the delayed renewal density $m_{d}(t)$ is an increasing (decreasing) function, then for any $0 \leq x \leq t$ it holds

\begin{equation*}\Pr{\left( \gamma_{t}^{d} \gt x \right) \leq ( \geq )\ \Pr(\delta_{t}^{d} \geq x).}\end{equation*}

Proof. Since $m_{d}(t)$ is an increasing (decreasing) function, the same is also true for the function $h_{d}(t) = m_{d}(t) - \frac{1}{\mu}$. Hence, if $0 \leq s \leq t$ and $x \geq 0$ we have

\begin{equation*}h_{d}(t - z) \leq ( \geq )h_{d}(t + x - s).\end{equation*}

Therefore, we get that

\begin{equation*}{\overline{F}}_{e}(x) - \int_{0}^{x + y}\overline{F}(s)h_{d}(t - s)ds \geq ( \leq ){\overline{F}}_{e}(x) - \int_{0}^{x + y}\overline{F}(s)h_{d}(t + x - s)ds.\end{equation*}

By letting $y = 0$, it follows that

\begin{equation*}{\overline{F}}_{e}(x) - \int_{0}^{x}\overline{F}(s)h_{d}(t - s)ds \geq ( \leq ){\overline{F}}_{e}(x) - \int_{0}^{x}\overline{F}(s)h_{d}(t + x - s)ds,\end{equation*}

and hence from (19) the proof is completed.

Now, let us define for $0 \leq x \leq t$ and $y \geq 0$, the functions $\phi_{d,1}(x,y,t)$ and $\phi_{d,2}(x,y,t)$,

\begin{equation*}\phi_{d,1}(x,y,t)\ = \int_{0}^{x + y}{\ \overline{F}(z)h_{d,1}(t + y - z)dz},\end{equation*}

\begin{equation*}\phi_{d,2}(x,y,t)\ = \int_{0}^{x + y}{\ \overline{F}(z)h_{d,2}(t + y - z)dz},\end{equation*}

where

\begin{equation*}h_{d,1}(t) = g(t) - \frac{\overline{F}(t)}{\mu} + \lambda(0)\left( {\overline{F}}_{e}(t) - \overline{G}(t) \right),\end{equation*}

\begin{equation*}h_{d,2}(t) = g(t) - \frac{\overline{F}(t)}{\mu} + \lambda(t)\left( {\overline{F}}_{e}(t) - \overline{G}(t) \right).\end{equation*}

In the following result, we give a two-sided bound for the ${\overline{W}}_{t}^{d}(x,y)$ under the assumption that the distribution function F is decreasing failure rate (IFR).

Corollary 15. If the distribution function F is IFR, then

\begin{equation*}{\overline{F}}_{e}(x + y) - \phi_{d,2}(x,y,t) \geq \ {\overline{W}}_{t}^{d}(x,y)\ \geq \ {\overline{F}}_{e}(x + y) - \phi_{d,1}(x,y,t).\end{equation*}

Proof. Chadjiconstantinidis [4] proved the following two-sided bound for the delayed renewal density $m_{d}(t)$

\begin{equation*}g(t) + \frac{F(t)}{\mu} + \lambda(0)\left( {\overline{F}}_{e}(t) - \overline{G}(t) \right) \leq m_{d}(t) \leq g(t) + \frac{F(t)}{\mu} + \lambda(t)\left( {\overline{F}}_{e}(t) - \overline{G}(t) \right).\end{equation*}

Since $h_{d}(t) = m_{d}(t) - \frac{1}{\mu}$, from the above bounds we get

\begin{equation*}h_{d,1}(t) \leq h_{d}(t) \leq h_{d,2}(t),\end{equation*}

and thus

\begin{equation*}- \phi_{d,2}(x,y,t) \leq - \int_{0}^{x + y}{\overline{F}(s)h_{d}(t + y - s)ds \leq -}\phi_{d,1}(x,y,t)\end{equation*}

and hence the result follows from (19).

In the following result, we give a lower (upper) bound for ${\overline{W}}_{t}^{d}(x,y)$ which is based on the monotonicity of the quantity $\overline{F}(t + y - s)/\overline{G}(t + y)$ with respect to $y$.

Proposition 10. For any $0 \leq y_{1} \leq y_{2}$, if it holds

(26)\begin{equation} \frac{\overline{F}\left( t + y_{1} - s \right)}{\overline{G}\left( t + y_{1} \right)} \geq ( \leq )\frac{\overline{F}\left( t + y_{2} - s \right)}{\overline{G}\left( t + y_{2} \right)}, \end{equation}

then

\begin{equation*}{\overline{W}}_{t}^{d}(x,y) \leq ( \geq )\frac{\overline{G}(t + y)}{\overline{G}(t)}\Pr(\delta_{t}^{d} \geq x),~t \geq 0.\end{equation*}

Proof. Assuming (26) holds, multiplying both sides with $m_{d}(s)$, then integrating with respect to $s$ in $(0,\ t - x)$ and finally adding one in both sides of (26), we get

\begin{equation*}1 + \int_{0}^{t - x}\frac{\overline{F}\left( t + y_{1} - s \right)}{\overline{G}\left( t + y_{1} \right)}m_{d}(s)ds \geq ( \leq )1 + \int_{0}^{t - x}\frac{\overline{F}\left( t + y_{2} - s \right)}{\overline{G}\left( t + y_{2} \right)}m_{d}(s)ds.\end{equation*}

In view of equation (1), the above inequality could be written as

(27)\begin{equation} {\overline{W}}_{t}^{d}\left( x,y_{1} \right)/\overline{G}\left( t + y_{1} \right) \geq ( \leq ){\overline{W}}_{t}^{d}\left( x,y_{2} \right)/\overline{G}\left( t + y_{2} \right), \end{equation}

from which it follows that ${\overline{W}}_{t}^{d}(x,y)/\overline{G}(t + y)$ is a decreasing (increasing) function in $y \geq 0$. By letting $y_{1} = 0$ and $y_{2}\ = y$ into (27) we get

\begin{equation*}\Pr(\delta_{t}^{d} \geq x)/\overline{G}(t) \geq ( \leq ){\overline{W}}_{t}^{d}(x,y)/\overline{G}(t + y),\end{equation*}

and by rearranging the terms, we prove the assertion.

Before we proceed, we need the following lemma (see, e.g., Apostol [1]).

Lemma 2. Let f and g be two integrable functions over a finite interval $\lbrack a,b\rbrack$, which have different monotonicity within that interval. Then, it holds that

\begin{equation*}\int_{a}^{b}{f(x)g(x)dx \leq \ \frac{1}{b - a}}\int_{a}^{b}{f(x)dx\int_{a}^{b}{g(x)dx.}}\end{equation*}

Moreover, if f and g have the same monotonicity on interval $\lbrack a,b\rbrack$, the inequality of the above relation is reserved.

Proposition 11. If the distribution function $F$ is $DFR$ and the function 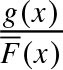$\frac{g(x)}{\overline{F}(x)}$ is a strictly decreasing (increasing) function, then

\begin{equation*}{\overline{W}}_{t}^{d}(x,y) \leq ( \geq )\overline{G}(t + y) + \frac{\mu}{t - x}\left( {\overline{F}}_{e}(x + y) - \ {\overline{F}}_{e}(t + y) \right)M_{d}(t - x).\end{equation*}

Proof. From Propositions 3.1 and 3.2 of Dermitzakis and Politis [8], it follows that if the distribution function $F$ is $DFR$ and the function $\frac{g(x)}{\overline{F}(x)}$ is a strictly decreasing (increasing) function, then $m_{d}(x)$ is a decreasing (increasing) function, implying that the delayed renewal function $M_{d}(t)$ is concave (convex). Then it holds

\begin{equation*}\left( \frac{d}{ds}\overline{F}(t + y - s) \right)\left( \frac{d}{ds}M_{d} \right) \leq ( \geq )0,\end{equation*}

and thus, using Lemma 2, from equation (1), we get

\begin{align*} {\overline{W}}_{t}^{d}(x,y) &= \overline{G}(t + y) + \int_{0}^{t - x}{\overline{F}(t + y - s)dM_{d}(s)}\\ &\leq ( \geq )\overline{G}(t + y) + \frac{1}{t - x}\int_{0}^{t - x}{\overline{F}(t + y - s)d{s\int_{0}^{t - x}{m_{d}(s)}ds}_{\ }}\\ &= \overline{G}(t + y) + \frac{1}{t - x}\int_{x + y}^{t + y}{\overline{F}(s)d{s\int_{0}^{t - x}{m_{d}(s)}ds}_{\ }}\\ &= \overline{G}(t + y) + \frac{\mu}{t - x}\left( {\overline{F}}_{e}(x + y) - \ {\overline{F}}_{e}(t + y) \right)M_{d}(t - x). \end{align*}

In the following result, we give another formula for the joint right-tail probability 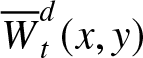${\overline{W}}_{t}^{d}(x,y)$ of the backward and forward recurrence time in a delayed renewal process, in terms of the right-tail ${\overline{W}}_{t}^{\ }(x,y)$ of the backward and forward recurrence time in an ordinary renewal process. The recurrence times in an ordinary renewal process have been studied extensively, and results related to the joint survival function of the backward and forward recurrence times ${\overline{W}}_{t}^{\ }(x,y)$ are available; see, for example, Losidis et al. [17] and Chadjiconstantinidis and Politis [6]. Let $m(t)$ denote the renewal density in an ordinary renewal process.

Proposition 12. For any $0 \leq x \leq t$, and $y \geq 0$ it holds that

\begin{equation*}{\overline{W}}_{t}^{d}(x,y)\ = {\overline{W}}_{t}^{\ }(x,y) + \int_{0}^{x + y}{\overline{F}(z)}\left( m(t + y - z) - m_{d}(t + y - z) \right)\ dz.\end{equation*}

Proof. Let the function $h(t)\ = \ m(t) - \frac{1}{\mu}$. Since the quantity $h_{d}(t)$ can also be written as $h_{d}(t) = m_{d}(t) + h(t)\ - \ m(t)$, then (19) yields

\begin{align*} {\overline{W}}_{t}^{d}(x,y) &= {\overline{F}}_{e}(x + y) - \int_{0}^{x + y}\overline{F}(s)h(t + y - s)ds\\ &+ \int_{0}^{x + y}\overline{F}(s)\left( m(t + y - s) - m_{d}(t + y - s) \right)ds, \end{align*}

and using that (see, e.g., Losidis et al. [17] and Chadjiconstantinidis and Politis [6])

\begin{equation*}{\overline{W}}_{t}^{\ }(x,y)\ = {\overline{F}}_{e}(x + y) - \int_{0}^{x + y}\overline{F}(s)h(t + y - s)ds,\end{equation*}

the result follows the last two relationships.

Remark 3. The delayed or modified renewal process differs from an ordinary renewal process in that the distribution of $X_{1}$ is different from that of the subsequent $X_{i}$, $i \geq 2$. In an ordinary renewal process, we have $G = F$, which implies $m_d(t) = m(t)$. Then, from Proposition 12, it follows directly that $ {\overline{W}}_{t}^{d}(x,y) = {\overline{W}}_{t}(x,y),$ and in this case, all our results are applicable to the ordinary renewal process.

The following result follows directly from Proposition 12.

Corollary 16. If $m(t) \geq ( \leq )m_{d}(t)$, then

\begin{equation*}{\overline{W}}_{t}^{d}(x,y)\ \geq ( \leq ){\overline{W}}_{t}^{\ }(x,y). \end{equation*}

4. Numerical examples

Here, we give some examples to illustrate numerically the performance of the bounds obtained in Section 3. In some tables, we also report the relative error of the upper bound, computed as $URE = \text{Upper Bound} / \text{Exact Value} - 1$, while in other tables we report the relative error of the lower bound, computed as $LRE = \text{Lower Bound} / \text{Exact Value} - 1$.

Example 1. Assume that F is a mixture of two exponentials with density function $f(t) = \frac{3}{2}e^{- 3t} + \frac{7}{2}e^{- 7t},\ \ t \geq 0.$ We also assume that the distribution function of the first inter-arrival time has density $g(t) = 2te^{- t^{2}}\ ,t \geq 0\ $, that is a Weibull with shape parameter $k = 2$ and a scale parameter $c = 1$.

In Table 1, by setting $x = \ 0.01$ and $y = 0.01$, we illustrate the exact value of the joint right-tail distribution of the forward and backward recurrence time given by Proposition 1, and the upper and lower bounds from Theorem 1.

Table 1. Exact values for ${\overline{W}}_{t}^{d}(x,y)$ and bounds given by Theorem 1.

In Proposition 4, assuming that the distribution F is new worse than used, we offer a lower bound for the joint right tail of the backward and forward recurrence time. Table 2 illustrates the performance of this bound.

Table 2. Exact values for ${\overline{W}}_{t}^{d}(x,y)$ and lower bound from Proposition 4.

Example 2. In this example, we assume that the first inter-arrival time $X_{1}$ follows a Weibull distribution with shape parameter $k=2$ and scale parameter $c=1$, so it has the probability density function $g(t) = 2te^{- t^{2}},\ t \geq 0$. The first moment is $\mu_{1,G} = \sqrt{\pi}/2$, and the right tail is $\overline{G}(t) = e^{- t^{2}}$. We also assume that all other inter-arrival times $X_{i}$ ( $i \geq 2$) follow a Gamma (2,1) distribution with density $f(t) = te^{- t},\ t \geq 0$.

In Table 3, by setting $x = 0.1$ and $y = 0.5$, we illustrate the exact value of the joint right-tail distribution of the forward and backward recurrence times given by Proposition 1, and the upper and lower bounds from Theorem 1.

Table 3. Exact values for ${\overline{W}}_{t}^{d}(x,y)$ and bounds given by Theorem 1.

Employing equation (6), we get:

\begin{equation*} \Pr{\left( \gamma_{t}^{d} \gt y \right) = e^{- (t + y)^{2}} + \frac{1}{2}}e^{- t^{2} - y}\left\{- 2(1 + y) + e^{( - 2 + t)t} \right.\ y + e^{2t}(2 + y) \end{equation*}

\begin{equation*} \left. \ + \left. \ e\sqrt{\pi}yErf\lbrack 1\rbrack \right\rbrack - e^{( - 1 + t)^{2}}\sqrt{\pi}yErf\lbrack 1 - t\rbrack \right\} .\end{equation*}

Using Corollary 5, we can build lower and upper bounds for the right tail of the forward recurrence time, assuming that the distribution function $F$ is IFR. This holds true given that is a Gamma(2,1). In Table 4, we demonstrate the performance of those bounds for $y = 0.1$.

Table 4. Exact values for $\Pr\left( \gamma_{t}^{d} \gt y \right)$ and bounds from Corollary 5, for $y=0.1$.

Example 3. Assume that the first inter-arrival time $X_{1}$ follows a Lindley distribution with parameter $\theta = 1$, so it has probability density 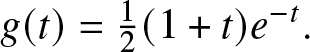$ g(t) = \frac{1}{2}(1 + t)e^{- t}.$ The first moment is equal to $\mu_{1,G} = \frac{3}{2}$, and the right tail is $ \overline{G}(t) = \frac{1}{2}e^{- t}(2 + t).$ We also assume that all the other inter-arrival times $X_{i}, (i \geq 2)$ follow a Gamma ( $2,1$) distribution with density $ f(t) = te^{- t}, \quad t \geq 0.$ In this case, the first moment is equal to $\mu = 2$, and the equilibrium right tail is $ {\overline{F}}_{e}(t) = \frac{1}{2}e^{- t}(2 + t).$ In our example, it holds that $\overline{G}(t) = {\overline{F}}_{e}(t)$, and then it is well known that $ M_{d}(t) = \frac{t}{\mu},$ and $ {\overline{W}}_{t}^{d}(x,y) = {\overline{F}}_{e}(x + y).$ Setting into the latter $x = 0$, we get $ \Pr\left( \delta_{t}^{d} \geq x \right) = {\overline{W}}_{t}^{d}(x,0) = {\overline{F}}_{e}(x).$ Given that the distribution function F is a Gamma (2,1), we can employ Corollary 4 and calculate an upper bound for the quantity 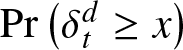$\Pr\left( \delta_{t}^{d} \geq x \right)$, knowing that the distribution $F$ is new better than used. In that case, the upper bound is $ \Pr\left( \delta_{t}^{d} \geq x \right) \leq 1 - \frac{1}{2}e^{- x}x(1 + x).$ Similarly, given that $F$ is NBUE, we could engage Corollary 11, and then an upper bound for the right-tail of the backward recurrence time is 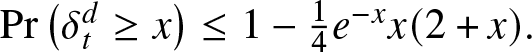$ \Pr\left( \delta_{t}^{d} \geq x \right) \leq 1 - \frac{1}{4}e^{- x}x(2 + x).$ In Table 5, we give for some values of $x$, the exact values, as well as the values of the bounds for $\Pr\left( \delta_{t}^{d} \geq x \right)$ obtained from Corollaries 4 and 11.

Table 5. Exact values for $\Pr\left( \delta_{t}^{d} \geq x \right)$ and bounds from Corollary 4 and Corollary 11.