 $\ell$ LOCAL LANGLANDS CORRESPONDENCE BY NILPOTENT GAMMA FACTORS
$\ell$ LOCAL LANGLANDS CORRESPONDENCE BY NILPOTENT GAMMA FACTORS
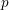 $p$
-adic Langlands program for
$p$
-adic Langlands program for
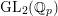 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
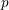 $p$ local-global compatibility for
$p$ local-global compatibility for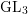 $\text{GL}_{3}$ in the ordinary case
$\text{GL}_{3}$ in the ordinary case