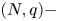 Laplacian equation in $\mathbb {R}^N$
Laplacian equation in $\mathbb {R}^N$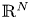 with new exponential growth conditions
with new exponential growth conditions
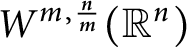 $W^{m,\frac {n}{m}}(\mathbb {R}^n)$
: a simple approach
$W^{m,\frac {n}{m}}(\mathbb {R}^n)$
: a simple approach