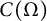 $C(\Omega)$ to a
$C(\Omega)$ to a 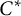 $C^*$-algebra
$C^*$-algebra
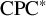 ${\mathrm {CPC}^*}$-Systems
${\mathrm {CPC}^*}$-Systems
 $ \Gamma $ and finite dimensional tracial boundaries
$ \Gamma $ and finite dimensional tracial boundaries
 $^*$-covers of an operator algebra
$^*$-covers of an operator algebra
 $C^*(R_+)\rtimes R^\times $
$C^*(R_+)\rtimes R^\times $
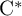 $\mathrm {C}^*$-ALGEBRAS
$\mathrm {C}^*$-ALGEBRAS
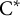 $\mathrm{C}^{*}$-algebras hereditarily containing nonzero, square-zero elements
$\mathrm{C}^{*}$-algebras hereditarily containing nonzero, square-zero elements