We study hyperbolicity properties of the moduli space of polarized abelian varieties (also known as the Siegel modular variety) in characteristic p. Our method uses the plethysm operation for Schur functors as a key ingredient and requires a new positivity notion for vector bundles in characteristic p called 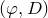$(\varphi,D)$-ampleness. Generalizing what was known for the Hodge line bundle, we also show that many automorphic vector bundles on the Siegel modular variety are 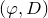$(\varphi,D)$-ample.

For the locally symmetric space X attached to an arithmetic subgroup of an algebraic group G of ℚ-rank r, we construct a compact manifold by gluing together 2r copies of the Borel–Serre compactification of X. We apply the classical Lefschetz fixed point formula to and get formulas for the traces of Hecke operators ℋ acting on the cohomology of X. We allow twistings of ℋ by outer automorphisms η of G. We stabilize this topological trace formula and compare it with the corresponding formula for an endoscopic group of the pair (G,η) . As an application, we deduce a weak lifting theorem for the lifting of automorphic representations from Siegel modular groups to general linear groups.