We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We analyse the asymptotic behaviour of a biological system described by a stochastic competition model with 
$n$ species and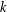 
$k$ resources (chemostat model), in which the species mortality rates are influenced by the fractional Brownian motion of the extrinsic noise environment. By constructing a Lyapunov functional, the persistence and extinction criteria are derived in the mean square sense. Some examples are given to illustrate the effectiveness of the theoretical result.
