Refine search
Actions for selected content:
15 results
2 - Linear Mappings
-
- Book:
- Advanced Linear Algebra
- Published online:
- 27 May 2025
- Print publication:
- 12 June 2025, pp 38-82
-
- Chapter
- Export citation
A Note on the Determination of Configuration and Weights for a Class of Individual Scaling Models
-
- Journal:
- Psychometrika / Volume 50 / Issue 4 / December 1985
- Published online by Cambridge University Press:
- 01 January 2025, pp. 539-542
-
- Article
- Export citation
2 - Network Metrics
- from Part I - A Brief Guide to Network Science
-
- Book:
- Behavioral Network Science
- Published online:
- 08 November 2024
- Print publication:
- 19 December 2024, pp 24-45
-
- Chapter
- Export citation
LEFT AND RIGHT EIGENVECTORS OF A VARIANT OF THE SYLVESTER–KAC MATRIX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 19 June 2023, pp. 316-326
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
9 - Eigenvalues, Eigenvectors, and Geometric Multiplicity
-
- Book:
- Matrix Mathematics
- Published online:
- 29 September 2023
- Print publication:
- 25 May 2023, pp 180-201
-
- Chapter
- Export citation
Magnetic shape fabric analysis from syntectonic granites: a study based on the eigenvalue method
-
- Journal:
- Geological Magazine / Volume 160 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 20 September 2022, pp. 222-234
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
24 - Empirical Orthogonal Function Analysis
-
- Book:
- Time Series Data Analysis in Oceanography
- Published online:
- 21 April 2022
- Print publication:
- 05 May 2022, pp 427-457
-
- Chapter
- Export citation
3 - Coupled Oscillators
-
- Book:
- Mathematical Methods for Oscillations and Waves
- Published online:
- 02 April 2020
- Print publication:
- 05 March 2020, pp 65-89
-
- Chapter
- Export citation
11 - Dimensionality Reduction
-
- Book:
- Mining of Massive Datasets
- Published online:
- 16 April 2020
- Print publication:
- 09 January 2020, pp 410-440
-
- Chapter
- Export citation
7 - Linear Algebra
-
- Book:
- The Student's Introduction to <I>Mathematica</I> and the Wolfram Language
- Published online:
- 01 April 2019
- Print publication:
- 16 May 2019, pp 335-382
-
- Chapter
- Export citation
Yaglom limits can depend on the starting state
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 1-34
- Print publication:
- March 2018
-
- Article
- Export citation
Inequalities for Eigenvalues of a General Clamped Plate Problem
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 1 / 01 March 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 88-97
- Print publication:
- 01 March 2012
-
- Article
-
- You have access
- Export citation
Explicit eigenvalues and inverses of several Toeplitz matrices
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 1 / July 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 73-97
-
- Article
-
- You have access
- Export citation
PERTURBATION RESULTS RELATED TO PALINDROMIC EIGENVALUE PROBLEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 87-100
-
- Article
-
- You have access
- Export citation
EXPLICIT EIGENVALUES AND INVERSES OF TRIDIAGONAL TOEPLITZ MATRICES WITH FOUR PERTURBED CORNERS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 3 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 361-387
-
- Article
-
- You have access
- Export citation
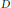
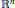
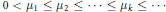
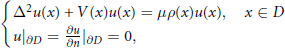
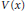
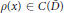
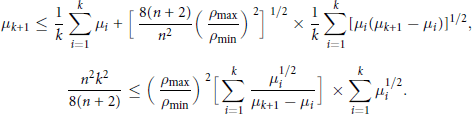
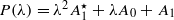 with
with 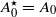 (where
(where 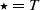 or
or 