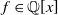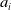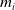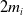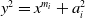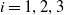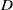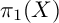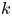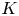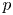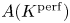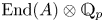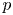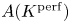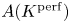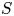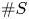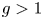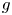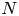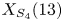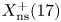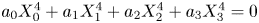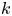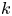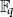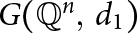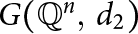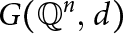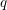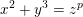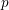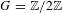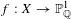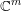Refine search
Actions for selected content:
47 results
Families of twists of tuples of hyperelliptic curves
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 02 February 2026, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the L-polynomials of curves over finite fields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 06 February 2025, pp. 1-49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KOBAYASHI-OCHIAI’S FINITENESS THEOREM FOR ORBIFOLD PAIRS OF GENERAL TYPE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 17 April 2024, pp. 2713-2732
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LOCAL SECTIONS OF ARITHMETIC FUNDAMENTAL GROUPS OF p-ADIC CURVES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 20 December 2023, pp. 462-487
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Perfect points of abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 08 September 2023, pp. 2261-2278
- Print publication:
- November 2023
-
- Article
- Export citation
Weight filtrations on Selmer schemes and the effective Chabauty–Kim method
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 20 June 2023, pp. 1531-1605
- Print publication:
- July 2023
-
- Article
- Export citation
Quadratic Chabauty for modular curves: algorithms and examples
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1111-1152
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Diagonal quartic surfaces with a Brauer–Manin obstruction
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 17 March 2023, pp. 659-710
- Print publication:
- April 2023
-
- Article
- Export citation
On the distribution of rational points on ramified covers of abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 07 December 2022, pp. 2109-2155
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Average-case complexity of the Euclidean algorithm with a fixed polynomial over a finite field
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 166-183
-
- Article
- Export citation
GEOMETRIC QUADRATIC CHABAUTY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 17 June 2021, pp. 279-333
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- Export citation
Rational points and derived equivalence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 1036-1050
- Print publication:
- May 2021
-
- Article
- Export citation
On Single-Distance Graphs on the Rational Points in Euclidean Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 29 July 2020, pp. 13-24
- Print publication:
- March 2021
-
- Article
- Export citation
The size of the primes obstructing the existence of rational points
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 15 May 2020, pp. 652-704
- Print publication:
- April 2021
-
- Article
- Export citation
A Witt Nadel vanishing theorem for threefolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 3 / March 2020
- Published online by Cambridge University Press:
- 13 January 2020, pp. 435-475
- Print publication:
- March 2020
-
- Article
- Export citation
The generalized Fermat equation with exponents 2, 3,
 $n$
$n$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 26 November 2019, pp. 77-113
- Print publication:
- January 2020
-
- Article
- Export citation
DENSITY RESULTS FOR SPECIALIZATION SETS OF GALOIS COVERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 25 October 2019, pp. 1455-1496
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
An effective Chabauty–Kim theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 14 May 2019, pp. 1057-1075
- Print publication:
- June 2019
-
- Article
- Export citation
Corrigendum: Torsion points on abelian varieties of CM-type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 3 / March 2018
- Published online by Cambridge University Press:
- 26 December 2017, p. 594
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation
The Pila–Wilkie theorem for subanalytic families: a complex analytic approach
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 10 / October 2017
- Published online by Cambridge University Press:
- 27 July 2017, pp. 2171-2194
- Print publication:
- October 2017
-
- Article
- Export citation