We determine spatially-bounded rogue waves in the Davey–Stewartson I equation. We show that these rogue waves can be obtained when a single or multiple internal parameters in the higher-order rational solution of the Davey–Stewartson I equation are real and large, and the order-index vector of this higher-order rational solution has even length and comprises pairs of the form 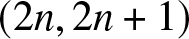$(2n, 2n+1)$, where 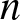$n$ is a positive integer. Under these conditions and another nondegeneracy condition on the root curve of a certain double-real-variable polynomial, the higher-order rational solution will exhibit spatially-bounded rogue waves that arise from a uniform background with some time-varying lumps on it, reach high amplitude in limited space, and then disappear into the same background again. The crests of these rogue waves form a single or multiple closed curves that are generically disconnected from each other on the spatial plane, and are analytically predicted by the root curve mentioned above. We also derive uniformly-valid asymptotic approximations for these spatially-bounded rogue waves in the large-parameter regime. Near the crests of these rogue waves, these asymptotic approximations reduce to simple expressions. Our asymptotic approximations of these rogue waves are compared to true solutions, and good agreement is demonstrated.