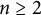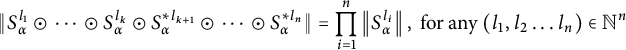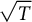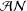Skip to main content Accessibility help
×
  1. Home
  2. Search

Refine search

Refine search

Access:
Content type:
Publication date:
Apply   From and To filters
Subject: Show more
Journals Show more
Publishers: Show more
Societies Show more
Series: Show more
Collections: Show more

Actions for selected content:

Select all | Deselect all
  • View selected items
  • Export citations
  • Download PDF (zip)
  • Save to Kindle
  • Save to Dropbox
  • Save to Google Drive

Save Search

You can save your searches here and later view and run them again in "My saved searches".

Please provide a title, maximum of 40 characters.
Cancel
×

3 results

  • The norms for symmetric and antisymmetric tensor products of the weighted shift operators

  • Part of
  • Xiance Tian, Penghui Wang, Zeyou Zhu
  • Journal:
    Canadian Journal of Mathematics , First View
    Published online by Cambridge University Press:
    26 January 2026, pp. 1-27

  • In the present article, we study the norms for symmetric and antisymmetric tensor products of weighted shift operators. By proving that for 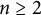$n\geq 2$,

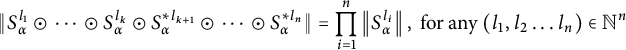    $$ \begin{align*}\|S_{\alpha}^{l_1}\odot\cdots \odot S_{\alpha}^{l_k}\odot S_{\alpha}^{*l_{k+1}}\odot\cdots \odot S_{\alpha}^{*l_{n}}\| =\mathop{\prod}_{i=1}^n\left \| S_{\alpha}^{{l_{i}}}\right\|, \text{ for any} \ (l_1,l_2\ldots l_n)\in\mathbb N^n\end{align*} $$
    if and only if the weight satisfies the regularity condition, we partially solve [see Problems 6 and 7 in Garcia et al. (2025, Canad. J. Math., 77, 324–346)]. It will be seen that most weighted shift operators on function spaces, including weighted Bergman shift, Hardy shift, etc., satisfy the regularity condition. Moreover, at the end of the article, we solve [see Problems 1 and 2 in Garcia et al. (2025)].

  • Square roots of weighted shifts of multiplicity two

  • Part of
  • Chanaka Kottegoda, Trieu Le, Tomas Miguel Rodriguez
  • Journal:
    Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
    Published online by Cambridge University Press:
    23 December 2022, pp. 791-807
    Print publication:
    September 2023
    • Article
      • You have access
      • Open access
    • PDF
    • HTML
    • Export citation

  • Given a weighted shift T of multiplicity two, we study the set $\sqrt {T}$ of all square roots of T. We determine necessary and sufficient conditions on the weight sequence so that this set is non-empty. We show that when such conditions are satisfied, $\sqrt {T}$ contains a certain special class of operators. We also obtain a complete description of all operators in $\sqrt {T}$.

  • A NOTE ON POSITIVE ${\mathcal{A}}{\mathcal{N}}$ OPERATORS

  • Part of
  • IAN DOUST
  • Journal:
    Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
    Published online by Cambridge University Press:
    26 December 2018, pp. 129-130
    Print publication:
    August 2019
    • Article
      • You have access
    • PDF
    • Export citation

  • We show that positive absolutely norm attaining operators can be characterised by a simple property of their spectra. This result clarifies and simplifies a result of Ramesh. As an application we characterise weighted shift operators which are absolutely norm attaining.