Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T05:21:44.087Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence and Asymptotic Behavior of Positive Solutions for Variable Exponent Elliptic Systems

Published online by Cambridge University Press:  21 December 2015

Honghui Yin  and
Zuodong Yang
Honghui Yin
Affiliation:
School of Mathematical Sciences, Huaiyin Normal University, Jiangsu 223001, China
Zuodong Yang*
Affiliation:
School of Teacher Education, Nanjing Normal University, Nanjing 210097, China Institute of Mathematics, School of Mathematical Sciences, Nanjing Normal University, Nanjing 210023, China
*
*Corresponding author. Email:yinhh@hytc.edu.cn (H. H. Yin), zdyang_jin@263.net (Z. D. Yang)
Get access

Abstract

In this paper, our main purpose is to establish the existence of positive solution of the following system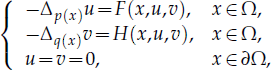 where 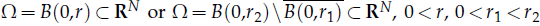are constants. F(x,u,υ) = λp(x)[g(x)a(u)+f(υ)], H(x,u,υ)=θq(x)[g1(x)b(υ)+h(u)], λ, θ>0 are parameters, p(x), q(x) are radial symmetric functions, 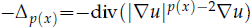is called p(x)-Laplacian. We give the existence results and consider the asymptotic behavior of the solutions. In particular, we do not assume any symmetric condition, and we do not assume any sign condition on F(x,0,0) and H(x,0,0) either.

Keywords

35J6035J62Positive solutionp(x)-Laplacianasymptotic behaviorsub-supersolution
Type
Research Article
Information
Advances in Applied Mathematics and Mechanics , Volume 8 , Issue 1 , February 2016 , pp. 19 - 36
Copyright
Copyright © Global-Science Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Acerbi, E. and Mingione, G., Regularity results for a class of functional with nonstandard growth, Arch. Ration. Mech. Anal., 156 (2001), pp. 121–140.Google Scholar
[2]Bendahmanea, M. and Wittbold, P., Renormalized solutions for nonlinear elliptic equations with variable exponents and L1 data, Nonlinear Anal., 70 (2009), pp. 567–583.Google Scholar
[3]Acerbi, E. and Mingione, G., Regularity results for stationary electro-rheological fluids, Arch. Ration. Mech. Anal., 164 (2002), pp. 213–259.Google Scholar
[4]Chen, C. H., On positive weak solutions for a class of quasilinear elliptic systems, Nonlinear Anal., 62 (2005), pp. 751–756.Google Scholar
[5]Fan, X. L., Global C1,α regularity for variable exponent elliptic equations in divergence form, J. Differential Equations, 235 (2007), pp. 397–417.Google Scholar
[6]Fan, X. L. and Zhao, D., On the spaces Lp(x)(Ω) and Wm,p(x)(Ω), J. Math. Anal. Appl., 263 (2001), pp. 424–446.Google Scholar
[7]Fan, X. L., Wu, H. Q. and Wang, F. Z., Hartman-type results for p(t)-Laplacian systems, Nonlinear Anal., 52 (2003), pp. 585–594.CrossRefGoogle Scholar
[8]Fan, X. L., Zhao, Y. Z. and Zhao, D., Compact imbedding theorems with symmetry of Strauss-Lions type for the spaces W1,p(x), J. Math. Anal. Appl., 255 (2001), pp. 333–348.Google Scholar
[9]Fan, X. L. and Zhang, Q. H., Existence of solutions for p(x)-Laplacian Dirichlet problem, Nonlinear Anal., 52 (2003), pp. 1843–1852.CrossRefGoogle Scholar
[10]Fan, X. L., On the sub-supersolution method for p(x)-Laplacian equations, J. Math. Anal. Appl., 330 (2007), pp. 665–682.CrossRefGoogle Scholar
[11]Fan, X. L., Zhang, Q. H. and Zhao, D., Eigenvalues of p(x)-Laplacian Dirichlet problem, J. Math. Anal. Appl., 302 (2005), pp. 306–317.CrossRefGoogle Scholar
[12]Hai, D. D. and Shivaji, R., An existence result on positive solutions of p-Laplacian systems, Nonlinear Anal., 56 (2004), pp. 1007–1010.Google Scholar
[13]Ei Hamidi, A., Existence results to elliptic systems with nonstandard growth con-ditions, J. Math. Anal. Appl., 300 (2004), pp. 30–42.Google Scholar
[14]Kováčik, O. and Rákosnik, J., On the spaces Lp(x)(Ω) and Wk,p(x)(Ω), Czechoslovak Math. J., 41 (1991), pp. 592–618.Google Scholar
[15]Lions, P. L., On the existence of positive solutions of semilinear elliptic equations, SIAM Rev., 24 (1982), pp. 441–467.Google Scholar
[16]Oruganti, S., Shi, J. and Shivaji, R., Diffusive equations with constant yield harvesting, I: steady states, Trans. Amer. Math. Soc., 354 (2002), pp. 3601–3619.CrossRefGoogle Scholar
[17]Rúzicka, M., Electro-Rheological Fluids: Modeling and Mathematical Theory, Lecture Notes in Math.,Vol. 1784, Springer-Verlag, Berlin, 2000.CrossRefGoogle Scholar
[18]Sanko, S. G., Denseness of in the generalized Sobolev spaces Wm,p(x)(RN), Dokl. Ross. Akad. Nauk., 369(4) (1999), pp. 451–454.Google Scholar
[19]Yin, H. H. and Yang, Z. D., Existence and nonexistence of entire positive solutions for quasilinear systems with singular and super-linear terms, Differential Equations Appl., 2(2) (2010), pp. 241–249.Google Scholar
[20]Yin, H. H., Existence results for classes of quasilinear elliptic systems with sign-changing weight, Int. J. Nonlinear Sci., 10 (2010), pp. 53–60.Google Scholar
[21]Zhang, Q. H., Existence of positive solutions for a class of p(x)-Laplacian systems, J. Math. Anal. Appl., 333 (2007), pp. 591–603.CrossRefGoogle Scholar
[22]Zhang, Q. H., Existence of positive solutions for elliptic systems with nonstandard p(x)-growth conditions via sub-supersolution method, Nonlinear Anal., 67 (2007), pp. 1055–1067.Google Scholar
[23]Zhang, Q. H., Existence and asymptotic behavior of positive solutions for a variable exponent elliptic system without variational structure, Nonlinear Anal., 72 (2010), pp. 354–363.CrossRefGoogle Scholar
[24]Zhang, Q. H., Existence of radial solutions for p(x)-Laplacian equations in RN, J. Math. Anal. Appl., 315(2) (2006), pp. 506–516.Google Scholar
[25]Zhang, Q. H., A strong maximum principle for differential equations with nonstand p(x)-growth conditions, J. Math. Anal. Appl., 312(1) (2005), pp. 24–32.Google Scholar
[26]Zhang, Q. H., Existence and asymptotic behavior of positive solutions for variable exponent elliptic systems, Nonlinear Anal., 70 (2009), 305–316.CrossRefGoogle Scholar
[27]Zhikov, V. V., Averaging of functional of the calculus of variations and elasticity theory, Math. USSR Izv., 29 (1987), pp. 33–36.Google Scholar