Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Szczotka, Władysław
1997.
Asymptotic stationarity of queueing processes.
Journal of Applied Probability,
Vol. 34,
Issue. 04,
p.
1041.

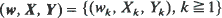 where
where 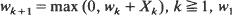 is a vector in
is a vector in 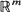 with non-negative coordinates,
with non-negative coordinates, 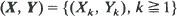 is an
is an 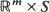 -valued process,
-valued process, 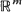 are meant in the coordinate-wise sense. It is shown that a type of asymptotic stationarity of (
are meant in the coordinate-wise sense. It is shown that a type of asymptotic stationarity of (