Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Prakasa Rao, B. L. S.
and
Ramachandran, B.
1983.
On a characterization of symmetric stable processes.
Aequationes Mathematicae,
Vol. 26,
Issue. 1,
p.
113.
Cambanis, Stamatis
1988.
Random filters which preserve the stability of random inputs.
Advances in Applied Probability,
Vol. 20,
Issue. 2,
p.
275.
Cambanis, Stamatis
1988.
Random filters which preserve the stability of random inputs.
Advances in Applied Probability,
Vol. 20,
Issue. 02,
p.
275.
1992.
Identifiability in Stochastic Models.
p.
229.
Prakasa, B. L. S. Rao
1999.
On a Characterization of Stochastic Processes by the Absolute Moments of Stochastic Integrals.
Theory of Probability & Its Applications,
Vol. 43,
Issue. 1,
p.
144.
Rao, B.L.S. Prakasa
2001.
Stochastic Processes: Theory and Methods.
Vol. 19,
Issue. ,
p.
643.

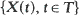 be a continuous homogeneous stochastic process with independent increments. A review of the recent work on the characterization of Wiener and stable processes and connected results through stochastic integrals is presented. No proofs are given but appropriate references are mentioned.
be a continuous homogeneous stochastic process with independent increments. A review of the recent work on the characterization of Wiener and stable processes and connected results through stochastic integrals is presented. No proofs are given but appropriate references are mentioned.