Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T07:30:26.285Z Has data issue: false hasContentIssue false
  • English
  • Français

Conditioned Limit Theorems for the Difference of Waiting Time and Queue Length

Part of: Special processes

Published online by Cambridge University Press:  01 July 2016

Władysław Szczotka  and
Krzysztof Topolski
Władysław Szczotka
Affiliation:
Wrocław University
Krzysztof Topolski*
Affiliation:
Wrocław University
*
* Postal address for both authors: Mathematical Institute of Wrocław University, Pl. Grunwałdzki 2/4, 50–384 Wrocław, Poland.
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider the GI/G/1 queueing system with traffic intensity 1 and let wk and lk denote the actual waiting time of the kth unit and the number of units present in the system at the kth arrival including the kth unit, respectively. Furthermore let τ denote the number of units served during the first busy period and μ the intensity of the service. It is shown that 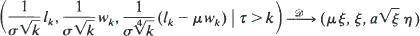as k →∞, where a is some known constant, 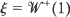, , 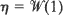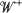and 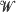are independent, 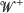is a Brownian meander and 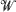is a Wiener process. A similar result is also given for the difference of virtual waiting time and queue length processes. These results are also extended to a wider class of queueing systems than GI/G/1 queues and a scheme of series of queues.

Keywords

SINGLE-SERVER QUEUEING SYSTEMBUSY PERIODBROWNIAN MEANDERWIENER PROCESSCONDITIONED LIMIT THEOREM

MSC classification

Primary: 60K25: Queueing theory
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 26 , Issue 1 , March 1994 , pp. 242 - 257
Copyright
Copyright © Applied Probability Trust 1994 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Billingsley, P. B. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
[2] Bolthausen, E. (1976) On a functional central limit theorem for random walks conditioned to stay positive. Ann. Prob. 4, 480–485.CrossRefGoogle Scholar
[3] Durrett, R. T., Iglehart, D. L. and Miller, D. R. (1977) Weak convergence to Brownian meander and Brownian excursion. Ann. Prob. 5, 117–129.Google Scholar
[4] Durrett, R. T. and Iglehart, D. L. (1977) Functionals of Brownian meander and Brownian excursion. Ann. Prob. 5, 130–135.Google Scholar
[5] Hooghiemstra, G. and Kennedy, D. P. (1984) Conditioned limit theorems and heavy traffic. Ann. Prob. 12, 631–634.CrossRefGoogle Scholar
[6] Iglehart, D. L. (1974) Functional central limit theorems for random walks conditioned to stay positive. Ann. Prob. 2, 608–619.Google Scholar
[7] Lindvall, T. (1973) Weak convergence of probability measures and random functions in function space D(8). J. Appl. Prob. 10, 109–121.Google Scholar
[8] Massey, A. W. and Whitt, W. (1992) Unstable asymptotics for nonstationary queues. AT&T Bell Laboratories, Murray Hill.Google Scholar
[9] Serfozo, R. F., Szczotka, W. and Topolski, K. (1992) Relating the waiting time in a heavy traffic queueing system to the queue length. Stoch. Proc. Appl. To appear.Google Scholar
[10] Szczotka, W. (1986) Stationary representation of queues. II. Adv. Appl. Prob. 18, 849–859.Google Scholar
[11] Szczotka, W. (1992) A distributional form of Little's law in heavy traffic. Ann. Prob. 20, 790–800.Google Scholar
[12] Szczotka, W. and Topolski, K. (1989) Conditioned limit theorem for the pair of waiting time and queue line processes. Queueing Systems 5, 393–400.Google Scholar
[13] Topolski, K. (1990) Conditioned Limit Theorem for Random Walk and their Application to Queueing Theory. Doctoral Thesis, Mathematical Institute, The University of Wroclaw.Google Scholar
[14] Topolski, K. (1991) Conditioned functions central limit theorem for random partial sums. Prob. Math. Statist. 11, 247–252.Google Scholar
[15] Whitt, W. (1992) A review of L = ?W and extensions. Queueing Systems. To appear.Google Scholar