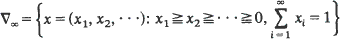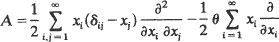Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shiga, Tokuzo
1982.
Wandering phenomena in infinite-allelic diffusion models.
Advances in Applied Probability,
Vol. 14,
Issue. 03,
p.
457.
Sawyer, Stanley
1983.
A stability property of the Ewens sampling formula.
Journal of Applied Probability,
Vol. 20,
Issue. 03,
p.
449.
Dawson, Donald A.
and
Hochberg, Kenneth J.
1983.
Qualitative behavior of a selectively neutral allelic model.
Theoretical Population Biology,
Vol. 23,
Issue. 1,
p.
1.
Sato, Ken-Iti
1983.
Limit diffusions of some stepping-stone models.
Journal of Applied Probability,
Vol. 20,
Issue. 03,
p.
460.
1986.
Markov Processes.
p.
508.
Donnelly, Peter
1986.
Partition structures, Polya urns, the Ewens sampling formula, and the ages of alleles.
Theoretical Population Biology,
Vol. 30,
Issue. 2,
p.
271.
Hoppe, Fred M.
1987.
The sampling theory of neutral alleles and an urn model in population genetics.
Journal of Mathematical Biology,
Vol. 25,
Issue. 2,
p.
123.
Ethier, S. N.
and
Kurtz, T. G.
1987.
Stochastic Methods in Biology.
Vol. 70,
Issue. ,
p.
72.
Cox, J. Theodore
and
Griffeath, David
1987.
Percolation Theory and Ergodic Theory of Infinite Particle Systems.
Vol. 8,
Issue. ,
p.
73.
Donnelly, P. J.
and
Tavaré, S.
1987.
Stochastic Methods in Biology.
Vol. 70,
Issue. ,
p.
27.
Donnelly, Peter
and
Tavar�, Simon
1987.
The population genealogy of the infinitely-many neutral alleles model.
Journal of Mathematical Biology,
Vol. 25,
Issue. 4,
p.
381.
Ethier, S. N.
1990.
The infinitely-many-neutral-alleles diffusion model by ages.
Advances in Applied Probability,
Vol. 22,
Issue. 01,
p.
1.
Ewens, W. J.
1990.
Mathematical and Statistical Developments of Evolutionary Theory.
p.
177.
Ethier, S. N.
and
Griffiths, R. C.
1990.
The neutral two-locus model as a measure-valued diffusion.
Advances in Applied Probability,
Vol. 22,
Issue. 4,
p.
773.
Ethier, S. N.
1990.
The distribution of the frequencies of age-ordered alleles in a diffusion model.
Advances in Applied Probability,
Vol. 22,
Issue. 03,
p.
519.
Schmuland, B.
1991.
A result on the infinitely many neutral alleles diffusion model.
Journal of Applied Probability,
Vol. 28,
Issue. 02,
p.
253.
Ethier, S. N.
1992.
Eigenstructure of the infinitely-many-neutral-alleles diffusion model.
Journal of Applied Probability,
Vol. 29,
Issue. 03,
p.
487.
Ethier, S. N.
and
Kurtz, Thomas G.
1993.
Fleming–Viot Processes in Population Genetics.
SIAM Journal on Control and Optimization,
Vol. 31,
Issue. 2,
p.
345.
Ethier, S.N.
and
Kurtz, Thomas G.
1994.
Convergence to Fleming-Viot processes in the weak atomic topology.
Stochastic Processes and their Applications,
Vol. 54,
Issue. 1,
p.
1.
Dawson, Donald A.
Greven, Andreas
and
Vaillancourt, Jean
1995.
Equilibria and quasiequilibria for infinite collections of interacting Fleming-Viot processes.
Transactions of the American Mathematical Society,
Vol. 347,
Issue. 7,
p.
2277.