Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Denuit, Michel
and
Müller, Alfred
2004.
Encyclopedia of Actuarial Science.
Sancetta, Alessio
2007.
Weak Convergence of Laws on ℝ
K
with Common Marginals.
Journal of Theoretical Probability,
Vol. 20,
Issue. 2,
p.
371.
Li, Ke
Zhou, Wanlei
Li, Ping
Hai, Jing
and
Liu, Jianwen
2009.
Distinguishing DDoS Attacks from Flash Crowds Using Probability Metrics.
p.
9.
Sriperumbudur, Bharath K.
Fukumizu, Kenji
Gretton, Arthur
Scholkopf, Bernhard
and
Lanckriet, Gert R. G.
2010.
Non-parametric estimation of integral probability metrics.
p.
1428.
Kumar, Abhishek
and
Hansen, John H. L.
2010.
A kernel mean matching approach for environment mismatch compensation in speech recognition.
p.
4582.
Halder, Abhishek
and
Bhattacharya, Raktim
2011.
Model validation: A probabilistic formulation.
p.
1692.
Sugiyama, Masashi
Suzuki, Taiji
Itoh, Yuta
Kanamori, Takafumi
and
Kimura, Manabu
2011.
Least-squares two-sample test.
Neural Networks,
Vol. 24,
Issue. 7,
p.
735.
Joshi, Sarang
Kommaraji, Raj Varma
Phillips, Jeff M.
and
Venkatasubramanian, Suresh
2011.
Comparing distributions and shapes using the kernel distance.
p.
47.
Muñoz, Alberto
Martos, Gabriel
Arriero, Javier
and
Gonzalez, Javier
2012.
Artificial Neural Networks and Machine Learning – ICANN 2012.
Vol. 7553,
Issue. ,
p.
271.
Sriperumbudur, Bharath K.
Fukumizu, Kenji
Gretton, Arthur
Schölkopf, Bernhard
and
Lanckriet, Gert R. G.
2012.
On the empirical estimation of integral probability metrics.
Electronic Journal of Statistics,
Vol. 6,
Issue. none,
Olivetti, Emanuele
Benozzo, Danilo
Kia, Seyed Mostafa
Ellero, Marta
and
Hartmann, Thomas
2013.
The Kernel Two-Sample Test vs. Brain Decoding.
p.
128.
Sejdinovic, Dino
Sriperumbudur, Bharath
Gretton, Arthur
and
Fukumizu, Kenji
2013.
Equivalence of distance-based and RKHS-based statistics in hypothesis testing.
The Annals of Statistics,
Vol. 41,
Issue. 5,
Muñoz, Alberto
Martos, Gabriel
and
González, Javier
2013.
Progress in Pattern Recognition, Image Analysis, Computer Vision, and Applications.
Vol. 8258,
Issue. ,
p.
222.
Denuit, Michel
and
Müller, Alfred
2014.
Wiley StatsRef: Statistics Reference Online.
Höller, Yvonne
Thomschewski, Aljoscha
Bergmann, Jürgen
Kronbichler, Martin
Crone, Julia S.
Schmid, Elisabeth V.
Butz, Kevin
Höller, Peter
Nardone, Raffaele
and
Trinka, Eugen
2014.
Connectivity biomarkers can differentiate patients with different levels of consciousness.
Clinical Neurophysiology,
Vol. 125,
Issue. 8,
p.
1545.
Wilson, Craig
Veeravalli, Venugopal
and
Nedic, Angelia
2014.
Dynamic stochastic optimization.
p.
173.
Ning, Lipeng
and
Georgiou, Tryphon T.
2014.
Metrics for Matrix-valued Measures via Test Functions.
p.
2642.
Halder, Abhishek
and
Bhattacharya, Raktim
2014.
Probabilistic model validation for uncertain nonlinear systems.
Automatica,
Vol. 50,
Issue. 8,
p.
2038.
Gangeh, Mehrdad J.
Sadeghi-Naini, Ali
Diu, Michael
Tadayyon, Hadi
Kamel, Mohamed S.
and
Czarnota, Gregory J.
2014.
Categorizing Extent of Tumor Cell Death Response to Cancer Therapy Using Quantitative Ultrasound Spectroscopy and Maximum Mean Discrepancy.
IEEE Transactions on Medical Imaging,
Vol. 33,
Issue. 6,
p.
1390.
Da Veiga, Sebastien
2015.
Global sensitivity analysis with dependence measures.
Journal of Statistical Computation and Simulation,
Vol. 85,
Issue. 7,
p.
1283.

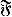 of functions and probability measures
of functions and probability measures 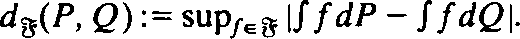 A unified study of such
A unified study of such 