Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T16:08:52.664Z Has data issue: false hasContentIssue false
  • English
  • Français

Rate of convergence for computing expectations of stopping functionals of an α-mixing process

Part of: Limit theorems

Published online by Cambridge University Press:  01 July 2016

Mohamed Ben Alaya  and
Gilles Pagès
Mohamed Ben Alaya*
Affiliation:
LAGA URA 742 and CERMICS
Gilles Pagès*
Affiliation:
Université Paris 12 and Univ. P. & M. Curie
*
∗ Postal address: (1) LAGA URA 742, Institut Galilée Université Paris 13, Avenue J.B. Clément, 93430 Villetaneuse, France, (2) CERMICS, ENPC, 6-8 av. Blaise Pascal, cité Descartes, Champs-sur-Marne, F-77455 Marne-la-vallée Cedex 2, France. Email address: mba@erato.enpc.fr
∗∗ Postal address: (1) Dept. Math., Univ. Paris 12, Fac. Sciences, 61 av. Général de Gaulle, F-94010 Créteil Cedex, France, (2) Labo. Probabilités, URA 224, Univ. P. & M. Curie, Tour 56, 4, pl. Jussieu, F-75252 Paris Cedex 05, France. Email address: gpa@ccr.jussieu.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

The shift method consists in computing the expectation of an integrable functional F defined on the probability space ((ℝd)N, B(ℝd)⊗N, μ⊗N) (μ is a probability measure on ℝd) using Birkhoff's Pointwise Ergodic Theorem, i.e.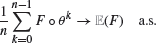

as n → ∞, where θ denotes the canonical shift operator. When F lies in L2(FT, μ⊗N) for some integrable enough stopping time T, several weak (CLT) or strong (Gàl-Koksma Theorem or LIL) converging rates hold. The method successfully competes with Monte Carlo. The aim of this paper is to extend these results to more general probability distributions P on ((ℝd)N, B(ℝd)⊗N), namely when the canonical process (Xn)n∊N is P-stationary, α-mixing and fulfils Ibragimov's assumption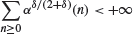

for some δ > 0. One application is the computation of the expectation of functionals of an α-mixing Markov Chain, under its stationary distribution Pν. It may both provide a better accuracy and save the random number generator compared to the usual Monte Carlo or shift methods on independent innovations.

Keywords

α-mixing processMonte Carlo methodrate of convergence

MSC classification

Primary: 60F05: Central limit and other weak theorems 60F15: Strong theorems 60F17: Functional limit theorems; invariance principles
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 30 , Issue 2 , June 1998 , pp. 425 - 448
Copyright
Copyright © Applied Probability Trust 1998 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Alaya, M. B. (1992). Les théorèmes ergodiques en simulation. , Thèse de l'École Nationale des Ponts et Chaussées.Google Scholar
[2] Alaya, M. B. (1993). On the simulation of expectations of random variables depending on a stopping time. Stoch. Analysis Appl. 11, 133–153.Google Scholar
[3] Billingsley, P. (1968). Convergence of Probability Measures. Wiley, New York.Google Scholar
[4] Bouleau, N. (1990). On effective computation of expectations in large or infinite dimension. J. Comp. Appl. Math. 31, 23–34. North-Holland.Google Scholar
[5] Bouleau, N. (1991). On numerical integration by the shift and application to Wiener space. Acta Appl. Math. 25, 201–220.Google Scholar
[6] Bouton, C. and Pagès, G. (1994). Convergence in distribution of the one-dimensional Kohonen algorithms when the stimuli are not uniform. Adv. Appl. Prob. 26, 80–103.Google Scholar
[7] Doukhan, P. (1994). Mixing, Properties and Examples. Lecture Notes in Statistics, volume 85. Springer, Berlin.Google Scholar
[8] Doukhan, P., Massart, P. and Rio, E. (1994). The functional central limit theorem for stationary mixing processes. Ann. Inst. H. Poincaré Probab. Statist. 30, 63–82.Google Scholar
[9] Duflo, M. (1990). Méthodes récursives aléatoires, Masson, Paris. (In English, Random Iterative Models, Springer, New-York, 1997.)Google Scholar
[10] Fort, J. C. and Pagès, G. (1996). Symptotic behavior of a Markovian stochastic algorithm with constant step. To appear in SIAM J. Control Optimization.Google Scholar
[11] Gàl, I. S. and Koksma, J. F. (1950). Sur l'ordre de grandeur des fonctions sommables. Indigationes Math. 12, 192–207.Google Scholar
[12] Hall, P. and Heyde, C. C. (1980). Martingale Limit Theory and its Applications. Academic Press.Google Scholar
[13] Krengel, U. (1985). Ergodic Theorems. de Gruyter Studies in Mathematics, Berlin, New York.Google Scholar
[14] Lamberton, D. and Pagès, G. (1996). On the critical points of the 1-dimensional Competitive Learning Vector Quantization Algorithm. Proc. ESANN '96. Bruges (Belgium), pp. 97–102.Google Scholar
[15] Pagès, G., (1993). Voronoï tessellation, space quantization algorithm and numerical integration. Proc. ESANN '93, ed. Verleysen, M.. Bruxelles, pp. 221–228.Google Scholar
[16] Pagès, G., Numerical integration by space quantization. To appear in J. Appl. Comp. Math.Google Scholar
[17] Philipp, W. and Stout, W. (1975). Almost sure invariance principles for partial sums of weakly dependent variables. Mem. Am. Math. Soc. 61.Google Scholar
[18] Rio, E. (1995). The functional Law of the Iterated Logarithm for stationary strongly mixing sequences. Ann. Prob. 23, 1188–1203.Google Scholar
[19] Robert, C. P. Convergence assessments for Markov Chains Monte Carlo Methods. Technical Report INSEE no. 9347.Google Scholar