Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Taylor, Robert L.
and
Inoue, Hiroshi
1997.
Random Sets.
Vol. 97,
Issue. ,
p.
347.
Dozzi, Marco
Merzbach, Ely
and
Schmidt, Volker
2001.
Limit Theorems for Sums of Random Fuzzy Sets.
Journal of Mathematical Analysis and Applications,
Vol. 259,
Issue. 2,
p.
554.
Molchanov, Ilya
2017.
Theory of Random Sets.
Vol. 87,
Issue. ,
p.
1.
Molchanov, Ilya
2017.
Theory of Random Sets.
Vol. 87,
Issue. ,
p.
225.

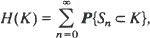
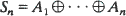 are Minkowski (element-wise) sums of i.i.d. random compact convex sets. In this paper we determine the limit of
are Minkowski (element-wise) sums of i.i.d. random compact convex sets. In this paper we determine the limit of 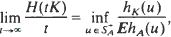
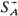 is the set of all unit vectors
is the set of all unit vectors 