Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-13T23:17:07.329Z Has data issue: false hasContentIssue false
  • English
  • Français

An ergodic theorem for asymptotically periodic time-inhomogeneous Markov processes, with application to quasi-stationarity with moving boundaries

Part of: Limit theorems Markov processes

Published online by Cambridge University Press:  08 March 2023

William Oçafrain
William Oçafrain*
Affiliation:
Université de Lorraine
*
*Postal address: IECL, UMR 7502, F-54000, Nancy, France. Email address: w.ocafrain@hotmail.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper deals with ergodic theorems for particular time-inhomogeneous Markov processes, whose time-inhomogeneity is asymptotically periodic. Under a Lyapunov/minorization condition, it is shown that, for any measurable bounded function f, the time average 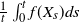$\frac{1}{t} \int_0^t f(X_s)ds$ converges in 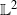$\mathbb{L}^2$ towards a limiting distribution, starting from any initial distribution for the process 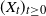$(X_t)_{t \geq 0}$ . This convergence can be improved to an almost sure convergence under an additional assumption on the initial measure. This result is then applied to show the existence of a quasi-ergodic distribution for processes absorbed by an asymptotically periodic moving boundary, satisfying a conditional Doeblin condition.

Keywords

Ergodic theoremlaw of large numberstime-inhomogeneous Markov processesquasi-stationarityquasi-ergodic distributionmoving boundaries

MSC classification

Primary: 60J25: Continuous-time Markov processes on general state spaces 60F25: $L^p$-limit theorems 60J55: Local time and additive functionals
Secondary: 60J60: Diffusion processes 60J65: Brownian motion 60J70: Applications of Brownian motions and diffusion theory (population genetics, absorption problems, etc.)
Type
Original Article
Information
Advances in Applied Probability , Volume 55 , Issue 2 , June 2023 , pp. 672 - 700
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bansaye, V., Cloez, B. and Gabriel, P. (2020). Ergodic behavior of non-conservative semigroups via generalized Doeblin’s conditions. Acta Appl. Math. 166, 29–72.CrossRefGoogle Scholar
Breyer, L. and Roberts, G. (1999). A quasi-ergodic theorem for evanescent processes. Stoch. Process. Appl. 84, 177–186.CrossRefGoogle Scholar
Cattiaux, P., Christophe, C. and Gadat, S. (2016). A stochastic model for cytotoxic T lymphocyte interaction with tumor nodules. Preprint.Google Scholar
Champagnat, N., Oçafrain, W. and Villemonais, D. (2021). Quasi-stationarity for time-(in)homogeneous Markov processes absorbed by moving boundaries through Lyapunov criteria. In preparation.Google Scholar
Champagnat, N. and Villemonais, D. (2016). Exponential convergence to quasi-stationary distribution and Q-process. Prob. Theory Relat. Fields 164, 243–283.CrossRefGoogle Scholar
Champagnat, N. and Villemonais, D. (2017). General criteria for the study of quasi-stationarity. Preprint. Available at https://arxiv.org/abs/1712.08092.Google Scholar
Champagnat, N. and Villemonais, D. (2017). Uniform convergence of conditional distributions for absorbed one-dimensional diffusions. Adv. Appl. Prob. 50, 178–203.CrossRefGoogle Scholar
Champagnat, N. and Villemonais, D. (2017). Uniform convergence to the Q-process. Electron. Commun. Prob. 22, paper no. 33, 7 pp.CrossRefGoogle Scholar
Champagnat, N. and Villemonais, D. (2018). Uniform convergence of penalized time-inhomogeneous Markov processes. ESAIM Prob. Statist. 22, 129–162.CrossRefGoogle Scholar
Chen, J. and Jian, S. (2018). A deviation inequality and quasi-ergodicity for absorbing Markov processes. Ann. Mat. Pura Appl. 197, 641–650.CrossRefGoogle Scholar
Collet, P., Martínez, S. and San Martín, J. (2013). Quasi-Stationary Distributions: Markov Chains, Diffusions and Dynamical Systems. Springer, Berlin, Heidelberg.CrossRefGoogle Scholar
Colonius, F. and Rasmussen, M. (2021). Quasi-ergodic limits for finite absorbing Markov chains. Linear Algebra Appl. 609, 253–288.CrossRefGoogle Scholar
Darroch, J. N. and Seneta, E. (1965). On quasi-stationary distributions in absorbing discrete-time finite Markov chains. J. Appl. Prob. 2, 88–100.CrossRefGoogle Scholar
Devroye, L., Mehrabian, A. and Reddad, T. (2018). The total variation distance between high-dimensional Gaussians. Preprint. Available at https://arxiv.org/abs/1810.08693.Google Scholar
Hairer, M. and Mattingly, J. C. (2011). Yet another look at Harris’ ergodic theorem for Markov chains. In Seminar on Stochastic Analysis, Random Fields and Applications VI, Birkhäuser, Basel, pp. 109–117.CrossRefGoogle Scholar
He, G. (2018). A note on the quasi-ergodic distribution of one-dimensional diffusions. C. R. Math. Acad. Sci. Paris 356, 967–972.CrossRefGoogle Scholar
He, G., Yang, G. and Zhu, Y. (2019). Some conditional limiting theorems for symmetric Markov processes with tightness property. Electron. Commun. Prob. 24, paper no. 60, 11 pp.CrossRefGoogle Scholar
He, G., Zhang, H. and Zhu, Y. (2019). On the quasi-ergodic distribution of absorbing Markov processes. Statist. Prob. Lett. 149, 116–123.CrossRefGoogle Scholar
Hening, A. and Nguyen, D. H. (2018). Stochastic Lotka-Volterra food chains. J. Math. Biol. 77, 135–163.CrossRefGoogle ScholarPubMed
Höpfner, R. and Kutoyants, Y. (2010). Estimating discontinuous periodic signals in a time inhomogeneous diffusion. Statist. Infer. Stoch. Process. 13, 193–230.CrossRefGoogle Scholar
Höpfner, R., Löcherbach, E. and Thieullen, M. (2016). Ergodicity and limit theorems for degenerate diffusions with time periodic drift. Application to a stochastic Hodgkin–Huxley model. ESAIM Prob. Statist. 20, 527–554.CrossRefGoogle Scholar
Höpfner, R., Löcherbach, E. and Thieullen, M. (2016). Ergodicity for a stochastic Hodgkin–Huxley model driven by Ornstein–Uhlenbeck type input. Ann. Inst. H. Poincaré Prob. Statist. 52, 483–501.CrossRefGoogle Scholar
Méléard, S. and Villemonais, D. (2012). Quasi-stationary distributions and population processes. Prob. Surveys 9, 340–410.CrossRefGoogle Scholar
Oçafrain, W. (2018). Quasi-stationarity and quasi-ergodicity for discrete-time Markov chains with absorbing boundaries moving periodically. ALEA 15, 429–451.CrossRefGoogle Scholar
Oçafrain, W. (2020). Q-processes and asymptotic properties of Markov processes conditioned not to hit moving boundaries. Stoch. Process. Appl. 130, 3445–3476.CrossRefGoogle Scholar
Vassiliou, P.-C. (2018). Laws of large numbers for non-homogeneous Markov systems. Methodology Comput. Appl. Prob. 22, 1631–1658.CrossRefGoogle Scholar