Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T13:14:40.495Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximations for the repairman problem with two repair facilities, I: No spares

Published online by Cambridge University Press:  01 July 2016

Donald L. Iglehart  and
Austin J. Lemoine
Donald L. Iglehart
Affiliation:
Stanford University
Austin J. Lemoine*
Affiliation:
Control Analysis Corporation
*
∗ Now at Clemson University.
Get access Rights & Permissions [Opens in a new window]

Abstract

The model considered here consists of n operating units which are subject to stochastic failure according to an exponential failure time distribution. Failures can be of two types. With probability p(q) a failure is of type 1(2) and is sent to repair facility 1(2) for repair. Repair facility 1(2) operates as a 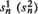-server queue with exponential repair times having parameter μ1 (μ2). The number of units waiting for or undergoing repair at each of the two facilities is a continuous-parameter Markov chain with finite state space. This paper derives limit theorems for the stationary distribution of this Markov chain as n becomes large under the assumption that both 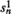and 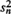grow linearly with n. These limit theorems give very useful approximations, in terms of the six parameters characterizing the model, to a distribution that would be difficult to use in practice.

Keywords

BIRTH AND DEATH PROCESSESCENTRAL LIMIT THEOREMLOCAL CENTRAL LIMIT THEOREMLOGISTICS SYSTEMSREPAIRMAN PROBLEMREVERSIBLE MARKOV CHAINSWEAK LAW OF LARGE NUMBERS
Type
Research Article
Information
Advances in Applied Probability , Volume 5 , Issue 3 , December 1973 , pp. 595 - 613
Copyright
Copyright © Applied Probability Trust 1973 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research sponsored by Office of Naval Research contract N00014-72-C-Q266 (NR-347-Q22).

References

[1] Barlow, R. E. (1962) Repairman problems. Studies in Applied Probability and Management Science. Eds. Arrow, K., Karlin, S., and Scarf, H.. Stanford University Press, Stanford, California. 18–33.Google Scholar
[2] Billingsley, P. (1968) Convergence of Probability Measures. John Wiley, New York.Google Scholar
[3] Feller, W. (1957) An Introduction to Probability Theory and its Applications. Vol. I. John Wiley, New York.Google Scholar
[4] Gnedenko, B. V., Belyaev, Yu. K. and Solovyev, A. D. (1969) Mathematical Methods of Reliability Theory. Academic Press, New York.Google Scholar
[5] Gnedenko, B. V. and Kolmogorov, A. N. (1954). Limit Distributions for Sums of Independent Random Variables. Addison-Wesley, Reading, Mass. (English translation.) Google Scholar
[6] Iglehart, D. L. (1964) Reversible competition processes. Z. Wahrscheinlichkeitsth. 2, 314–331.Google Scholar
[7] Iglehart, D. L. (1965) Limiting diffusion approximations for the many server queue and the repairman problem. J. Appl. Prob. 2, 429–441.Google Scholar
[8] Karlin, S. (1966) A First Course in Stochastic Processes. Academic Press, New York.Google Scholar
[9] Stone, C. (1967) On local and ratio limit theorems. Fifth Berkeley Symp. on Math. Statist. Prob. II (Part 2), 218–224.Google Scholar