Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T20:13:08.683Z Has data issue: false hasContentIssue false
  • English
  • Français

The asymptotic behaviour of extinction probability in the Smith–Wilkinson branching process

Part of: Markov processes

Published online by Cambridge University Press:  01 July 2016

D. R. Grey  and
Lu Zhunwei
D. R. Grey*
Affiliation:
University of Sheffield
Lu Zhunwei
Affiliation:
University of Sheffield
*
∗Postal address: Department of Probability and Statistics, The University of Sheffield, PO Box 597, Sheffield, S10 2UN, UK.
Get access Rights & Permissions [Opens in a new window]

Abstract

Under some regularity conditions, in the supercritical Smith–Wilkinson branching process it is shown that as k, the starting population size, tends to infinity, the rate of convergence of qk, the corresponding extinction probability, to zero is similar to that of:

k–θ, if there exists at least one subcritical state in the random environment space; xkk–α, if there exist only supercritical states in the random environment space; exp 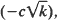, if there exists at least one critical state and the others are supercritical in the random environment space.

Here θ, x, α and c are positive constants determined by the process.

Keywords

BRANCHING PROCESS IN RANDOM ENVIRONMENTDUAL PROCESS

MSC classification

Primary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Secondary: 60J85: Applications of branching processes
Type
Research Article
Information
Advances in Applied Probability , Volume 25 , Issue 2 , June 1993 , pp. 263 - 289
Copyright
Copyright © Applied Probability Trust 1993 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

∗∗

Present address: Department of Mathematics, Physics and Mechanics, Taiyuan University of Technology, Taiyuan, Shanxi Province, People's Republic of China.

References

Agresti, A. (1974) Bounds on the extinction time distribution of a branching process. Adv. Appl. Prob. 6, 322–335.Google Scholar
Athreya, K. B. and Karlin, S. (1971) On branching processes with random environments (I), (II). Ann. Math. Statist. 42 1499–1520, 1843–1858.CrossRefGoogle Scholar
Athreya, K. B. and Ney, P. E. (1972) Branching Processes. Springer-Verlag, Berlin.Google Scholar
Bingham, N. H., Goldie, C. M. and Teugels, J. L. (1987) Regular Variation: Encyclopedia of Mathematics and its Applications. Cambridge University Press.Google Scholar
Cox, D. R. and Miller, H. D. (1965) The Theory of Stochastic Processes. Chapman and Hall, London.Google Scholar
Dittrich, P. (1990) A critical branching process in random environment. Theory Prob. Appl. 35, 560–563.Google Scholar
Feller, W. (1971) An Introducton to Probability Theory and its Applications. Vol. I, 3rd edn; Vol. II, 2nd edn. Wiley, New York.Google Scholar
Goldie, C. M. (1991) Implicit renewal theory and tails of solutions of random equations. Ann. Appl. Prob. 1, 126–166.Google Scholar
Grey, D. R. and Zhunwei, Lu (1991) Extinction probabilities of branching processes in random environments. I.M.S. Lecture Notes Monograph Series 18: Selected Proceedings of the Sheffield Symposium on Applied Probability , 205–211.Google Scholar
Kozlov, M. V. (1976) On the asymptotic behaviour of the probability of non-extinction for critical branching processes in random environment. Theory Prob. Appl. 21, 791–804.Google Scholar
Zhunwei, Lu (1991) Survival of Reproducing Populations in Random Environments. Ph.D. Thesis, University of Sheffield.Google Scholar
Smith, W. L. and Wilkinson, W. E. (1969) On branching processes in random environments. Ann. Math. Statist. 40, 814–827.Google Scholar