Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-13T05:06:19.576Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic variance for random walk Metropolis chains in high dimensions: logarithmic growth via the Poisson equation

Part of: Markov processes Limit theorems

Published online by Cambridge University Press:  15 November 2019

Aleksandar Mijatović  and
Jure Vogrinc
Aleksandar Mijatović*
Affiliation:
University of Warwick and The Alan Turing Institute
Jure Vogrinc*
Affiliation:
University of Warwick
*
* Postal address: Department of Statistics, University of Warwick, Coventry CV4 7AL, UK.
* Postal address: Department of Statistics, University of Warwick, Coventry CV4 7AL, UK.
Get access Rights & Permissions [Opens in a new window]

Abstract

There are two ways of speeding up Markov chain Monte Carlo algorithms: (a) construct more complex samplers that use gradient and higher-order information about the target and (b) design a control variate to reduce the asymptotic variance. While the efficiency of (a) as a function of dimension has been studied extensively, this paper provides the first results linking the efficiency of (b) with dimension. Specifically, we construct a control variate for a d-dimensional random walk Metropolis chain with an independent, identically distributed target using the solution of the Poisson equation for the scaling limit in [30]. We prove that the asymptotic variance of the corresponding estimator is bounded above by a multiple of 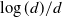$\log(d)/d$ over the spectral gap of the chain. The proof hinges on large deviations theory, optimal Young’s inequality and Berry–Esseen-type bounds. Extensions of the result to non-product targets are discussed.

Keywords

Asymptotic variancePoisson equation for diffusionsvariance reductionscaling limits of Metropolis–Hastings chainoptimal Young’s inequalityBerry–Esseen boundlarge deviations

MSC classification

Primary: 60J05: Discrete-time Markov processes on general state spaces 60J22: Computational methods in Markov chains
Secondary: 60J35: Transition functions, generators and resolvents 60F05: Central limit and other weak theorems 60F10: Large deviations
Type
Original Article
Information
Advances in Applied Probability , Volume 51 , Issue 4 , December 2019 , pp. 994 - 1026
Copyright
© Applied Probability Trust 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Assaraf, R. and Caffarel, M. (1999). Zero-variance principle for Monte Carlo algorithms. Phys. Rev. Lett. 83, 4682–4685.CrossRefGoogle Scholar
Barthe, F. (1998). Optimal Young’s inequality and its converse: a simple proof. Geom. Funct. Anal. 8, 234–242.CrossRefGoogle Scholar
Bédard, M. (2007). Weak convergence of Metropolis algorithms for non-I.I.D. target distributions. Ann. Appl. Prob. 17, 1222–1244.CrossRefGoogle Scholar
Bédard, M. and Rosenthal, J. (2008). Optimal scaling of Metropolis algorithms: heading toward general target distributions. Canad. J. Statist. 36, 483–503.CrossRefGoogle Scholar
Beskos, A., Pillai, N., Roberts, G., Sanz-Serna, J.-M. and Stuart, A. (2013). Optimal tuning of the hybrid Monte Carlo algorithm. Bernoulli 19, 1501–1534.CrossRefGoogle Scholar
Beskos, A., Roberts, G. and Stuart, A. (2009). Optimal scalings for local Metropolis–Hastings chains on nonproduct targets in high dimensions. Ann. Appl. Prob. 19, 863–898.CrossRefGoogle Scholar
Bierkens, J. and Roberts, G. (2017). A piecewise deterministic scaling limit of lifted Metropolis–Hastings in the Curie–Weiss model. Ann. Appl. Prob. 27, 846–882.CrossRefGoogle Scholar
Brooks, S., Gelman, A., Jones, G. and Meng, X.-L., eds (2011). Handbook of Markov Chain Monte Carlo (Handbooks of Modern Statistical Methods). Chapman & Hall/CRC, Boca Raton, FL.Google Scholar
Dellaportas, P. and Kontoyiannis, I. (2012). Control variates for estimation based on reversible Markov chain Monte Carlo samplers. J. R. Statist. Soc. B 74, 133–161.CrossRefGoogle Scholar
Duane, S., Kennedy, A., Pendleton, B. and Roweth, D. (1987). Hybrid Monte Carlo. Phys. Lett. B 195, 216–222.CrossRefGoogle Scholar
Duncan, A., Lelièvre, T. and Pavliotis, G. (2016). Variance reduction using nonreversible Langevin samplers. J. Statist. Phys. 163, 457.CrossRefGoogle ScholarPubMed
Durmus, A., Roberts, G. O., Vilmart, G. and Zygalakis, K. C. (2017). Fast Langevin based algorithm for MCMC in high dimensions. Ann. Appl. Prob. 27(4), 2195–2237.CrossRefGoogle Scholar
Eichelsbacher, P. and Löwe, M. (2003). Moderate deviations for i.i.d. random variables. ESAIM Prob. Statist. 7, 209–218.CrossRefGoogle Scholar
Geyer, C. (1992). Practical Markov chain Monte Carlo. Statist. Sci. 473–483.CrossRefGoogle Scholar
Henderson, S. (1997). Variance reduction via an approximating Markov process. PhD thesis, Department of Operations Research, Stanford University.Google Scholar
Jarner, S. and Hansen, E. (2000). Geometric ergodicity of Metropolis algorithms. Stoch. Process. Appl. 85, 341–361.CrossRefGoogle Scholar
Jourdain, B., Lelièvre, T. and Miasojedow, B. (2015). Optimal scaling for the transient phase of the random walk Metropolis algorithm: the mean-field limit. Ann. Appl. Prob. 25, 2263–2300.CrossRefGoogle Scholar
Kipnis, C. and Varadhan, S. R. S. (1986). Central limit theorem for additive functionals of reversible Markov processes and applications to simple exclusions. Commun. Math. Phys. 104, 1–19.CrossRefGoogle Scholar
Kolassa, J. (2006). Series Approximation Methods in Statistics (Lecture Notes Statist. 88). Springer Science & Business Media.Google Scholar
Mattingly, J., Pillai, N. and Stuart, A. (2012). Diffusion limits of the Random walk Metropolis algorithm in high dimensions. Ann. Appl. Prob. 22, 881–930.CrossRefGoogle Scholar
Meyn, S. (2008). Control Techniques for Complex Networks. Cambridge University Press, Cambridge.Google Scholar
Meyn, S. and Tweedie, R. (2009). Markov Chains and Stochastic Stability, 2nd edn. Cambridge University Press, Cambridge.CrossRefGoogle Scholar
Mijatović, A. and Vogrinc, J. (2018). On the Poisson equation for Metropolis–Hastings chains. Bernoulli 24(3), 2401–2428.CrossRefGoogle Scholar
Oates, C., Girolami, M. and Chopin, N. (2017). Control functionals for Monte Carlo integration. J. R. Statist. Soc. B 79, 695–718.CrossRefGoogle Scholar
Papamarkou, T., Mira, A. and Girolami, M. (2014). Zero variance differential geometric Markov chain Monte Carlo algorithms. Bayesian Anal. 9, 97–128.CrossRefGoogle Scholar
Pillai, N., Stuart, A. and Thiéry, A. (2012). Optimal scalings and diffusion limits for the Langevin algorithm in high dimensions. Ann. Appl. Prob. 22, 2320–2356.CrossRefGoogle Scholar
Roberts, G. and Rosenthal, J. (1997). Geometric ergodicity and hybrid Markov chains. Electron. Commun. Prob. 2 (2), 13–25.CrossRefGoogle Scholar
Roberts, G. and Rosenthal, J. (1998). Optimal scaling of discrete approximations to Langevin diffusions. J. R. Statist. Soc. B 60, 255–268.CrossRefGoogle Scholar
Roberts, G. and Rosenthal, J. (2001). Optimal scaling for various Metropolis–Hastings algorithms. Statist. Sci. 16, 351–367.CrossRefGoogle Scholar
Roberts, G., Gelman, A. and Gilks, W. R. (1997). Weak convergence and optimal scaling of random walk Metropolis algorithms. Ann. Appl. Prob. 7, 110–120.Google Scholar
Tierney, L. (1994). Markov chains for exploring posterior distributions. Ann. Statist. 22, 1701–1762.CrossRefGoogle Scholar
Williams, D. (1991). Probability with Martingales. Cambridge University Press.CrossRefGoogle Scholar