Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T10:19:44.188Z Has data issue: false hasContentIssue false
  • English
  • Français

The behavior of the ratio of a small-noise Markov chain to its deterministic approximation

Published online by Cambridge University Press:  01 July 2016

Norman Kaplan  and
Thomas Darden
Norman Kaplan*
Affiliation:
National Institute of Environmental Health Sciences
Thomas Darden*
Affiliation:
National Institute of Environmental Health Sciences
*
∗Postal address: Biometry and Risk Assessment Program, National Institute of Environmental Health Sciences, Research Triangle Park, NC 27709, USA.
∗Postal address: Biometry and Risk Assessment Program, National Institute of Environmental Health Sciences, Research Triangle Park, NC 27709, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

For each N≧1, let {XN(t, x), t≧0} be a discrete-time stochastic process with XN(0) = x. Let FN(y) = E(XN(t + 1) | XN(t) = y), and define YN(t, x) = FN(YN(t – 1, x)), t≧1 and YN(0, x) = x. Assume that in a neighborhood of the origin FN(y) = mNy(l + O(y)) where mN> 1, and define for δ> 0 and x> 0, υN(δ, x) = inf{t:xmtN>δ}. Conditions are given under which, for θ> 0 and ε> 0, there exist constants δ > 0 and L <∞, depending on εand 0, such that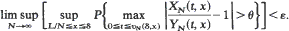 This result together with a result of Kurtz (1970), (1971) shows that, under appropriate conditions, the time needed for the stochastic process {XN(t, 1/N), t≧0} to escape a δ -neighborhood of the origin is of order log Νδ /log mN. To illustrate the results the Wright-Fisher model with selection is considered.

Keywords

MARKOV PROCESSEXIT TIMEWRIGHT-FISHER PROCESS
Type
Research Article
Information
Advances in Applied Probability , Volume 17 , Issue 4 , December 1985 , pp. 731 - 747
Copyright
Copyright © Applied Probability Trust 1985 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Athreya, K. B. and Ney, P. E. (1972) Branching Processes. Springer-Verlag, Berlin.Google Scholar
Barbour, A. D. (1974) On a functional central limit theorem for Markov population processes. Adv. Appl. Prob. 6, 21–39.CrossRefGoogle Scholar
Ewens, W. J. (1979) Mathematical Population Genetics. Springer-Verlag, Berlin.Google Scholar
Ewens, W. J. and Thomson, G. (1970) Heterozygote selective advantage. Ann. Hum. Genet., London. 33, 365–376.Google Scholar
Fisher, R. A. (1930) The Genetical Theory of Natural Selection. Clarendon Press, Oxford.CrossRefGoogle Scholar
Kaplan, N., Darden, T. and Langley, C. H. (1985) Evolution of transposable elements in Mendelian populations IV. Mutant elements and extinction. Genetics 109, 459–480.Google Scholar
Kurtz, T. G. (1970) Solutions of ordinary differential equations as limits of pure jump Markov processes. J. Appl. Prob. 7, 49–58.Google Scholar
Kurtz, T. G. (1971) Limit theorems for sequences of jump Markov processes approximating ordinary differential equations, J. Appl. Prob. 8, 344–356.Google Scholar
Lindvall, T. (1974) Limit theorems for some functionals of certain Galton-Watson branching processes. Adv. Appl. Prob. 2, 309–321.Google Scholar
Ludwig, D. (1975) Persistence of dynamical systems under random perturbations. SIAM Rev. 17, 605–640.CrossRefGoogle Scholar
Norman, F. M. (1975) Approximation of stochastic processes by Gaussian diffusions and application to Wright-Fisher genetic models. SIAM J. Appl. Math. 29, 275–242.CrossRefGoogle Scholar