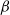 $\beta$-Delaunay tessellation: Description of the model and geometry of typical cells
$\beta$-Delaunay tessellation: Description of the model and geometry of typical cellsPublished online by Cambridge University Press: 01 August 2022
In this paper we introduce two new classes of stationary random simplicial tessellations, the so-called 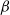 $\beta$
- and
$\beta$
- and 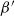 $\beta^{\prime}$
-Delaunay tessellations. Their construction is based on a space–time paraboloid hull process and generalizes that of the classical Poisson–Delaunay tessellation. We explicitly identify the distribution of volume-power-weighted typical cells, establishing thereby a remarkable connection to the classes of
$\beta^{\prime}$
-Delaunay tessellations. Their construction is based on a space–time paraboloid hull process and generalizes that of the classical Poisson–Delaunay tessellation. We explicitly identify the distribution of volume-power-weighted typical cells, establishing thereby a remarkable connection to the classes of 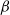 $\beta$
- and
$\beta$
- and 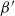 $\beta^{\prime}$
-polytopes. These representations are used to determine the principal characteristics of such cells, including volume moments, expected angle sums, and cell intensities.
$\beta^{\prime}$
-polytopes. These representations are used to determine the principal characteristics of such cells, including volume moments, expected angle sums, and cell intensities.