Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Spouge, John L.
1984.
An existence theorem for the discrete coagulation-fragmentation equations.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 96,
Issue. 2,
p.
351.
Pittel, Boris
1990.
On tree census and the giant component in sparse random graphs.
Random Structures & Algorithms,
Vol. 1,
Issue. 3,
p.
311.
Suematsu, Kazumi
and
Kohno, Minoru
2000.
Estimation of critical points of branched polymers.
Physical Review E,
Vol. 62,
Issue. 3,
p.
3944.
Fasano, A.
and
Rosso, F.
2000.
Lectures on Applied Mathematics.
p.
123.
Bertoin, Jean
2009.
Two solvable systems of coagulation equations with limited aggregations.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 26,
Issue. 6,
p.
2073.

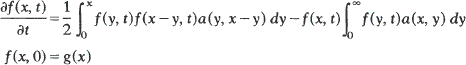
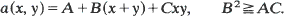
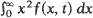 diverges corresponds to a critical branching process, while post-critical times
diverges corresponds to a critical branching process, while post-critical times 