Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T16:09:24.769Z Has data issue: false hasContentIssue false
  • English
  • Français

Central limit theorem for bifurcating markov chains under L2-ergodic conditions

Part of: Limit theorems Markov processes Nonparametric inference Parametric inference

Published online by Cambridge University Press:  15 June 2022

S. Valère Bitseki Penda Open the ORCID record for S. Valère Bitseki Penda [Opens in a new window]  and
Jean-François Delmas
S. Valère Bitseki Penda*
Affiliation:
Université Bourgogne Franche-Comté, IMB, CNRS-UMR 5584
Jean-François Delmas*
Affiliation:
CERMICS, Ecole des Ponts
*
*Postal address: Université Bourgogne Franche-Comté, IMB, CNRS-UMR 5584, 9 avenue Alain Savary, 21078 Dijon Cedex, France. Email address: simeon-valere.bitseki-penda@u-bourgogne.fr
**Postal address: CERMICS, Ecole des Ponts, 6 et 8, avenue Blaise Pascal Cité Descartes, Champs-sur-Marne 77455, Marne-la-Vallée Cedex 2, France. Email address: jean-francois.delmas@enpc.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Bifurcating Markov chains (BMCs) are Markov chains indexed by a full binary tree representing the evolution of a trait along a population where each individual has two children. We provide a central limit theorem for additive functionals of BMCs under 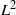$L^2$ -ergodic conditions with three different regimes. This completes the pointwise approach developed in a previous work. As an application, we study the elementary case of a symmetric bifurcating autoregressive process, which justifies the nontrivial hypothesis considered on the kernel transition of the BMCs. We illustrate in this example the phase transition observed in the fluctuations.

Keywords

Bifurcating Markov chainsbifurcating autoregressive processbinary treesfluctuations for tree-indexed Markov chainsdensity estimation

MSC classification

Primary: 60J05: Discrete-time Markov processes on general state spaces 60F05: Central limit and other weak theorems 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Secondary: 62G05: Estimation 62F12: Asymptotic properties of estimators
Type
Original Article
Information
Advances in Applied Probability , Volume 54 , Issue 4 , December 2022 , pp. 999 - 1031
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baxter, J. R. and Rosenthal, J. S. (1995). Rates of convergence for everywhere-positive Markov chains. Statist. Prob. Lett. 22, 333–338.CrossRefGoogle Scholar
Beauzany, B. (1988). Introduction to Operator Theory and Invariant Subspaces. Elsevier, Amsterdam.Google Scholar
Bitseki Penda, S. V. and Delmas, J.-F. (2020). Central limit theorem for bifurcating Markov chains. Preprint. Available at https://hal.archives-ouvertes.fr/hal-03047744.Google Scholar
Bitseki Penda, S. V. and Delmas, J.-F. (2021). Central limit theorem for bifurcating Markov chains under pointwise ergodic conditions. Preprint. Available at https://arxiv.org/abs/2012.04741v2.Google Scholar
Bitseki Penda, S. V. and Delmas, J.-F. (2022). Central limit theorem for bifurcating Markov chains under $L^{2}$ -ergodic conditions. Supplementary material. Available at https://doi.org/10.1017/apr.2022.3.Google Scholar
Bitseki Penda, S. V., Djellout, H. and Guillin, A. (2014). Deviation inequalities, moderate deviations and some limit theorems for bifurcating Markov chains with application. Ann. Appl. Prob. 24, 235–291.CrossRefGoogle Scholar
Cowan, R. and Staudte, R. (1986). The bifurcating autoregression model in cell lineage studies. Biometrics 42, 769–783.Google ScholarPubMed
Douc, R., Moulines, E., Priouret, P. and Soulier, P. (2018). Markov Chains. Springer, Cham.Google Scholar
Guyon, J. (2007). Limit theorems for bifurcating Markov chains. Application to the detection of cellular aging. Ann. Appl. Prob. 17, 1538–1569.Google Scholar
Hall, P. and Heyde, C. C. (1980). Martingale Limit Theory and Its Application. Academic Press, New York, London.Google Scholar
Supplementary material: PDF

Bitseki Penda and Delmas supplementary material

Bitseki Penda and Delmas supplementary material 1

Download Bitseki Penda and Delmas supplementary material(PDF)
PDF 279.2 KB
Supplementary material: File

Bitseki Penda and Delmas supplementary material

Bitseki Penda and Delmas supplementary material 2

Download Bitseki Penda and Delmas supplementary material(File)
File 114.3 KB
Supplementary material: File

Bitseki Penda and Delmas supplementary material

Bitseki Penda and Delmas supplementary material 3

Download Bitseki Penda and Delmas supplementary material(File)
File 40.5 KB