Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-11T01:05:03.449Z Has data issue: false hasContentIssue false
  • English
  • Français

A central limit theorem for the isotropic random sphere

Part of: Stochastic processes Limit theorems Distribution theory

Published online by Cambridge University Press:  01 July 2016

Jason J. Brown
Jason J. Brown*
Affiliation:
University of Missouri—Columbia
*
* Postal address: 5825 Saddle Seat Drive, Raleigh, NC 27606, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 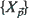be a real-valued, homogeneous, and isotropic random field indexed in 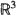. When restricted to those indices 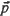with 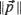, the Euclidean length of 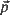, equal to r (a positive constant), then the random field 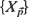resides on the surface of a sphere of radius r. Using a modified stratified spherical sampling plan (Brown (1993)) 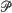on the sphere, define 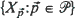to be a realization of the random process and 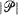to be the cardinality of 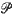. Without specifying the dependence structure of 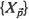nor the marginal distribution of the 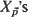, conditions for asymptotic normality of the standardized sample mean, 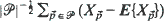, are given. The conditions on 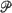and 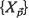are motivated by the ideas and results for dependent stationary sequences.

Keywords

ISOTROPIC RANDOM FIELDSPHERE

MSC classification

Primary: 60F05: Central limit and other weak theorems
Secondary: 62E20: Asymptotic distribution theory 60G60: Random fields
Type
Stochastic Geometry and Statistical Applications
Information
Advances in Applied Probability , Volume 27 , Issue 3 , September 1995 , pp. 642 - 651
Copyright
Copyright © Applied Probability Trust 1995 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was partially supported by NSF grant DMS-94.04130.

References

Bernstein, S. N. (1926) Sur l'extention du théorème du calcul des probabilités aux sommes de quantités dépendantes. Math. Ann. 97, 1–59.Google Scholar
Brown, J. (1993) A Finite Sampling Plan, Central Limit Theorem, and Bootstrap Algorithm for a Homogeneous and Isotropic Random Field on the 3-Dimensional Sphere. Ph.D. Thesis, Department of Statistics, The University of North Carolina at Chapel Hill, Mimeo Series #2097.Google Scholar
Dorea, C. (1972) A characterization of the multiparameter Weiner process and an application. Proc. Amer. Math. Soc. 85, 267–271.Google Scholar
Ibragimov, I. and Linnik, Y. (1971) Independent and Stationary Sequences of Random Variables. Wolters-Noordhoff, Groningen, the Netherlands.Google Scholar
Jeffreys, H. and Swirles, B. (1966) Methods of Mathematical Physics. Cambridge University Press.Google Scholar
Leonenko, L. and Yadrenko, M. (1979) Limit theorems for homogeneous and isotropic random fields. Theory Prob. Math. Statist. 21, 113–125.Google Scholar
Loeve, M. (1955) Probability Theory: Foundations and Random Sequences. Van Nostrand, New York.Google Scholar
Olea, R. (1984) Sampling design optimization for spatial functions. Math. Geol. 16, 369–392.Google Scholar
Rosenblatt, M. (1956) A central limit theorem and a strong mixing condition. Proc. Natl Acad. Sci. USA 42, 43–47.CrossRefGoogle Scholar
White, D., Kimerling, A. and Overton, S. (1992) Cartographic and geometric components of a global sampling design for environmental monitoring. Cartography and Geographic Information Systems 19, 5–22.Google Scholar
Yadrenko, M. (1983) Spectral Theory of Random Fields. Optimization Software Inc., New York.Google Scholar
Yaglom, A. (1987) Correlation Theory of Stationary and Related Random Functions I. Springer-Verlag, New York.Google Scholar