Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-10T17:37:53.916Z Has data issue: false hasContentIssue false
  • English
  • Français

Conditioned limit theorems relating a random walk to its associate, with applications to risk reserve processes and the GI/G/1 queue

Published online by Cambridge University Press:  01 July 2016

Søren Asmussen
Søren Asmussen*
Affiliation:
University of Copenhagen
*
∗Postal address: Institute of Mathematical Statistics, 5 Universitetsparken, DK-2100 Copenhagen Ø, Denmark.
Get access Rights & Permissions [Opens in a new window]

Abstract

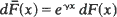Let Sn = X1 + · · · + Xn be a random walk with negative drift μ < 0, let F(x) = P(Xk ≦ x), v(u) =inf{n : Sn > u} and assume that for some γ > 0 is a proper distribution with finite mean 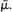Various limit theorems for functionals of X1,· · ·, Xv(u) are derived subject to conditioning upon {v(u)< ∞} with u large, showing similar behaviour as if the Xi were i.i.d. with distribution 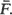For example, the deviation of the empirical distribution function from 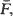properly normalised, is shown to have a limit in D, and an approximation for 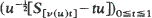by means of Brownian bridge is derived. Similar results hold for risk reserve processes in the time up to ruin and the GI/G/1 queue considered either within a busy cycle or in the steady state. The methods produce an alternate approach to known asymptotic formulae for ruin probabilities as well as related waiting-time approximations for the GI/G/1 queue. For example 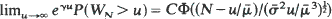uniformly in N, with WN the waiting time of the Nth customer.

Keywords

RANDOM WALKRISK RESERVE PROCESSGI/G/1 QUEUECONDITIONED LIMIT THEOREMFIRST-PASSAGE TIMEASSOCIATED RANDOM WALKEMPIRICAL DISTRIBUTION FUNCTIONBROWNIAN BRIDGERUIN PROBABILITYWAITING TIME
Type
Research Article
Information
Advances in Applied Probability , Volume 14 , Issue 1 , March 1982 , pp. 143 - 170
Copyright
Copyright © Applied Probability Trust 1982 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported in part by the tenure of a Visiting Fellowship at the Australian National University and a grant from the Danish Natural Science Research Council.

References

References

Aldous, D. J. (1978) Weak convergence of randomly indexed sequences of random variables. Math. Proc. Camb. Phil. Soc. 83, 117–126.Google Scholar
Anscombe, F. J. (1952) Large-sample theory of sequential estimation. Proc. Camb. Phil. Soc. 48, 600–607.CrossRefGoogle Scholar
Asmussen, S. (1981a) Equilibrium properties of the M/G/1 queue. Z. Wahrscheinlichkeitsth. CrossRefGoogle Scholar
Bahr, B. von (1974) Ruin probabilities expressed in terms of ladder heights. Scand. Actuarial J. 190–204.CrossRefGoogle Scholar
Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
Breiman, L. (1968) Probability. Addison-Wesley, Reading, Mass. Google Scholar
Chung, K. L. (1974) A Course in Probability Theory, 2nd edn. Academic Press, New York.Google Scholar
Cohen, J. W. (1969) The Single Server Queue. North-Holland, Amsterdam.Google Scholar
Cohen, J. W. (1976) On Regenerative Processes in Queueing Theory. Lecture Notes in Economics and Mathematical Systems 121, Springer-Verlag, Berlin.Google Scholar
Csörgö, M. and Fischler, R. (1973) Some examples and results in the theory of mixing and random-sum central limit theorems. Period Math. Hung. 3, 41–57.CrossRefGoogle Scholar
Dudley, R. M. (1978) Central limit theorems for empirical measures. Ann. Prob. 6, 899–929.Google Scholar
Durrett, R. (1980) Conditioned limit theorems for random walks with negative drift. Z. Wahrscheinlichkeitsth. 52, 277–287.Google Scholar
Eagleson, G. K. (1976) Some simple conditions for limit theorems to be mixing. Theory Prob. Appl. 21, 637–643.Google Scholar
Feller, W. (1971) An Introduction to Probability Theory and its Applications, Vol. 2, 2nd edn. Wiley, New York.Google Scholar
Grandell, J. (1977) A class of approximations of ruin probabilities. Scand. Actuarial J. Suppl. 37–52.CrossRefGoogle Scholar
Grandell, J. (1978) A remark on ‘A class of approximations of ruin probabilities’. Scand Actuarial J. 77–18.Google Scholar
Iglehart, D. L. (1969) Diffusion approximations in collective risk theory. J. Appl. Prob. 6, 285–292.CrossRefGoogle Scholar
Iglehart, D. L. (1972) Extreme values in the GI/G/1 queue. Ann. Math. Statist. 43, 627–635.CrossRefGoogle Scholar
Iglehart, D. L. (1974) Functional central limit theorems for random walks conditioned to stay positive. Ann. Prob. 2, 608–619.Google Scholar
Iglehart, D. L. (1975) Conditioned limit theorems for random walks. Stochastic Processes and Related Topics, Vol. 1, ed. Puri, M. Academic Press, New York.Google Scholar
Iglehart, D. L. and Whitt, W. (1971) The equivalence of functional central limit theorems for counting processes and associated partial sums. Ann. Math. Statist. 42, 1372–1378.Google Scholar
Kaigh, W. D. (1976) An invariance principle for random walk conditioned by a late return to zero. Ann. Prob. 4, 115–121.Google Scholar
Kao, P. (1978) Limiting diffusion for random walks with drift conditioned to stay positive. J. Appl. Prob. 15, 280–291.Google Scholar
Karlin, S. and Taylor, H. M. (1975) A First Course in Stochastic Processes, 2nd edn Academic Press, New York.Google Scholar
Kingman, J. F. C. (1964) A martingale inequality in the theory of queues. Proc. Camb. Phil. Soc. 59, 359–361.CrossRefGoogle Scholar
Kingman, J. F. C. (1965) The heavy traffic approximation in the theory of queues. Proc. Symp. on Congestion Theory, ed. Smith, W. L. and Wilkinson, W. E. University of North Carolina Press, Chapel Hill.Google Scholar
Kingman, J. F. C. (1970) Inequalities in the theory of queues. J. R. Statist. Soc. B 32, 102–110.Google Scholar
Lindvall, T. (1973) Weak convergence of probability measures and random functions in the function space D[0, ∞). J. Appl. Prob. 10, 109–121.Google Scholar
Miller, D. R. (1972) Existence of limits in regenerative processes. Ann. Math. Statist. 43, 1275–1282.Google Scholar
Nagaev, S. (1973) Local theorems and boundary problems in Rd, d ≧ 1 (in Russian). International Conference on Probability Theory and Mathematical Statistics, Vilnius.Google Scholar
Pyke, R. (1968) The weak convergence of the empirical process of random sample size. Proc. Camb. Phil. Soc. 64, 155–160.Google Scholar
Ross, S. M. (1974) Bounds on the delay distribution in GI/G/1 queues. J. Appl. Prob. 11, 417–421.CrossRefGoogle Scholar
Seal, H. L. (1969) Stochastic Theory of a Risk Business. Wiley, New York.Google Scholar
Seal, H. L. (1972) Risk theory and the single server queue. Mitteil. Verein. Schweiz. Versich. Math. 72, 171–178.Google Scholar
Sparre Andersen, E. (1957) On the collective theory of risk in the case of contagion betwen claims. Trans. XV Internat. Congr. Actuaries, New York 2, 219–227.Google Scholar
Stone, S. (1963) Weak convergence of stochastic processes defined on semi-infinite time intervals. Proc. Amer. Math. Soc. 14, 694–696.Google Scholar
Taylor, G. C. (1976) Use of differential and integral equations to bound ruin and queueing probabilities. Scand. Actuarial J. 197–208.Google Scholar
Thorin, O. (1971) Further remarks on the ruin problem in case the epochs of claims form a renewal process. Part I. Skand. Aktuarietidskr., 14–38.Google Scholar
Vervaat, W. (1972) Functional central limit theorems for processes with positive drift and their inverses. Z. Wahrscheinlichkeitsth. 23, 245–253.Google Scholar
Whitt, W. (1970) Weak convergence of probability measures on the function space D[0, ∞). Technical Report, Dept. of Administrative Sciences, Yale University.Google Scholar
Whitt, W. (1971) Weak convergence of first passage time processes. J. Appl. Prob. 8, 417–422.Google Scholar

Additional references added in proof

Asmussen, S. (1981b) Time-dependent approximations in some queueing systems with imbedded Markov chains related to random walks. Submitted for publication.Google Scholar
Bolthausen, E. (1976) On a functional central limit theorem for random walks conditioned to stay positive. Ann. Prob. 4, 480–485.CrossRefGoogle Scholar
Pakes, A. G. (1978) On the maximum and absorption time of left-continuous random walk. J. Appl. Prob. 15, 292–299.Google Scholar
Pechinkin, A. V. (1980) The limit distribution for a random walk with absorption. Theory Prob. Appl. 25, 580–583.CrossRefGoogle Scholar
Shimura, M. (1979) A limit theorem for conditional random walk. Tsukuba J. Math. 3, 81–101.Google Scholar
Siegmund, D. (1975) The time until ruin in collective risk theory. Mitteil. Verein Schweiz. Versich. Math. 75, 157–166.Google Scholar
Siegmund, D. (1979). Corrected diffusion approximations in certain random walk problems. Adv. Appl. Prob. 11, 701–719.CrossRefGoogle Scholar