Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Runnenburg, J.Th.
1985.
PROBABILITY THEORY AND ITS APPLICATIONS.
Statistica Neerlandica,
Vol. 39,
Issue. 2,
p.
181.
Ahlberg, Daniel
2015.
Asymptotics of First-Passage Percolation on One-Dimensional Graphs.
Advances in Applied Probability,
Vol. 47,
Issue. 01,
p.
182.
de Lima, Bernardo N. B.
Procacci, Aldo
and
Sanchis, Rémy
2015.
A Remark on Monotonicity in Bernoulli Bond Percolation.
Journal of Statistical Physics,
Vol. 160,
Issue. 5,
p.
1244.
Tzioufas, Achillefs
2017.
The randomly fluctuating hyperrectangles are spatially monotone.
Statistics & Probability Letters,
Vol. 130,
Issue. ,
p.
76.
de Lima, Bernardo N. B.
Rolla, Leonardo T.
and
Valesin, Daniel
2019.
Monotonicity and phase diagram for multirange percolation on oriented trees.
Random Structures & Algorithms,
Vol. 55,
Issue. 1,
p.
160.

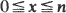 is always non-decreasing in
is always non-decreasing in 