Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T11:39:54.415Z Has data issue: false hasContentIssue false
  • English
  • Français

Determination of Boolean models by densities of mixed volumes

Part of: Inference from stochastic processes Stochastic processes General convexity Geometric probability and stochastic geometry

Published online by Cambridge University Press:  22 July 2019

Daniel Hug  and
Wolfgang Weil
Daniel Hug*
Affiliation:
Karlsruhe Institute of Technology (KIT)
Wolfgang Weil*
Affiliation:
Karlsruhe Institute of Technology (KIT)
*
*Postal address: Department of Mathematics, Karlsruhe Institute of Technology, 76128 Karlsruhe, Germany.
*Postal address: Department of Mathematics, Karlsruhe Institute of Technology, 76128 Karlsruhe, Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

In Weil (2001) formulae were proved for stationary Boolean models Z in ℝd with convex or polyconvex grains, which express the densities (specific mean values) of mixed volumes of Z in terms of related mean values of the underlying Poisson particle process X. These formulae were then used to show that in dimensions 2 and 3 the densities of mixed volumes of Z determine the intensity γ of X. For d = 4, a corresponding result was also stated, but the proof given was incomplete, since in the formula for the density of the Euler characteristic V̅0(Z) of Z a term 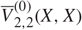$\overline V^{(0)}_{2,2}(X,X)$ was missing. This was pointed out in Goodey and Weil (2002), where it was also explained that a new decomposition result for mixed volumes and mixed translative functionals would be needed to complete the proof. Such a general decomposition result has recently been proved by Hug, Rataj, and Weil (2013), (2018) and is based on flag measures of the convex bodies involved. Here, we show that such flag representations not only lead to a correct derivation of the four-dimensional result, but even yield a corresponding uniqueness theorem in all dimensions. In the proof of the latter we make use of Alesker’s representation theorem for translation invariant valuations. We also discuss which shape information can be obtained in this way and comment on the situation in the nonstationary case.

Keywords

Stationary Boolean modelintensityspecific mean valuePoisson processmixed volumemixed functionaltranslative integral geometryflag measure

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry 52A22: Random convex sets and integral geometry
Secondary: 52A39: Mixed volumes and related topics 60G55: Point processes 62M30: Spatial processes
Type
Original Article
Information
Advances in Applied Probability , Volume 51 , Issue 1 , March 2019 , pp. 116 - 135
Copyright
© Applied Probability Trust 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alesker, S. (2001). Description of translation invariant valuations on convex sets with solution of P. McMullen’s conjecture. Geom. Funct. Anal. 11, 244–272.CrossRefGoogle Scholar
Goodey, P. and Weil, W. (2002). Representations of mixed measures with applications to Boolean models. Rend. Circ. Mat. Palermo (2) Suppl. 70, 325–346.Google Scholar
Hug, D. and Rataj, J. (2018). Mixed curvature measures of translative integral geometry. Geom. Dedicata 195, 101–120.CrossRefGoogle Scholar
Hug, D., Rataj, J. and Weil, W. (2013). A product integral representation of mixed volumes of two convex bodies. Adv. Geom. 13, 633–662.Google Scholar
Hug, D., Rataj, J. and Weil, W. (2018). Flag representations of mixed volumes and mixed functionals of convex bodies. J. Math. Anal. Appl. 460, 745–776.CrossRefGoogle Scholar
Hug, D., Türk, I. and Weil, W. (2013). Flag measures for convex bodies. In Asymptotic Geometric Analysis (Fields Inst. Commun. 68), eds Ludwig, M. et al., Springer, New York, pp. 145–187.CrossRefGoogle Scholar
Schneider, R. (2014). Convex Bodies: The Brunn-Minkowski Theory, 2nd expanded edn. Cambridge University Press.Google Scholar
Schneider, R. and Weil, W. (2008). Stochastic and Integral Geometry. Springer, Berlin.CrossRefGoogle Scholar
Schulte, J. and Weil, W. (2017). Valuations and Boolean models. In Tensor Valuations and Their Applications in Stochastic Geometry and Imaging (Lecture Notes Math. 2177), eds Vedel Jensen, E. B. and Kiderlen, M., Springer, Cham, pp. 301–338.Google Scholar
Weil, W. (2000). A uniqueness problem for non-stationary Boolean models. Rend. Circ. Mat. Palermo (2) Suppl. 65, 329–344.Google Scholar
Weil, W. (2001). Densities of mixed volumes for Boolean models. Adv. Appl. Prob. (SGSA) 33, 39–60.Google Scholar
Weil, W. (2017). Integral geometry of translation invariant functionals, II: The case of general convex bodies. Adv. in Appl. Math. 83, 145–171.CrossRefGoogle Scholar