Distributions of random variables involved in discrete censored δ-shock models

Abstract

Suppose that a system is affected by a sequence of random shocks that occur over certain time periods. In this paper we study the discrete censored 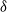$\delta$-shock model, 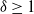$\delta \ge 1$, for which the system fails whenever no shock occurs within a 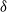$\delta$-length time period from the last shock, by supposing that the interarrival times between consecutive shocks are described by a first-order Markov chain (as well as under the binomial shock process, i.e., when the interarrival times between successive shocks have a geometric distribution). Using the Markov chain embedding technique introduced by Chadjiconstantinidis et al. (Adv. Appl. Prob. 32, 2000), we study the joint and marginal distributions of the system’s lifetime, the number of shocks, and the number of periods in which no shocks occur, up to the failure of the system. The joint and marginal probability generating functions of these random variables are obtained, and several recursions and exact formulae are given for the evaluation of their probability mass functions and moments. It is shown that the system’s lifetime follows a Markov geometric distribution of order 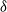$\delta$ (a geometric distribution of order 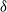$\delta$ under the binomial setup) and also that it follows a matrix-geometric distribution. Some reliability properties are also given under the binomial shock process, by showing that a shift of the system’s lifetime random variable follows a compound geometric distribution. Finally, we introduce a new mixed discrete censored 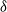$\delta$-shock model, for which the system fails when no shock occurs within a 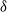$\delta$-length time period from the last shock, or the magnitude of the shock is larger than a given critical threshold 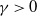$\gamma >0$. Similarly, for this mixed model, we study the joint and marginal distributions of the system’s lifetime, the number of shocks, and the number of periods in which no shocks occur, up to the failure of the system, under the binomial shock process.

1. Introduction

Shock models have been of great interest in reliability theory, operational research, and applied probability. Shock models are applied to study the lifetime of a system in the presence of a random environment. A classical shock model is based on a stochastic model that involves interarrival times between successive shocks, magnitudes of shocks, and a particular rule which defines the failure criteria of the system. Numerous shock models have been defined and studied in the literature from different perspectives. The extreme and cumulative shock models are the basic models that have been extensively studied in the literature. In the extreme (cumulative) shock model, a system that is subject to shocks of random magnitudes at random times breaks down when an individual shock magnitude (the cumulative shock magnitude) exceeds some given threshold (see, for example, Cha and Finkelstein [10], Cirillo and Hüsler [13], Gut and Hüsler [25], Gut [23], and Shanthikumar and Sumita [43]). Many researchers have defined and investigated modifications and generalizations of these two traditional models, such as $\delta$ -shock models, run shock models, and mixed shock models. In the $\delta$ -shock model, the system fails whenever the time between two consecutive shocks falls below a fixed threshold $\delta$ (Li [27], Wang and Zang [46], Xu and Li [50], Li and Kong [28], Li and Zhao [29], Li et al. [30], Bai and Xiao [4], Eryilmaz and Bayramoglou [19]), whereas under the setup of the run shock model, the system fails when the magnitudes of a specified number of consecutive shocks exceed a given threshold $\gamma $ (Sumita and Shanthikumar [45], Gut [23], Mallor and Omey [36]). The above-mentioned papers study the lifetime behavior of the system when the shocks occur according to a Poisson process, i.e. the interarrival times between shocks are exponentially distributed. Eryilmaz [18] studied the $\delta$ -shock model when the shock arrival process is described by a Pólya process which has dependent interarrival times. Eryilmaz [14] introduced and studied the lifetime of a generalized $\delta$ -shock model, under which the system breaks down whenever the lengths of $k\ge 1$ consecutive interarrival times are less than a given threshold $\delta$ and the shocks occur according to a Poisson process. Under the $\delta$ -shock model, the failure time of the system depends only on the interarrival times between shocks. In the mixed shock models, two or more types of classical shocks affect the behavior of the system. One is based on the interarrival time between successive shocks, and the other is based on the magnitude of a single shock and/or the cumulative shock magnitude. For example, in the mixed $\delta$ -shock model and the extreme shock model, the system fails if the interarrival time between two consecutive shocks is less than a given positive value, say $\delta$ , or the magnitude of a single shock is more than a positive value, say $\gamma$ (Wang and Zang [47], Rafiee et al. [42], Parvardeh and Balakrishnan [40], Lorvand et al. [31–33]).

Ma and Li [35] introduced a new shock model, called the censored $\delta$ -shock model, in which the system fails whenever no shock occurs within a $\delta$ -length time period from the last shock. Ma and Li [35] applied this model to describe customer relationships in trading management. A customer’s lifetime can be treated as the sum of $\delta$ and all previous trade times. When the interval between two successive trades between the customer and the trading company exceeds a threshold $\delta$ , a subsequent trade from this customer can be regarded as a trade from a new customer. The censored $\delta$ -shock model has many other applications in several fields, such as engineering, medicine, and management; for more examples, see Bai et al. [3] and Bian et al. [6].

Ma and Li [35] investigated the lifetime distribution of the censored $\delta$ -shock model and some related properties assuming that the system is subjected to external shocks under the classical assumption that shocks arrive according to a Poisson process, i.e., when the times between arrivals of successive shocks have a common exponential distribution. Eryilmaz and Bayramoglu [19] studied the lifetime distribution of the censored $\delta$ -shock model assuming that the external shocks arrive according to a renewal process such that the interarrival times of shocks follow the uniform distribution. Bai et al. [3] examined the parameter estimation of the censored $\delta$ -shock model.

In the above setups, the studies focused on the evaluation of the system’s lifetime in a continuous setup, in the sense that shocks arrive according to a renewal process and the times between successive shocks have a continuous probability distribution. However, in some cases the shocks may occur over discrete periods. In many real-life problems, the sojourn time in a state may be expressed by a number of specific cycles, e.g., the number of hours, days, or weeks that have passed, which can be modeled by a random variable having a discrete probability distribution. On the other hand, discrete-time shock models can be used to approximate continuous-time shock models. Several studies have been made of discrete shock models, i.e., when the interarrival times of shocks have a discrete probability distribution. See, for example, Eryilmaz [14–17], Gut [24], Aven and Gaarder [2], Nanda [39], Nair [38], Eryilmaz and Tekin [21], Eryilmaz and Kan [20], Chadjiconstantinidis and Eryilmaz [12], Lorvand et al. [32, 33], Lorvand and Nematollahi [31], and the references therein.

Under the discrete setup, Bian et al. [6] studied the lifetime of the censored $\delta$ -shock model when the times between successive shocks have a common geometric distribution and obtained the probability mass function (PMF), the probability generating function (PGF), the mean and the variance of system’s lifetime, and the joint PMF of the system’s lifetime and the number of shocks until the failure of the system. Also, they obtained the PMF of the system’s lifetime when the shocks arrive according to a specific first-order discrete-time Markov chain, in the sense that the initial probability of shock process at time zero has a special distribution.

Ma et al. [34] generalized the model of Bian et al. [6] by considering shocks that arrive according to a first-order discrete-time Markov chain with an arbitrary initial probability of shock at time zero and obtained the PMF, the mean of the system’s lifetime, and the joint PMF of the system’s lifetime and the number of shocks until the failure of the system.

In this paper, we examine the joint and marginal distributions involved in a discrete censored $\delta$ -shock model, i.e., the system’s lifetime, the number of shocks until the failure of the system, and the number of periods in which no shocks occur, up to the failure of the system.

Consider a system which is subject to external shocks, and let $X_i$ denote the interarrival time between the $(i-1)$ th and ith shocks. The shocks arrive according to a discrete renewal process at times $n=0$ , 1, $\cdots $ . It is assumed that $\{X_1$ , $X_2$ , $\cdots \}$ constitute a sequence of nonnegative discrete independent and identically distributed (i.i.d.) random variables.

We recall that under the censored $\delta$ -shock model, the system fails when no shock occurs within a $\delta$ -length time period from the last shock. In this model, the lifetime $T_{\delta }$ of the system is defined by the shifted compound random variable (or random sum)

(1) \begin{equation} T_{\delta }=\sum^{M_{\delta }}_{i=0}{X_i+\delta },\end{equation}

where

(2) \begin{equation} \left\{M_{\delta }=n\right\}=\{X_1\le \delta, \cdots, X_n\le \delta, X_{n+1}>\delta \}, \qquad n=0, 1, 2, \cdots,\end{equation}

for a prespecified level $\delta \ge 1$ with $X_0\equiv 0$ . Therefore, the random variable $M_{\delta }$ represents the number of shocks occurring until the failure of the system.

Usually, in the study of the random sums, it is assumed that the random variables $X_i$ and $M_{\delta }$ are independent. However, in the random sum (1) these random variables are dependent, and hence it is mathematically intractable to use this representation to find the distribution of $T_{\delta }$ . To overcome this difficulty, we define the following sequence of i.i.d. binary random variables:

(3) \begin{equation} I_n=\left\{ \begin{array}{l@{\quad}l} 1&\text{if a shock occurs in period} {n}, \\ \\[-8pt] 0&\text{otherwise}, \end{array} \right. \qquad n=1, 2, \cdots.\end{equation}

Let us denote by S (success) the event $\{I_n=1\}$ and by F (failure) the event $\{I_n=0\}$ . Then the problem of evaluating the distribution of $T_{\delta }$ can be equivalently transformed to a waiting problem. The lifetime $T_{\delta }$ is distributed as the waiting time random variable, say $W_{\delta }$ , for the first occurrence of the pattern ‘no success occurs within a $\delta$ -length time period from the last success’. That is, $W_{\delta }$ (and hence $T_{\delta }$ ) is the waiting time until a sequence of $\delta$ consecutive failures (or a failure run of length $\delta$ ) is observed for the first time. Under this framework, it is noteworthy that the random variable $T_{\delta }$ and/or $W_{\delta }$ can also defined using indicator variables, as

\[T_{\delta }=\mathrm{min}\mathrm{}\{n\ :\ I_{n-\delta +1}=I_{n-\delta +2}=\cdots =I_n=0\}.\]

Clearly, $W_{\delta }$ counts the number of binary trials required to observe for the first time the pattern

\[\underbrace{FF\cdots F}_{\delta }.\]

For example, if we consider the sequence of outcomes SFFSFSFFFSF, then $W_2=3$ , $W_3=9$ . Therefore, the study of the lifetime $T_{\delta }$ is equivalent to the study of the waiting time $W_{\delta }$ , and so in the rest of this section we shall use the random variable $T_{\delta }$ .

In the sequel, we introduce the discrete mixed censored $\delta$ -shock model. This model is obtained by combining the discrete censored $\delta$ -shock model defined above and the extreme shock model. Let $Z_i$ , $i\ge 1$ , be the magnitude of the ith shock; we assume that $\{Z_i$ , $i\ge 1\}$ is a sequence of i.i.d. random variables, independent of the interarrival times $\{X_i$ , $i\ge 1\}$ , having common df $G\left(x\right)=1-\overline{G}\left(x\right)=\mathrm{Pr}\mathrm{}(Z_i\le x)$ . Under this model, the system fails when no shock occurs within a $\delta$ -length time period from the last shock, or the magnitude of the shock is larger than a given critical threshold $\gamma >0$ .

In the mixed censored $\delta$ -shock model, the lifetime of the system is defined by

(4) \begin{equation} {\small T_{\delta,\gamma }=\left\{ \begin{array}{l} \sum^n_{i=0}{X_i}+\delta \qquad \text{if}\ X_1\le \delta \mathrm{,\ }Z_1\le \gamma \mathrm{,\ }\cdots \mathrm{,\ }X_n\le \delta \mathrm{,\ }Z_n\le \gamma \mathrm{,\ }X_{n+1}>\delta, \\ \\[-5pt] \sum^{n+1}_{i=0}{X_i}\qquad \text{if}\ X_1\le \delta \mathrm{,\ }Z_1\le \gamma \mathrm{,\ }\cdots \mathrm{,\ }X_n\le \delta \mathrm{,\ }Z_n\le \gamma \mathrm{,\ }X_{n+1}\le \delta \mathrm{,\ }Z_{n+1}>\gamma, \end{array} \right.}\end{equation}

with $X_0\equiv 0$ . It should be noted that when $\gamma \to \infty $ , the mixed censored $\delta$ -shock model is reduced to the censored $\delta$ -shock model.

Now let us consider some processes according to which the shocks may occur:

• The binomial process or the i.i.d. model: We assume that the external shocks arrive according to a binomial process at times $n=1$ , 2, $\cdots $ . That is, a shock occurs with probability p and does not occur with probability $q=1-p$ in any period of time $n=1$ , 2, $\cdots $ . Then all the random variables $X_0$ , $X_1$ , $X_2$ , $\cdots $ are i.i.d. following the zero-truncated geometric distribution with PMF ${\mathrm{Pr} \left(X_i=x\right)=pq^{x-1}\ }$ , $x=1$ , 2, $\cdots $ . In this case, the random variables $I_n$ , $n=1$ , 2, $\cdots $ , defined by (3) are i.i.d. and follow the Bernoulli distribution with parameter p. Note that for $\delta =1$ , the random variable $T_{\delta }$ follows the usual geometric distribution, and hence it is only interesting to assume $\delta >1$ .

• The Markov process: We assume that the shocks occur according to a two-state Markov chain. In this case, the random variables $I_n$ , $n=1$ , 2, $\cdots $ , defined by (3) are a time-homogeneous two-state Markov chain with transition probabilities

  \[p_{ij}={\mathrm{Pr} (I_n={j}/{I_{n-1}}=i)\ }, n\ge 2, i, j\in \{0, 1\} (p_{i0}+\mathrm{\ }p_{i1}=1)\]
  and initial probabilities $p_0={\mathrm{Pr} (I_1=0)}$ , $p_1={\mathrm{Pr} (I_1=1)\ }$ (with $p_0+p_1=1$ ). Under this setup, the distributions of the interarrival times between successive shocks have PMF given by
  (5) \begin{equation} \mathrm{Pr} \left(X_i=x\right)=\left\{ \begin{array}{l@{\quad}l} p_{11},& x=1, \\ \\[-6pt] p_{10}p^{x-2}_{00}p_{01},& x\ge 2, \end{array} \right. \ \text{for any} \ i\ge 1. \end{equation}
  Of course, for $p_1=p_{01}=p_{11}=p$ , $p_0=p_{00}=p_{10}=q=1-p$ , this model is reduced to the i.i.d. model.

In this paper we study the joint and marginal distributions of the random variables that are involved in a discrete censored $\delta$ -shock model, namely the random variables $T_{\delta }$ , $M_{\delta }$ , and $N_{\delta }$ , where $N_{\delta }$ represents the number of periods in which no shocks occur, until the failure of the system. As stated previously, the problem of evaluating the distribution of $T_{\delta }$ can be equivalently transformed to a waiting problem on binary sequences. Hence, in Section 2 we give some preliminary results for our subsequent analysis. In Subsection 2.1 we discuss the Markov chain imbedding technique developed by Chadjiconstantinidis et al. [11] for the study of the joint distribution of the number of successes, the number of failures, and the number of occurrences of any pattern in a sequence of binary trials, which we shall use in Section 3 in order to obtain the joint PGFs of the random variables $M_{\delta }$ (which equivalently corresponds to the number of successes), $N_{\delta }$ (which corresponds to the number of periods in which no shocks occur, until the failure of the system), and $T_{\delta }$ (which corresponds to the pattern ‘no success occurs within a $\delta$ -length time period from the last success’) under the Markov shock process and (as a special case) under the binomial shock process. The distribution of the system’s lifetime $T_{\delta }$ is discussed in detail in Section 4. The PMF is obtained, and it is shown that under the Markov shock process, $T_{\delta }$ follows a Markov geometric distribution of order $\delta$ ; hence, under the binomial shock process, it follows a geometric distribution of order $\delta$ . Several recursions for the evaluation of the PMF, the survival function, and the moments of $T_{\delta }$ are given. An exact matrix-form relationship for the PMF and the survival function of $T_{\delta }$ is also given, by showing that the distribution of $T_{\delta }$ has a matrix-geometric distribution. Also it is shown that under the binomial shock process, the random variable $T_{\delta }-\delta$ has a compound geometric distribution; using this, we get an upper bound for the survival function of $T_{\delta }$ , and we show that the distribution of $T_{\delta }-\delta$ belongs to some reliability classes. In Section 5 we examine the marginal distributions of the random variables $M_{\delta }$ and $N_{\delta }$ . Finally, in Section 6 we study the mixed censored $\delta$ -shock model under the binomial shock process, and we get results corresponding to those given in Section 4.

2. Some preliminary results

2.1. A Markov chain imbedding technique

As stated previously, the main tool for deriving our main result, given by Theorem 3.1 below, is the Markov chain embedding technique developed by Chadjiconstantinidis et al. [11], and thus we deem it necessary to outline briefly this technique.

Let $Z_1$ , $Z_2$ , $\cdots $ be a sequence of binary outcomes (trials) taking on the values 1 (success, S) or 0 (failure, F), and denote by $\mathcal{P}$ any pattern, i.e. a string (or a collection of strings) of outcomes with a prespecified composition. The number of successes and failures among $Z_1$ , $Z_2$ , $\cdots $ , $Z_n$ (where n is a fixed integer) will be denoted by $S_n$ and $F_n$ respectively. Let $W_r$ denotes the waiting time till the rth appearance of the pattern $\mathcal{P}$ . We are interested in the joint distribution of the waiting time $W_1$ till the first occurrence of $\mathcal{P}$ , and in the number of successes $S_{W_1}$ and the number of failures $F_{W_1}$ at that point (i.e., the number of successes and failures in the sequence $Z_1$ , $Z_2$ , $\cdots$ , $Z_{W_1}$ ). The main assumption made here is that the number, say $V_n$ , of occurrences of $\mathcal{P}$ in n trials is a Markov chain imbeddable variable of binomial type, which is defined below.

According to Koutras and Alexandrou [26], an integer-valued random variable $V_n$ (where n is a nonnegative integer) defined on $\{0$ , 1, $\cdots,$ $l_n\}$ , is called a Markov chain imbeddable variable if the following hold:

1. (i) There exists a Markov chain $\{Y_t\,{:}\,t\ge 0\}$ defined on a state space $\Omega$ .

2. (ii) There exists a partition $\{{\mathcal{C}}_x,\ x=0$ , 1, $\cdots \}$ on $\Omega$ .

3. (iii) For every $x\in \{0$ , 1 $\cdots,$ $l_n\}$ , the event $\{V_n=x\}$ is equivalent to the event $\{Y_n\in {\mathcal{C}}_x\}$ , i.e.

   \[{\mathrm{Pr} \left(V_n=x\right)={\mathrm{Pr} (Y_n\in {\mathcal{C}}_x)}}.\]

Without loss of generality, we assume that the sets (state subspaces) ${\mathcal{C}}_x$ of the partition $\{{\mathcal{C}}_x,\ x=0$ , 1, $\cdots \}$ have the same cardinality $s=\left|{\mathcal{C}}_x\right|$ for any $x\ge 0$ ; more specifically, ${\mathcal{C}}_x=\left\{c_{x,0},\ c_{x,1},\ \cdots,\ c_{x,\ s-1}\right\}$ . Then the nonnegative random variable $V_n$ is called a Markov chain imbeddable variable of binomial type (MVB) if

1. (a) $V_n$ is a Markov chain imbeddable variable, and

2. (b) ${\mathrm{Pr} (Y_t\in c_{y,j}\left|Y_{t-1}\in c_{x,i})=0\right.}$ for all $y\neq x, x+1$ and $t\ge 0$ .

As in Chadjiconstantinidis et al. [11], for the Markov chain $\{Y_t\,{:}\,t\ge 0\}$ we introduce the four $s\times s$ transition probability matrices

\[{\boldsymbol{{A}}}_{t,j}\left(x,y\right)=\left[\mathrm{Pr}\left(Y_t=c_{x,i^{\prime}},\ S_t=y+j\left|Y_{t-1}=c_{xi}\right.,\ S_{t-1}=y\right)\right], \qquad j=0, 1,\]

\[{\boldsymbol{{B}}}_{t,j}\left(x,y\right)=\left[\mathrm{Pr}\left(Y_t=c_{x+1,i^{\prime}},\ S_t=y+j\left|Y_{t-1}=c_{xi}\right.,\ S_{t-1}=y\right)\right], \qquad j=0, 1,\]

and define the $1\times s$ vector $\boldsymbol{{a}}\left(\rho \right)$ by

(6) \begin{equation} \boldsymbol{{a}}\left(\rho \right)={\boldsymbol{{f}}}_1\left(0,0\right)+\rho {\boldsymbol{{f}}}_1(0,1),\end{equation}

where the $1\times s$ probability vector ${\boldsymbol{{f}}}_1\left(x,y\right)$ is defined by

(7) \begin{equation} {\boldsymbol{{f}}}_1\left(x,y\right)=(\mathrm{Pr}(Y_1=c_{x,0},\ Z_1=y), \cdots, \mathrm{Pr}(Y_1=c_{x,s-1},\ Z_1=y)).\end{equation}

By ${\boldsymbol{{e}}}_i$ , $i=1$ , 2, $\cdots $ , s, we denote the unit vectors of ${\mathbb{R}}^s$ , and the symbol ‘T’ denotes the transpose of a matrix and/or vector.

For homogeneous MVBs (which is our case), i.e., where the matrices ${\boldsymbol{{A}}}_{t,j}\left(x,y\right)$ , ${\boldsymbol{{B}}}_{t,j}\left(x,y\right)$ do not depend on t, x, y, we set ${\boldsymbol{{A}}}_{t,j}\left(x,y\right)={\boldsymbol{{A}}}_j$ , ${\boldsymbol{{B}}}_{t,j}\left(x,y\right)={\boldsymbol{{B}}}_j$ , $j=0$ , 1, and let

(8) \begin{equation} {\beta}_{i,j}={\boldsymbol{{e}}}_i{\boldsymbol{{B}}}_j{\textbf{1}}^T_s, \qquad j=0,1 \ \text{and} \ i=1,2,\cdots,s,\end{equation}

where ${\textbf{1}}_s$ denotes the $1\times s$ unit vector. Also, let ${\boldsymbol{{I}}}_s$ be the $s\times s$ identity matrix.

In the following proposition we show how to obtain the joint PGF of the random vector $(F_{W_1}$ , $S_{W_1}$ , $W_1)$ in terms of the matrices ${\boldsymbol{{A}}}_j$ and ${\boldsymbol{{B}}}_j$ , $j=0$ , 1.

Proposition 2.1. If ${\boldsymbol{{A}}}_{t,j}\left(x,y\right)={\boldsymbol{{A}}}_j$ , ${\boldsymbol{{B}}}_{t,j}\left(x,y\right)={\boldsymbol{{B}}}_j$ , $j=0$ , 1, for all x, y and $t\ge 1$ , then the joint PGF $Hz,u,t)=\mathbb{E}[z^{F_{W_1}}u^{S_{W_1}}t^{W_1}]$ of the random vector $(F_{W_1}$ , $S_{W_1}$ , $W_1)$ is given by

\[H\left(z,u,t\right)=zt^2\boldsymbol{{a}}\left({u}/{z}\right)\sum^s_{i=1}{({\beta }_{i,0}z+{\beta }_{i,1}u)\left\{{\boldsymbol{{I}}}_s-t[zA_0+{\left.uA_1]\right\}}^{-1}\right.}{\boldsymbol{{e}}}^T_i,\]

where $\boldsymbol{{a}}\left({u}/{z}\right)$ and ${\beta }_{i,j}$ are given by (6) and (8) respectively.

Proof. Define the generating function

\[H\left(z,u,t;\ w\right)=\sum^{\infty }_{r=1}{\mathbb{E}[z^{F_{W_r}}u^{S_{W_r}}t^{W_r}]w^r}.\]

Then, from the relation (4.8) in Chadjiconstantinidis et al. [11], we have

\begin{align} H\left(z,u,t;\ w\right)&=zwt^2\boldsymbol{{a}}\left({u}/{z}\right)\sum^s_{i=1}{({\beta }_{i,0}z+{\beta }_{i,1}u)} \nonumber \\[3pt] &\quad \times {\left\{{\boldsymbol{{I}}}_s-t\left[z{\boldsymbol{{A}}}_0+u{\boldsymbol{{A}}}_1+w(z{\boldsymbol{{B}}}_0+u{\boldsymbol{{B}}}_1)\right]\right\}}^{-1}{\boldsymbol{{e}}}^T_i, \nonumber \end{align}

where $\boldsymbol{{a}}\left({u}/{z}\right)$ and ${\beta }_{i,j}$ are given by (6) and (8) respectively. Since

\[H\left(z,u,t\right)=\frac{\partial }{\partial w}\ H\left(z,u,t;\ w\right)\left|w=0\right.\!,\]

the result follows immediately from the above expression for $H\left(z,u,t;\ w\right)$ .

2.2. On discrete compound geometric and geometric distributions of order $\boldsymbol{{k}}$

Another notion of interest in this paper is the discrete compound geometric distribution. A random variable N following the geometric distribution with PMF ${\mathrm{Pr} \left(N=n\right)\ }=\theta {(1-\theta )}^n$ , $n=0$ , 1, 2, $\cdots $ , $0<\theta <1$ , will be denoted by $N\sim Geo(\theta )$ .

Let us consider the random sum H defined by

\[H=\left\{ \begin{array}{l@{\quad}l} 0,& N=0, \\ \\[-8pt] Y_1+Y_2+\cdots +Y_N,& N\ge 1, \end{array}\right.\]

where $\{Y_i,\ i\ge 1\}$ is a sequence of i.i.d. random variables which are also independent of N. If $Y_i,\ i\ge 1$ , are discrete random variables with common PMF $f_{Y_1}\left(y\right)=Pr(Y_1=y)$ and $N\sim Geo(\theta )$ , then H is said to follow the discrete compound geometric distribution, abbreviated as $H\sim D$ - $CGeo(\theta )$ , $f_{Y_1})$ . It is well known (see, e.g., Willmot and Lin [49]) that the PGF $P_H\left(z\right)=\mathbb{E}[z^H]$ of H is given by

(9) \begin{equation} P_H\left(z\right)=\frac{\theta }{1-(1-\theta )P_{Y_1}(z)},\end{equation}

where $P_{Y_1}\left(z\right)=\mathbb{E}[z^{Y_1}]$ is the PGF of $Y_1$ , and the PMF $f_H\left(x\right)=\mathrm{Pr}\mathrm{}(H=x)$ and the survival function ${\overline{F}}_H\left(x\right)=\mathrm{Pr}\mathrm{}(H>x)$ satisfy the discrete defective renewal equations

(10) \begin{equation} f_H\left(x\right)=(1-\theta )\sum^x_{i=1}{f_{Y_1}\left(i\right)f_H\left(x-i\right)}, \qquad x=1, 2, \cdots\end{equation}

with initial condition $f_H\left(0\right)=\theta $ , and

(11) \begin{equation} {\overline{F}}_H\left(x\right)=(1-\theta )\sum^x_{i=1}{f_{Y_1}\left(i\right){\overline{F}}_H\left(x-i\right)+(1-\theta ){\overline{F}}_Y\left(x\right)}, \qquad x=0, 1, \cdots\end{equation}

The mean and the variance of H are given by

(12) \begin{equation} \mathbb{E}\left[H\right]=\frac{1-\theta }{\theta }\mathbb{E}[Y_1] \ \ \text{and} \ \ Var\left[H\right]=\frac{1-\theta }{\theta }Var\left[Y_1\right]+\frac{1-\theta }{{\theta }^2}\mathbb{E}^2[Y_1]. \end{equation}

A generalization of the geometric distribution is the so-called geometric distribution of order k (Philippou et al. [41]) introduced by Feller [22], as well as the Markov geometric distribution of order k (Balakrishnan and Koutras [5]).

Let $Z_1$ , $Z_2$ , $\cdots $ be a sequence of independent binary (Bernoulli) trials each resulting in one of two possible outcomes, say A and $\overline{A}$ , with ${\mathrm{Pr} \left(A\right)\ }$ $=1-{\mathrm{Pr} \left(\overline{A}\right)\ }=\theta$ ; that is, ${\mathrm{Pr} \left(Z_i=1\right\}\ }={\mathrm{Pr} \left(A\right)\ }=\theta $ , ${\mathrm{Pr} \left(Z_i=0\right\}\ }={\mathrm{Pr} \left(\overline{A}\right)\ }=1-\theta $ , for every $i=1, 2, \cdots $ . Let the random variable $U_k$ be the waiting time in the sequence of independent experiments until the first occurrence of k consecutive As, i.e., until the first occurrence of the pattern $\underbrace{AA\cdots A}_{k\ \text{times}}$ . Then $U_k$ is said to have the geometric distribution of order k with PGF $P_{U_k}\left(z\right)=\mathbb{E}[z^{U_k}]$ given by Aki et al. [1],

(13) \begin{equation} P_{U_k}\left(z\right)=\frac{(1-\theta z){(\theta z)}^k}{1-z+(1-\theta ){\theta }^kz^{k+1}},\end{equation}

and will be denoted by $U_k\sim {Geo}_k(\theta )$ . Obviously, if the random variable ${\overline{U}}_k$ denotes the waiting time in the sequence of independent experiments until the first occurrence of k consecutive $\overline{A}$ s, then ${\overline{U}}_k\sim {Geo}_k(1-\theta )$ . Note that for $k=1$ we have ${Geo}_1\left(\theta \right)=Geo(\theta )$ (and hence $U_1=N$ ); i.e., the geometric distribution of order 1 is reduced to the usual geometric distribution.

Suppose now that the binary sequence $Z_1$ , $Z_2$ , $\cdots $ is a time-homogeneous two-state Markov chain with transition probability matrix

\[\left[ \begin{array}{c@{\quad}c} {\theta }_{00} & {\theta }_{01} \\ \\[-8pt] {\theta }_{10} & {\vartheta }_{11} \end{array}\right],\]

that is, with ${\theta }_{ij}=\mathrm{Pr}\mathrm{}(Z_t=j\left|Z_{t-1}=i)\right.$ , $t\ge 2$ , $0\le i, j\le 1$ , and initial probabilities ${\theta }_j=\mathrm{Pr}\mathrm{}(Z_1=j)$ , $j=0$ , 1. The distribution of the waiting time $U_k$ for the first occurrence of a run $\underbrace{AA\cdots A}_{k\ \text{times}}$ in the sequence $Z_1$ , $Z_2$ , $\cdots $ will be called the Markov geometric distribution of order k (Balakrishnan and Koutras [5]), abbreviated as $U_k\sim M{Geo}_k({\theta }_1;\ {\theta }_{00},\ {\theta }_{11})$ . The PGF of $U_k$ is given by the relation (2.45) in Balakrishnan and Koutras [5]:

(14) \begin{equation} P_{U_k}\left(z\right)=\frac{{\theta }^{k-1}_{11}\{{\theta }_1+\left({\theta }_0{\theta }_{01}-{\theta }_1{\theta }_{00}\right)z\}z^k}{1-{\theta }_{00}z-{\theta }_{01}{\theta }_{10}z^2\sum^{k-2}_{i=0}{{({\theta }_{11}z)}^i}} .\end{equation}

Manifestly, if we set ${\theta }_1={\theta }_{01}={\theta }_{11}=\theta $ and ${\theta }_0={\theta }_{10}={\theta }_{00}=1-\theta $ , we get the ${Geo}_k(\theta )$ distribution, i.e., $M{Geo}_k\left(\theta ;\ 1-\theta,\ \theta \right)={Geo}_k(\theta )$ .

3. Some results on joint distributions

The main result of this section is given in the next theorem, where we give the joint PGF of the lifetime $T_{\delta }$ and the random variables involved, $N_{\delta }$ and $M_{\delta }$ . We recall that the random variable $M_{\delta }$ defined by (2) represents the number of shocks that occur before the failure of the system, whereas the random variable $N_{\delta }$ represents the number of periods in which no shocks occur, up to the failure of the system. Hence, according to the notation of the previous section, we have $M_{\delta }=S_{T_{\delta }}$ and $N_{\delta }=F_{T_{\delta }}$ , where S (success) denotes the event $\{I_n=1\}$ (the occurrence of a shock in the nth period), and F (failure) denotes the event $\{I_n=0\}$ (the non-occurrence of a shock in the nth period).

Theorem 3.1. For the Markov shock process, the joint PGF

$$G^{\left(012\right)}_{\delta }\left(z,u,t\right)=\mathbb{E}\left[z^{N_{\delta }}u^{M_{\delta }}t^{T_{\delta }}\right]$$

of the random vector $(N_{\delta }, M_{\delta }, T_{\delta })$ is given by

(15) \begin{equation} G^{\left(012\right)}_{\delta }\left(z,u,t\right)=\frac{[p_0+\left(p_1p_{10}-p_0p_{11}\right)zt]p^{\delta -1}_{00}{(zt)}^{\delta }}{1-utp_{11}-zut^2p_{01}p_{10}\sum^{\delta -2}_{i=0}{{(p_{00}zt)}^i}} . \end{equation}

Proof. Let $W_{\delta, 1}$ be the waiting time until the first occurrence of the pattern $\mathcal{P}=\{\underbrace{FF\cdots F}_{\delta \ \text{times}}\}$ in the sequence of the two-state Markov chain $I_1$ , $I_2$ , $\cdots $ described in Section 1. Then it holds that $T_{\delta }\triangleq W_{\delta,}\triangleq W_{\delta, 1}$ , $N_{\delta }\triangleq F_{W_{\delta,1}}$ , $M_{\delta }\triangleq S_{W_{\delta,1}}$ , and $G^{\left(012\right)}_{\delta }\left(z,u,t\right)=H\left(z,u,t\right)$ .

In order to view the random variable $T_{\delta }$ as an MVB, we define

\[{\mathcal{C}}_x=\{c_{x,0},\ c_{x,1},\ \cdots,\ c_{x,\ \ k-1}\},\]

where $c_{x,i}=(x$ , i) for all $x=0$ , 1, $\cdots $ , $[{n}/{\delta }]$ ( $l_n=[{n}/{\delta }]$ , $s=\delta$ ), and we introduce a Markov chain $\{Y_t$ , $t\ge 0\}$ on $\mathrm{\Omega }={\cup }^{l_n}_{x=0}\mathcal{C}$ as follows: $Y_t=(x$ , i) if and only if, in the sequence of outcomes leading to the tth trial (say $FSFFS\cdots S\underbrace{FF\cdots F}_{m\ \text{times}}$ ), there exist x non-overlapping failure runs and m trailing failures with $m\equiv i \mod k$ .

Clearly, under this setup, the random variable $T_{\delta }$ becomes an MVB, and also the resulting Markov chain is homogeneous, with

\[{\boldsymbol{{A}}}_0=\left[ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} p_{11} & 0 & 0 & \cdots & 0 \\ \\[-8pt] p_{01} & 0 & 0 & \cdots & 0 \\ \\[-8pt] \vdots & \vdots & \vdots & \cdots & \vdots \\ \\[-8pt] p_{01} & 0 & 0 & \cdots & 0 \\ \\[-8pt] p_{01} & 0 & 0 & \cdots & 0 \end{array} \right] , \qquad {\boldsymbol{{A}}}_1=\left[ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0 & p_{10} & 0 & \cdots & 0 \\ \\[-8pt] 0 & 0 & p_{00} & \cdots & 0 \\ \\[-8pt] \vdots & \vdots & \vdots & \cdots & \vdots \\ \\[-8pt] 0 & 0 & 0 & \cdots & p_{00} \\ \\[-8pt] 0 & 0 & 0 & \cdots & 0 \end{array} \right],\]

${\boldsymbol{{B}}}_0={\boldsymbol{0}}_{\delta \times \delta }$ , and the only nonvanishing entry of ${\boldsymbol{{B}}}_1$ is the entry $(\delta$ , 1), where a $p_{00}$ is present.

Using (7), the $1\times \delta$ vector ${\boldsymbol{{f}}}_1\left(x,y\right)$ is given by

\[{\boldsymbol{{f}}}_1\left(x,y\right)=\left\{ \begin{array}{c@{\quad}l} {\boldsymbol{0}}_k,& x>0,\ \ y=0,\ 1,\ \\ \\[-8pt] p^y_0p^{1-y}_1{\boldsymbol{{e}}}_{y+1},& x=0,\ \ y=0,\ 1,\ \ \end{array} \right.\]

and hence from (6) it follows that the $1\times \delta$ vector $\boldsymbol{{a}}\left(\rho \right)$ is $\boldsymbol{{a}}\left(\rho \right)=(p_0$ , $p_1\rho $ , 0, $\cdots $ , 0), whereas from (8) we get

$${\beta }_{i,0}=0 \ \text{for all} \ i=1, 2, \cdots, \delta; \qquad {\beta }_{i,1}=\left\{ \begin{array}{c} 0,\ \ \ 1\le i\le \delta -1, \\ \\[-8pt] p_{00},\ \ \ \ \ \ \ \ \ \ \ i=\delta. \end{array} \right.$$

Hence, applying Proposition 2.1, it is straightforward to show that

\begin{align*}G^{\left(012\right)}_{\delta }\left(z,u,t\right)&=p_{00}zut^2\boldsymbol{{a}}\left({u}/{z}\right){\left\{{\boldsymbol{{I}}}_k-t[z{\boldsymbol{{A}}}_0+u{\boldsymbol{{A}}}_1]\right\}}^{-1}{\boldsymbol{{e}}}^T_{\delta }\\[3pt]&=p_{00}zut^2\left(p_0A_{\delta 1}+p_1\frac{u}{z}A_{\delta 2}\right),\end{align*}

where

\begin{align*} A_{\delta 1}&=\frac{utp_{10}{(utp_{00})}^{\delta -2}}{1-utp_{11}-zut^2p_{01}p_{10}\sum^{\delta -2}_{i=0}{{(p_{00}zt)}^i}}, \\ \\[-8pt] A_{\delta 2}&=\frac{(1-ztp_{11}){(utp_{00})}^{\delta -2}}{1-utp_{11}-zut^2p_{01}p_{10}\sum^{\delta -2}_{i=0}{{(p_{00}zt)}^i}}, \end{align*}

and thus (15) follows immediately.

By letting $p_0=q$ , $p_1=p$ , $p_{10}=p_{00}=q$ , $p_{01}=p_{11}=p$ , $0<p<1$ , $q=1-p$ , we obtain the following corollary directly from Theorem 3.1.

Corollary 3.1. For the binomial shock process, the joint PGF

$$G^{\left(012\right)}_{\delta }\left(z,u,t\right)=\mathbb{E}\left[z^{N_{\delta }}u^{M_{\delta }}t^{T_{\delta }}\right]$$

is given by

\[G^{\left(012\right)}_{\delta }\left(z,u,t\right)=\frac{{\left(qzt\right)}^{\delta }(1-qzt)}{1-qzt-put[1-{\left(qzt\right)}^{\delta }]} . \]

By letting $z=1$ in (15), we immediately obtain the following corollary giving the joint PGF of the number of shocks $M_{\delta }$ until the failure of the system and the lifetime $T_{\delta }$ of the system.

Corollary 3.2. (i) For the Markov shock process, the joint PGF

$$G^{\left(12\right)}_{\delta }\left(u,t\right)=\mathbb{E}\left[u^{M_{\delta }}t^{T_{\delta }}\right]$$

of the random vector $(M_{\delta },\ T_{\delta })$ is given by

\[G^{\left(12\right)}_{\delta }\left(u,t\right)=\frac{[p_0+\left(p_1p_{10}-p_0p_{11}\right)t]p^{\delta -1}_{00}t^{\delta }}{1-utp_{11}-ut^2p_{01}p_{10}\sum^{\delta -2}_{i=0}{{(p_{00}t)}^i}} . \]

(ii) For the binomial shock process, the joint PGF

$$G^{\left(12\right)}_{\delta }\left(u,t\right)=\mathbb{E}\left[u^{M_{\delta }}t^{T_{\delta }}\right]$$

of the random vector $(M_{\delta },\ T_{\delta })$ is given by

\[G^{\left(12\right)}_{\delta }\left(u,t\right)=\frac{(1-qt){(qt)}^{\delta }}{1-qt-put[1-{(qt)}^{\delta }]} .\]

Using Corollary 3.2, it is straightforward to obtain a recursive relationship for evaluating the joint PMF as well as the joint factorial moments of $(M_{\delta },\ T_{\delta })$ . For example, we get the following recursion for the joint PMF $f^{\left(12\right)}_{\delta }\left(m,n\right)=\mathrm{Pr}\mathrm{}(M_{\delta }=m,\ T_{\delta }=n)$ , m, $n\ge 0$ , under the binomial shock process

\[f^{\left(12\right)}_{\delta }\left(m,n\right)=qf^{\left(12\right)}_{\delta }\left(m,n-1\right)+pf^{\left(12\right)}_{\delta }\left(m-1,n-1\right)-pq^{\delta }f^{\left(12\right)}_{\delta }\left(m-1,n-\delta \right),\]

for any $m\ge 1$ , $n\ge \delta +2$ , with initial conditions

\begin{align*}f^{\left(12\right)}_{\delta }\left(0,n\right)&=0, \qquad n\ge 0 ; \\[3pt]f^{\left(12\right)}_{\delta }\left(1,n\right)&=0, \qquad 0\le n\le \delta -1; \\[3pt]f^{\left(12\right)}_{\delta }\left(1,\delta \right)&=q^{\delta}; \\[3pt]f^{\left(12\right)}_{\delta }\left(1,\delta +1\right)&=pq^{\delta }. \end{align*}

Also, by differentiating $G^{\left(12\right)}_{\delta }\left(u,t\right)$ with respect to u and t and then letting $u=t=1$ , we get

\[\mathbb{E}\left[M_{\delta }T_{\delta }\right]=\frac{1-(\delta +1)q^{\delta }}{q^{\delta }}+\frac{1-(\delta +1)pq^{\delta }}{{pq}^{\delta }}\mathbb{E}\left[M_{\delta }\right]+\frac{1-q^{\delta }}{q^{\delta }}\mathbb{E}\left[T_{\delta }\right],\]

and since ${\mathbb{E}[M}_{\delta }]=\frac{1-q^{\delta }}{q^{\delta }}$ (see Bian et al. [6]), the covariance of $M_{\delta }$ and $T_{\delta }$ is given by

\[Cov\left(M_{\delta },\ T_{\delta }\right)=\frac{1-(1+\delta p)q^{\delta }}{pq^{2\delta }}.\]

Since the numerator is a decreasing function in $0<q<1$ , it holds that $0<Cov\left(M_{\delta },\ T_{\delta }\right)<{1}/{pq^{2\delta }}$ .

Similarly, from Theorem 3.1 we directly obtain the following corollaries, from which we can easily obtain recursions for the corresponding PMF and the joint factorial moments. The results are immediate and therefore omitted.

Corollary 3.3. (i) For the Markov shock process, the joint PGF

$$G^{\left(02\right)}_{\delta }\left(z,t\right)=\mathbb{E}\left[z^{N_{\delta }}t^{T_{\delta }}\right]$$

of the random vector $(N_{\delta },\ T_{\delta })$ is given by

\[G^{\left(02\right)}_{\delta }\left(z,t\right)=\frac{[p_0+\left(p_1p_{10}-p_0p_{11}\right)zt]p^{\delta -1}_{00}(z{t)}^{\delta }}{1-tp_{11}-zt^2p_{01}p_{10}\sum^{\delta -2}_{i=0}{{(p_{00}zt)}^i}}. \]

(ii) For the binomial shock process, the joint PGF

$$G^{\left(02\right)}_{\delta }\left(z,t\right)=\mathbb{E}\left[z^{N_{\delta }}t^{T_{\delta }}\right]$$

of the random vector $(N_{\delta },\ T_{\delta })$ is given by

\[G^{\left(02\right)}_{\delta }\left(z,t\right)=\frac{(1-qzt){(qzt)}^{\delta }}{1-qzt-pt[1-{(qzt)}^{\delta }]} .\]

Corollary 3.4. (i) For the Markov shock process, the joint PGF

$$G^{\left(01\right)}_{\delta }\left(u,t\right)=\mathbb{E}\left[{z^{N_{\delta }}u}^{M_{\delta }}\right]$$

of the random vector $(N_{\delta },\ M_{\delta })$ is given by

\[G^{\left(01\right)}_{\delta }\left(z,u\right)=\frac{[p_0+\left(p_1p_{10}-p_0p_{11}\right)z]p^{\delta -1}_{00}z^{\delta }}{1-up_{11}-zup_{01}p_{10}\sum^{\delta -2}_{i=0}{{(p_{00}z)}^i}} .\]

(ii) For the binomial shock process, the joint PGF

$$G^{\left(01\right)}_{\delta }\left(u,t\right)=\mathbb{E}\left[{z^{N_{\delta }}u}^{M_{\delta }}\right]$$

of the random vector $(N_{\delta },\ M_{\delta })$ is given by

\[G^{\left(01\right)}_{\delta }\left(z,u\right)=\frac{(1-qz){(qz)}^{\delta }}{1-qz-pu[1-{(qz)}^{\delta }]} .\]

4. The distribution of the lifetime $\boldsymbol{T_\delta}$

In this section we shall study in some detail the distribution of the lifetime $T_{\delta }$ . By letting $z=u=1$ in (15), we immediately get the PGF of $T_{\delta }$ given in the next result.

Corollary 4.1. (i) For the Markov shock process, the PGF $G_{\delta }(t)=\mathbb{E}[t^{T_{\delta }}]$ of the lifetime $T_{\delta }$ is given by

(16) \begin{equation} G_{\delta }(t)=\frac{[p_0+\left(p_1p_{10}-p_0p_{11}\right)t]p^{\delta -1}_{00}t^{\delta }}{1-p_{11}t-p_{01}p_{10}t^2\sum^{\delta -2}_{i=0}{{(p_{00}t)}^i}}. \end{equation}

(ii) For the binomial shock process, the PGF $G_{\delta }(t)=\mathbb{E}[t^{T_{\delta }}]$ of the lifetime $T_{\delta }$ is given by

(17) \begin{equation} G_{\delta }\left(t\right)=\frac{{(1-qt)\left(qt\right)}^{\delta }}{1-t+pq^{\delta }t^{\delta +1}} . \end{equation}

Note that (17) was also proved by Bian et al. [6, Theorem 3.2] using a different approach.

Remark 4.1. (i) For the Markov shock process, from (14) and (16) it follows that the system’s lifetime $T_{\delta }$ follows a Markov geometric distribution of order $\delta$ , namely

\[T_{\delta }\sim M{Geo}_{\delta }(p_0;\ p_{11}, p_{00}).\]

(ii) For the binomial risk process, from (13) and (17) it follows that $T_{\delta }\sim {Geo}_{\delta }(q)$ .

Using Corollary 4.1 and the fact that $G_{\delta }\left(t\right)=\sum^{\infty }_{n=0}{f_{\delta }\left(n\right)t^n}$ , we can easily obtain a recursive relationship for evaluating the PMF $f_{\delta }\left(n\right)=\mathrm{Pr}\mathrm{}(T_{\delta }=n)$ , $n\ge 0$ .

Hence, for the Markov shock process, from (16) we directly obtain the recursion

\[f_{\delta }\left(n\right)=p_{11}f_{\delta }\left(n-1\right)+\sum^{\delta }_{i=2}{p_{01}p_{10}p^{i-2}_{00}f_{\delta }\left(n-i\right)}, n\ge \delta +2\]

with initial conditions

\begin{align*} f_{\delta }\left(n\right)&=0, \qquad 0\le n\le \delta -1 ; \\[3pt] f_{\delta }\left(\delta \right)&=p_0p^{\delta -1}_{00} ; \\[3pt] f_{\delta }\left(\delta +1\right)&=p_1p_{10}p^{\delta -1}_{00}. \end{align*}

By rewriting (16) equivalently as

\begin{align*}G_{\delta }\left(t\right)&=p_0p^{\delta -1}_{00}t^{\delta }+\left(p_1p_{10}-p_0p_{11}-p_0p_{00}\right)p^{\delta -1}_{00}t^{\delta +1}-(p_1p_{10}-p_0p_{11})p^{\delta }_{00}t^{\delta +2}\\[3pt]&\quad +\left(p_{00}+p_{11}\right)tG_{\delta }\left(t\right)+\left(p_{01}p_{10}-p_{00}p_{11}\right)t^2G_{\delta }\left(t\right)-p_{01}p_{10}{p^{\delta -1}_{00}t}^{\delta +1}G_{\delta }\left(t\right),\end{align*}

expanding both sides of this relation into a power series, and then picking up the coefficients of $t^n$ for all $n\ge 0$ in the resulting equation, we get a computationally more efficient recursive scheme which is given in the following result.

Corollary 4.2. (i) For the Markov shock process, the PMF $f_{\delta }\left(n\right)=\mathrm{Pr}\mathrm{}(T_{\delta }=n)$ satisfies the recursion

\[f_{\delta }\left(n\right)=\left(p_{00}+p_{11}\right)f_{\delta }\left(n-1\right)+\left(p_{01}p_{10}-p_{00}p_{11}\right)f_{\delta }\left(n-2\right)-p_{01}p_{10}p^{\delta -1}_{00}f_{\delta }\left(n-\delta -1\right)\]

for $n\ge \delta +3$ , with initial conditions

\[f_{\delta }\left(n\right)=\left\{ \begin{array}{l@{\quad}r} 0,& 0\le n\le \delta -1, \\ \\[-8pt] p_0p^{\delta -1}_{00},& n=\delta, \\ \\[-8pt] p_1p_{10}p^{\delta -1}_{00},& n=\delta +1, \\ \\[-8pt] \left(p_0p_{01}+p_1p_{11}\right)p_{10}p^{\delta -1}_{00},& n=\delta +2. \end{array} \right. \]

(ii) For the binomial shock process, the PMF $f_{\delta }\left(n\right)=\mathrm{Pr}\mathrm{}(T_{\delta }=n)$ satisfies the recursion

(18) \begin{equation} f_{\delta }\left(n\right)=f_{\delta }\left(n-1\right)-pq^{\delta }f_{\delta }\left(n-\delta -1\right), \qquad n\ge 2\delta +1, \end{equation}

with initial conditions

\[f_{\delta }\left(n\right)=\left\{ \begin{array}{l@{\quad}r} 0,& 0\le n\le \delta -1, \\ \\[-8pt] q^{\delta },& n=\delta, \\ \\[-8pt] pq^{\delta },& \delta +1\le n\le 2\delta. \end{array} \right. \]

For the binomial shock process, Bian et al. [6, Theorem 3.1] obtained an exact double summation formula for $f_{\delta }\left(n\right)$ . Using a result of Muselli [37] and interchanging the roles of p and q, we can establish a more attractive single summation formula for $f_{\delta }\left(n\right)$ , namely

\[f_{\delta }\left(n\right)=\sum^{\left[\frac{n+1}{\delta +1}\right]}_{i=1}{{(-1)}^{i-1}q^{i\delta }p^{i-1}}\left\{\left( \begin{array}{c} n-i\delta -1 \\ i-2 \end{array}\right)+p\left( \begin{array}{c} n-i\delta -1 \\ i-1 \end{array}\right)\right\}.\]

In the following, we represent the random variable $T_{\delta }$ as a matrix-geometric distribution. The PGF given by (13) is rational and has the form

\[G_{\delta }\left(t\right)=\frac{c_1t+\dots +c_mt^m}{1+d_1t+\dots +d_mt^m}\]

for some $m \geq 1$ and real constants $c_1,\dots,c_m$ and $d_1,\dots,d_m$ . A random variable with zero PMF at zero that has a PGF in this form is said to have a matrix-geometric distribution (see, e.g., Bladt and Nielsen [7]). In this case, the PMF and the survival function of the random variable $T_{\delta }$ can be represented respectively as

(19) \begin{equation} \mathrm{Pr}\left(T_{\delta }=n\right)=\boldsymbol{\pi }Q^{n-1}{\boldsymbol{{u}}}^{\prime}\end{equation}

and

(20) \begin{equation} \mathrm{Pr}\left(T_{\delta }>n\right)=\boldsymbol{\pi }Q^n{(I-Q)}^{-1}{\boldsymbol{{u}}}^{\prime},\end{equation}

where $\boldsymbol{\pi }=\left(1,0,\dots,0\right)\!,$

\[Q=\left[ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} -d_1 & 0 & 0 & &\cdots & 0 & 1 \\ \\[-9pt] -d_m & 0 & 0&& \cdots & 0 & 0 \\ \\[-9pt] -d_{m-1} & 1 & 0 &&\cdots & 0 & 0\\ \\[-9pt]-d_{m-2} & 0 & 1 && \cdots & 0 & 0\\ \\[-9pt] \vdots & \vdots & \vdots && \ddots & \vdots & \vdots \\ \\[-9pt] -d_2 & 0 & 0 && \cdots & 0 & 0 \end{array} \right],\qquad {\boldsymbol{{u}}}^{\prime}=\left[ \begin{array}{c} c_1 \\ \\[-9pt] c_m \\ \\[-9pt] c_{m-1} \\ \\[-9pt] c_{m-2} \\ \\[-9pt] \vdots \\ \\[-9pt] c_2 \end{array}\right].\]

Hence, from (16) we have $m=\delta +1$ and

\begin{align*}c_1=c_2=\cdots =c_{\delta -1}=0, \qquad c_{\delta }=p_0p^{\delta -1}_{00}, \qquad c_{\delta +1}=(p_1p_{10}-p_0p_{11})p^{\delta -1}_{00},\\[3pt]d_1=-p_{11}, \qquad d_i=-p_{01}p_{10}p^{i-2}_{00} \ \text{for} \ i=2, 3, \ldots, \delta, \qquad d_{\delta +1}=0.\end{align*}

Thus $f_{\delta }\left(n\right)$ and $\mathrm{Pr}\left(T_{\delta }>n\right)$ for the Markov shock process can be evaluated in matrix form through (18) and (19) respectively.

By direct differentiation of (16), it is easy to obtain the mean of $T_{\delta }$ (or the mean time to failure of the system, MTTF) for the Markov shock process as

\[\mathbb{E}\left[T_{\delta }\right]=\frac{p_{10}+p_{01}-p_0p^{\delta -1}_{00}+(p_0-p_{10})p^{\delta }_{00}}{p_{01}p_{10}p^{\delta -1}_{00}},\]

whereas for the binomial shock process, from (17) we find that the rth moment (about zero) of $T_{\delta }$ ,

\[{\mu }_r=\mathbb{E}\left[T^r_{\delta }\right]=\frac{d^r}{dt^r}G_{\delta }(e^t)\left|t=0\right.\!,\]

obeys the recursion

\[{\mu }_r=\sum^{r-1}_{i=0}{\left( \begin{array}{c} r \\ i \end{array} \right)\left\{\frac{1}{pq^{\delta }}-{(\delta +1)}^{r-i}\right\}}{\mu }_{r-i}+\frac{{\delta }^r-q{(\delta +1)}^r}{p}, \qquad r\ge 1.\]

Therefore, we get that the MTTF and the variance of $T_{\delta }$ for the binomial shock process are

(21) \begin{equation} \mathbb{E}\left[T_{\delta }\right]=\frac{1-q^{\delta }}{pq^{\delta }}, \ \ \ Var\left[T_{\delta }\right]=\frac{1-\left(2\delta +1\right)pq^{\delta }-q^{2\delta +1}}{p^2q^{2\delta }},\end{equation}

which are also given in Corollaries 3.1 and 3.2, respectively, of Bian et al. [6].

Now let us consider the problem of approximating the distribution of the lifetime $T_{\delta }$ . By $a(x)\sim b(x)$ we indicate that ${\mathop{\mathrm{lim}}_{x\to \infty } \left({a(x)}/{b(x)}\right)=1}$ . Thus, we have the following result.

Theorem 4.1. For the Markov shock process, it holds that

$$f_{\delta }\left(n\right)\sim \frac{(1-p_{00}x)(a_0+a_1x+a_2x^2+a_3x^3)}{p_{01}p_{10}(b_0+b_1x+b_2x^2)}\cdot \frac{1}{x^{n+1}}, \quad {as}\ n\to \infty, $$

where $1<x<{1}/{p_{11}}$ is the root of

\[V_1\left(t\right)=1-\left(p_{00}+p_{11}\right)t-\left(p_{01}p_{10}-p_{00}p_{11}\right)t^2+p_{01}p_{10}p^{\delta -1}_{00}t^{\delta +1} \]

that is smallest in absolute value, and

\[a_0=-[p_0+\left(p_1p_{10}-p_0p_{11}\right)], \ \ a_1=p_0(p_{00}+p_{11}), \]

\[a_2=p_0\left(p_{01}p_{10}-p_{00}p_{11}\right)+(p_{00}+p_{11})(p_1p_{10}-p_0p_{11}), \]

\[a_3=(p_1p_{10}-p_0p_{11})(p_{01}p_{10}-p_{00}p_{11}),\]

\[b_0=\delta +1, \ \ b_1=-\delta (p_{00}+p_{11}), \ \ b_2=-(\delta -1)(p_{01}p_{10}-p_{00}p_{11}).\]

Proof. Define the function

$$V\left(t\right)=1-p_{11}t-p_{01}p_{10}t^2\sum^{\delta -2}_{i=0}{{(p_{00}t)}^i}.$$

Since $V\left(t\right)$ is a decreasing function in $t\ge 0$ and we have $V\left(0\right)=1$ , ${\mathop{\mathrm{lim}}_{t\to \infty } V\left(t\right)=-\infty}$ , it follows that there exists a unique positive root of $V\left(t\right)$ , say $t=x$ . For all real or complex numbers t with $\left|t\right|<x$ , we have

(22) \begin{equation} \left|p_{11}t+p_{01}p_{10}t^2\sum^{\delta -2}_{i=0}{{(p_{00}t)}^i}\right|<p_{11}x+p_{01}p_{10}x^2\sum^{\delta -2}_{i=0}{{(p_{00}x)}^i}=1-V\left(x\right)=1, \end{equation}

implying that

$$V\left(t\right)\ge 1-\left|p_{11}t+p_{01}p_{10}t^2\sum^{\delta -2}_{i=0}{{(p_{00}t)}^i}\right|>0, \quad \text{for} \ \left|t\right|<x.$$

Therefore, there exist no roots of $V\left(t\right)$ with $\left|t\right|<x$ . Now, if there exists a real or complex number $t_0$ , $\left|t_0\right|=x$ , such that for $t=t_0$ the inequality (22) reduces to an equality, then $t_0=x$ . Hence, x is smaller in absolute value than any other root of $V\left(t\right)$ . Also, we have

\[V\left(1\right)=1-p_{11}-p_{01}p_{10}\sum^{\delta -2}_{i=0}{{p_{00}}^i=p_{10}}p^{\delta -1}_{00}>0,\]

i.e., $V\left(1\right)>V(x)$ , and hence it holds that $x>1$ .

Since

$$V^{\prime}\left(x\right)=-\left[p_{11}+p_{01}p_{10}\sum^{\delta -2}_{i=2} i{p_{00}}^{i-2}x^i\right]\neq 0,$$

it follows that x is a single root of $V\left(t\right)$ . Finally, since

$$V\left({1}/{p_{11}}\right)=-p_{01}p_{10}\sum^{\delta -2}_{i=2}{{p_{00}}^{i-2}p^{-i}_{11}}<0,$$

it holds that $V\left({1}/{p_{11}}\right)<V(x)$ , implying that $({1}/{p_{11})>x}$ . Therefore, x is a single root which is smaller in absolute value than any other root of $V\left(t\right)$ satisfying $1<x<{1}/{p_{11}}$ .

If we consider the function $U\left(t\right)=p_0p^{\delta -1}_{00}t^{\delta }+(p_1p_{10}-p_0p_{11})p^{\delta -1}_{00}t^{\delta +1}$ , then from (16) we have

\[G_{\delta }\left(t\right)=\frac{U(t)}{V(t)}=\frac{U_1(t)}{V_1(t)},\]

where

\[U_1\left(t\right)=\left(1-p_{00}t\right)U(t),\]

\[V_1\left(t\right)=1-\left(p_{00}+p_{11}\right)t-\left(p_{01}p_{10}-p_{00}p_{11}\right)t^2+p_{01}p_{10}p^{\delta -1}_{00}t^{\delta +1}.\]

Therefore, x is also the root of $V_1\left(t\right)$ that is smallest in absolute value, and hence, according to the partial fraction expansion method (see Feller [22, p. 277]), the coefficient of $t^n$ in $G_{\delta }\left(t\right)$ (i.e., the quantity ${f_{\delta }\left(n\right)\mathrm{=Pr} (T_{\delta }=n})$ ) equals (approximately, for large n) ${\rho }_1x^{-(n+1)}$ ; i.e., it holds that

(23) \begin{equation} f_{\delta }\left(n\right)\sim {\rho }_1x^{-(n+1)}, \ \text{as} \ n\to \infty, \end{equation}

where x is a simple root of $V_1\left(t\right)=0$ which is smaller in absolute value than any other root, and the coefficient ${\rho }_1$ is equal to

(24) \begin{equation} {\rho }_1=-U_1(x){\left\{{\left[\frac{dV_1\left(t\right))}{dt}\right]}_{t=x}\right\}}^{-1}. \end{equation}

From $V_1\left(x\right)=0$ , we get $p^{\delta -1}_{00}x^{\delta +1}={[1-\left(p_{00}+p_{11}\right)x-\left(p_{01}p_{10}-p_{00}p_{11}\right)x^2]}/{p_{01}p_{10}}$ , and thus we find

\[\frac{d}{dx}V_1\left(x\right)=-\frac{1}{x}(b_0+b_1x+b_2x^2), U_1\left(x\right)=\left(1-p_{00}x\right)(a_0+a_1x+a_2x^2+a_3x^3). \]

Now the result follows immediately from (23) and (24).

In the sequel, let us examine in more detail the distribution of the lifetime $T_{\delta }$ for the binomial shock process. First, in the following theorem we prove an important property satisfied by $T_{\delta }$ , i.e., that the random variable $T_{\delta }-\delta$ follows a discrete compound geometric distribution. Representation of a distribution as a compound geometric distribution is useful from a probabilistic standpoint, as many properties follow from this, such as infinite divisibility (e.g. Steutel [44]); also, we can easily obtain several other results on the distribution of $T_{\delta }$ , such as recursions for the PMF, the survival function, the moments, bounds, and asymptotics.

Theorem 4.2. For the binomial shock process, the shifted random variable $T_{\delta }-\delta \in \{0$ , 1, 2, $\cdots \}$ follows a discrete compound geometric distribution; that is, $T_{\delta }-\delta \sim CGeo(q^{\delta },\ f_Y)$ , where

(25) \begin{equation} f_Y\left(y\right)=\frac{pq^{y-1}}{1-q^{\delta }}, \qquad y=1, 2, \cdots, \delta, \end{equation}

is the PMF of a truncated Geo(p) distribution.

Proof. Consider the discrete compound geometric sum

\[H=\left\{ \begin{array}{l@{\quad}l} 0& if\ N=0, \\ \\[-8pt] Y_1+Y_2+\cdots Y_N& if\ N\ge 1, \end{array} \right.\]

where the random variable N has the geometric distribution with PMF

\[{\mathrm{Pr} \left(N=n\right)\ }=q^{\delta }{(1-q^{\delta })}^n, \qquad n=0, 1, 2, \cdots, \]

and the random variables $\{Y_i$ , $i\ge 1\}$ are i.i.d. and independent of N with common PMF

\[{\mathrm{Pr} \left(Y=y\right)\ }=\frac{pq^{y-1}}{1-q^{\delta }}, \qquad y=1, 2, \cdots, \delta .\]

If $P_N\left(t\right)=\mathbb{E}[t^N]$ and $P_Y\left(t\right)=\mathbb{E}[t^Y]$ denote the PGFs of N and Y respectively, then

$$P_N\left(t\right)=\frac{q^{\delta }}{1-\left(1-q^{\delta }\right)t} \ \ \text{and} \ \ P_Y\left(t\right)=\frac{pt[1-{\left(qt\right)}^{\delta }]}{(1-q^{\delta })(1-qt)}.$$

Hence, the PGF $P_H\left(t\right)=\mathbb{E}[t^H]$ of the random sum H is

(26) \begin{align} P_H\left(t\right)&=P_N\left[P_Y\left(t\right)\right] \ = \ \frac{q^{\delta }}{1-\left(1-q^{\delta }\right)P_H\left(t\right)} \nonumber\\[3pt] &=\frac{(1-qt)q^{\delta }}{1-t+pq^{\delta }t^{\delta +1}}. \end{align}

Now, since $\mathbb{E}\left[t^{T_{\delta }-\delta }\right]=t^{-\delta }\mathbb{E}\left[t^{T_{\delta }}\right]$ , from (17) and (26) it follows that $\mathbb{E}\left[t^{T_{\delta }-\delta }\right]=P_H\left(t\right)$ , and thus the random variables $T_{\delta }-\delta$ and H have the same distribution; that is, $T_{\delta }-\delta$ has a discrete compound geometric distribution with values in the set $\{0,1,2,\cdots\}$ .

An important immediate consequence of Theorem 4.2 is given in the following corollary, where it is shown that $T_{\delta }-\delta$ belongs to certain discrete reliability classes of distributions. Let N be a nonnegative discrete random variable with $p_n=\mathrm{Pr}\mathrm{}(N=n)$ , $a_n=\mathrm{Pr}\mathrm{}(N>n)$ . The distribution of N is said to be discrete decreasing failure rate (D-DFR) if ${a_{n+1}}/{a_n}$ is nondecreasing in n for all $n\ge 0$ . A discrete failure rate may be defined as

$$h\left(n\right)={\mathrm{Pr} \left(N=n\left|N\ge n\right.\right)\ }=\frac{p_n}{p_n+a_n}, \ \text{for all} \ n\ge 0,$$

and thus ${a_{n+1}}/{a_n}=1-h(n+1)$ , implying that the distribution of N is D-DFR if h(n) is nonincreasing for all $n\ge 1$ . Also, the distribution of N is said to be discrete strongly decreasing failure rate (DS-DFR) if h(n) is nonincreasing for all $n\ge 0$ (see, e.g., Willmot and Cai [48]). It is obvious that the DS-DFR class is a subclass of the D-DFR class. The distribution of N is said to be discrete new worse than used (D-NWU) if $a_{m+n}\ge a_ma_n$ , for $m, n=0$ , 1, 2, $\cdots $ , and is said to be discrete strongly new worse than used (DS-NWU) if $a_{m+n+1}\ge a_ma_n$ , for $m, n=0$ , 1, 2, $\cdots $ (see Cai and Kalashnikov [9]). It is shown in Cai and Kalashnikov [9] that the DS-NWU class is contained in the D-NWU class.

Corollary 4.3. For the binomial shock process, the distribution of the shifted random variable $T_{\delta }-\delta$ is DS-DFR and DS-NWU.

Proof. Since the survival function ${\overline{F}}_Y\left(x\right)\,{=}\,{\mathrm{Pr} \left(Y>x\right)\ }=\sum^{\delta }_{y=x+1}{f_Y(x)}$ , where the PMF of Y is given by (25), is

\[{\overline{F}}_Y\left(x\right)=\frac{q^x-q^{\delta }}{1-q^{\delta }}, \qquad 0\le x\le \delta, \]

it follows that the function

\[h\left(x\right)=\frac{f_Y\left(x\right)}{f_Y\left(x\right)+{\overline{F}}_Y\left(x\right)}=p\frac{q^{x-1}}{q^{x-1}-q^{\delta }}\]

is nonincreasing for all $n\ge 1$ , and hence the distribution of Y is D-DFR. Therefore, from Willmot and Cai [48, Theorem 2.1], it follows that the distribution of $T_{\delta }-\delta$ is DS-DFR. Also, since the random variable $T_{\delta }-\delta$ follows a discrete compound geometric distribution, this implies that $T_{\delta }-\delta$ is NWU (Brown [8]), and hence the result follows from Theorem 2.2 of Willmot and Cai [48].

Using (10), we get a recursion for the PMF of the discrete compound geometric random variable $T_{\delta }-\delta$ which leads to the recursion given by (18) for the PMF $f_{\delta }\left(n\right)=\mathrm{Pr}\mathrm{}(T_{\delta }=n)$ . Also, using (11) (or equivalently, using (18)), we get a recursion for the survival function of $T_{\delta }-\delta$ , from which we obtain that ${\overline{F}}_{\delta }$ $\left(n\right)=\mathrm{Pr}\mathrm{}(T_{\delta }>n)$ satisfies the recursive scheme

\[{\overline{F}}_{\delta }\left(n\right)={\overline{F}}_{\delta }\left(n-1\right)-pq^{\delta }{\overline{F}}_{\delta }\left(n-\delta -1\right), \qquad n\ge 2\delta +1,\]

with initial conditions

\begin{align*}{\overline{F}}_{\delta }\left(n\right)&=1, \qquad 0\le n\le \delta -1 ; \\{\overline{F}}_{\delta }\left(n\right)&=1-[1+\left(n-\delta \right)p]q^{\delta }, \qquad \delta \le n\le 2\delta .\end{align*}

Moreover, using (12) for the random variable $T_{\delta }-\delta$ , we again get the results of (21) as obtained by Bian [6].

In the sequel we shall give an upper bound for the survival function ${\overline{F}}_{\delta }\left(n\right)$ using the fact that $T_{\delta }-\delta$ has a discrete compound geometric distribution.

Corollary 4.4. If $\kappa >1$ satisfies

(27) \begin{equation} 1-\kappa -pq^{\delta }{\kappa }^{\delta +1}=0, \end{equation}

then

\[{\overline{F}}_{\delta }\left(n\right)\le (1-q^{\delta }){\left(\frac{1}{\kappa }\right)}^{n-\delta }, \qquad n\ge \delta .\]

Proof. It is easy to see that if $\kappa >1$ satisfies (27), then it holds that $P_Y\left(\kappa \right)={1}/{(1-q^{\delta })}$ . Also, since the distribution of Y is D-DFR (see the proof of Corollary 4.3), it is also D-NWU (Willmot and Cai [48]), and hence from Willmot and Lin [49, Corollary 7.2.5] we get the following upper bound for the survival function ${\overline{F}}_H\left(x\right)=\mathrm{Pr}\mathrm{}(H>x)$ of the discrete compound geometric random variable $H=T_{\delta }-\delta$ :

\[{\overline{F}}_H\left(x\right)\le {\overline{F}}_H\left(0\right){\left(\frac{1}{\kappa }\right)}^x, \qquad x=0, 1, 2, \cdots. \]

Since ${\overline{F}}_H\left(0\right)={\mathrm{Pr} \left(T_{\delta }>\delta \right)\ }=1-f_{\delta }\left(\delta \right)=1-q^{\delta }$ and ${\overline{F}}_H\left(n-\delta \right)={\overline{F}}_{\delta }\left(n\right)$ , the required upper bound follows immediately.

For the binomial shock process, the asymptotic result of Theorem 4.1 takes a simpler form, as illustrated in the following corollary.

Corollary 4.5. For the binomial shock process, the PMF $f_{\delta }\left(n\right)$ of the lifetime $T_{\delta }$ satisfies

$$ f_{\delta }\left(n\right)\sim \frac{\left(x-1\right)(1-qx)}{p(\delta +1-\delta x)}\cdot \frac{1}{x^{n+1}}, \ {as} \ n\to \infty, $$

where $1<x<{1}/{p}$ is the root of $V_1\left(t\right)=1-t+pq^{\delta }t^{\delta +1}$ that is smallest in absolute value.

Note that $\kappa $ of Corollary 4.4 is exactly the root x of Corollary 4.5. The root x can easily be calculated by solving the equation $V_1\left(t\right)=0$ using the package R. Also, the root x can be satisfactorily approximated by

\[x^*=1+pq^{\delta }[1+\left(\delta +1\right)pq^{\delta }] .\]

To see this, let us write first $V\left(x\right)=0$ in the alternative form

\[x=1+pq^{\delta }x^{\delta +1}=h(x),\]

and observe that the dominant root x can be numerically calculated by successive approximations, setting $x_0=1$ and $x_{k+1}=h(x_k)$ (see, e.g., Feller [22]). The first two iterations yield

\[x_1=h\left(x_0\right)=1+pq^{\delta },\]

\[x_2=h\left(x_1\right)=1+pq^{\delta }{(1+pq^{\delta })}^{\delta +1}\cong 1+pq^{\delta }[1+\left(\delta +1\right)pq^{\delta }]=x^*,\]

and since the higher-step approximations become rather cumbersome, one could terminate the process here (at the price of a cruder approximation as compared to subsequent terms of the iteration scheme).

5. The distributions of $ \boldsymbol{M_\delta} $ and $ \boldsymbol{N_\delta} $

Let $f^{\left(1\right)}_{\delta }\left(m\right)=\mathrm{Pr}\mathrm{}(M_{\delta }=m)$ , $m\ge 0$ , be the PMF of the random variable $M_{\delta }$ . In the following corollary it is shown that $M_{\delta }\sim Geo(p_{10}p^{\delta -1}_{00})$ .

Corollary 5.1. For the Markov shock process, the number of shocks $M_{\delta }$ until the failure of the system follows the geometric distribution with PMF

\[f^{\left(1\right)}_{\delta }\left(m\right)=p_{10}p^{\delta -1}_{00}{\left(1-p_{10}p^{\delta -1}_{00}\right)}^m, \qquad m=0, 1, 2, \cdots. \]

Proof. By letting $z=t=1$ in (15), we get that the PGF $G^{\left(1\right)}_{\delta }\left(u\right)=\mathbb{E}\left[u^{M_{\delta }}\right]$ is given by

\begin{align*} G^{\left(1\right)}_{\delta }\left(u\right)&=\frac{[p_0+\left(p_1p_{10}-p_0p_{11}\right)]p^{\delta -1}_{00}}{1-up_{11}-up_{01}p_{10}\sum^{\delta -2}_{i=0}{{(p_{00})}^i}}\\[3pt] &=\frac{p_{10}p^{\delta -1}_{00}}{1-\left(1-p_{10}p^{\delta -1}_{00}\right)u},\end{align*}

and hence the result follows.

Obviously, from Corollary 5.1 we get that $M_{\delta }\sim Geo(q^{\delta })$ for the binomial shock process (Bian et al. [6]).

Next, let us examine the distribution of the random variable $N_{\delta }$ . We recall that $N_{\delta }$ represents the number of periods in which no shocks appear, up to the failure of the system. By letting $u=t=1$ in (15), we immediately obtain the following result.

Corollary 5.2. (i) For the Markov shock process, the PGF $G^{\left(0\right)}_{\delta }\left(z\right)=\mathbb{E}\left[z^{N_{\delta }}\right]$ of the random variable $N_{\delta }$ is given by

(28) \begin{equation} G^{\left(0\right)}_{\delta }\left(z\right)=\frac{[p_0+\left(p_1p_{10}-p_0p_{11}\right)z]p^{\delta -1}_{00}z^{\delta }}{1-p_{11}-zp_{01}p_{10}\sum^{\delta -2}_{i=0}{{(p_{00}z)}^i}} . \end{equation}

(ii) For the binomial shock process, the PGF $G^{\left(0\right)}_{\delta }\left(z\right)=\mathbb{E}\left[z^{N_{\delta }}\right]$ is given by

(29) \begin{equation} G^{\left(0\right)}_{\delta }\left(z\right)=\frac{(1-qz)q^{\delta -1}z^{\delta }}{1-z+pq^{\delta -1}z^{\delta }} . \end{equation}

Also, from (28) we observe that $N_{\delta }$ has a matrix-geometric distribution, and its PMF and survival function can be computed using (19) and (20) with ( $m=\delta +1$ )

\[Q=\left[ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} -(p_{11}+p_{01}p_{10}) & 0 & 0 & \cdots & 0 & 1 \\ \\[-8pt] 0 & 0 & 0 & \cdots & 0 & 0 \\ \\[-8pt] 0 & 1 & 0 & \cdots & 0 & 0 \\ \\[-8pt] -p_{01}p_{10}p^{\delta -2}_{00} & 0 & 1 & \cdots & 0 & 0 \\ \\[-8pt] \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ \\[-8pt] -p_{01}p_{10}p_{00} & 0 & 0 & \cdots & 1 & 0 \end{array}\right], \ \ \ \ {\boldsymbol{{u}}}^{\prime}=\left[ \begin{array}{c} 0 \\ \\[-8pt] (p_1p_{10}-p_0p_{11})p^{\delta -1}_{00} \\ \\[-8pt] p_0p^{\delta -1}_{00} \\ \\[-8pt] 0 \\ \\[-8pt] \vdots \\ \\[-8pt] 0 \end{array}\right].\]

Rewriting (28) as

\[G^{\left(0\right)}_{\delta }\left(z\right)=\frac{\left(1-p_{00}z\right)[p_0+\left(p_1p_{10}-p_0p_{11}\right)z]p^{\delta -1}_{00}z^{\delta }}{p_{10}[1-z+p_{01}p^{\delta -1}_{00}z^{\delta }]},\]

we can easily proceed to the development of a recursive relationship for the PMF $f^{\left(0\right)}_{\delta }(k)=\mathrm{Pr}\mathrm{}(N_{\delta }=k)$ , as given in the next result.

Corollary 5.3. (i) For the Markov shock process, the PMF $f^{\left(0\right)}_{\delta }(k)=\mathrm{Pr}\mathrm{}(N_{\delta }=k)$ satisfies the recursive scheme

\[f^{\left(0\right)}_{\delta }\left(k\right)=f^{\left(0\right)}_{\delta }\left(k-1\right)-p_{01}p^{\delta -1}_{00}f^{\left(0\right)}_{\delta }(k-\delta ), \qquad k\ge \delta +3,\]

with initial conditions

\begin{align*} f^{\left(0\right)}_{\delta }\left(k\right)&=0, \qquad 0\le k\le \delta -1, \\[3pt] f^{\left(0\right)}_{\delta }\left(\delta \right)&=p_0p^{-1}_{10}p^{\delta -1}_{00}, \\[3pt] f^{\left(0\right)}_{\delta }\left(\delta +1\right)&=p_0p^{-1}_{10}p^{\delta -1}_{00}+(p_1p_{10}-p_0p_{11}-p_0p_{00})p^{-1}_{10}p^{\delta -1}_{00},\\[3pt] f^{\left(0\right)}_{\delta }\left(\delta +2\right)&=p_0p^{-1}_{10}p^{\delta -1}_{00}+\left(p_1p_{10}-p_0p_{11}-p_0p_{00}\right)p^{-1}_{10}p^{\delta -1}_{00}-(p_1p_{10}-p_0p_{11})p^{-1}_{10}p^{\delta -1}_{00}.\end{align*}

(ii) For the binomial shock process, the PMF $f^{\left(0\right)}_{\delta }(k)=\mathrm{Pr}\mathrm{}(N_{\delta }=k)$ satisfies the recursive scheme

\[f^{\left(0\right)}_{\delta }\left(k\right)=f^{\left(0\right)}_{\delta }\left(k-1\right)-pq^{\delta -1}f^{\left(0\right)}_{\delta }(k-\delta ), \qquad k\ge 2\delta +1\]

with initial conditions

\begin{align*} f^{\left(0\right)}_{\delta }\left(k\right)&=0, \qquad 0\le k\le \delta -1, \\[3pt] f^{\left(0\right)}_{\delta }\left(\delta \right)&=q^{\delta -1}, \\[3pt] f^{\left(0\right)}_{\delta }\left(k\right)&=pq^{\delta -1}, \qquad \delta +1\le k\le 2\delta . \end{align*}

In the sequel let us consider the binomial shock process. From (29) we obtain that the shifted random variable $N_{\delta }-\delta$ follows a compound geometric distribution as shown in the next theorem.

Theorem 5.1. For the binomial shock process, the random variable $N_{\delta }-\delta \sim CGeo(q^{\delta -1},\ f_U)$ , where

\[f_U(x)={pq^{x-1}}/{(}1-q^{\delta -1}), \qquad x=1, 2, \cdots, \delta -1.\]

Proof. Consider the compound geometric sum

\[L_{\delta }=\left\{ \begin{array}{l@{\quad}l} 0,& Q_{\delta }=0, \\ \\[-8pt] U_1+U_2+\cdots +U_{Q_{\delta }},& Q_{\delta }\ge 1, \end{array} \right.\]

where the random variable $Q_{\delta }\sim Geo(q^{\delta -1})$ and the i.i.d. random variables $U_1$ , $U_2$ , $\cdots $ have common PMF given by

\[{\mathrm{Pr} \left(U_1=i\right)\ }=\frac{pq^{i-1}}{1-q^{\delta -1}}, \qquad i=1, 2, \cdots, \delta -1.\]

Then the PGF of $L_{\delta }$ is

\[\mathbb{E}\left[z^{L_{\delta }}\right]=\frac{q^{\delta -1}}{1-\left(1-q^{\delta -1}\right)\mathbb{E}[z^{U_1}]},\]

and since

\[\mathbb{E}\left[z^{U_1}\right]=\frac{pz[1-{\left(qz\right)}^{\delta -1}]}{(1-q^{\delta -1})(1-qz)},\]

we obtain

\[\mathbb{E}\left[z^{L_{\delta }}\right]=\frac{(1-qz)q^{\delta -1}}{1-z+pq^{\delta -1}z^{\delta }}.\]

Therefore, from (29) we get

$$\mathbb{E}\left[z^{N_{\delta }-\delta }\right]=G^{\left(0\right)}_{\delta }\left(z\right)z^{-\delta }=\mathbb{E}\left[z^{L_{\delta }}\right],$$

and hence $N_{\delta }-\delta \triangleq L_{\delta }$ . This completes the proof.

Using Theorem 5.1 and (10), we get another equivalent (to that given in Corollary 5.3) recursive relationship for $f^{\left(0\right)}_{\delta }\left(k\right)$ as

\[f^{\left(0\right)}_{\delta }\left(k\right)=p\sum^{k-\delta }_{i=1}{q^{i-1}f^{\left(0\right)}_{\delta }\left(k-i\right)}, \qquad k\ge \delta +1,\]

with $f^{\left(0\right)}_{\delta }\left(k\right)=0$ , $0\le k\le \delta -1$ , and $f^{\left(0\right)}_{\delta }\left(\delta \right)=q^{\delta -1}$ . Also, the mean of $N_{\delta }$ is

\begin{align*} \mathbb{E}\left[N_{\delta }\right]&=\mathbb{E}\left[L_{\delta }\right]+\delta \ = \ \mathbb{E}\left[Q_{\delta }\right]\mathbb{E}\left[U\right]+\delta \nonumber \\[3pt] &=\frac{1-q^{\delta }}{pq^{\delta -1}}. \nonumber\end{align*}

Since ${\overline{F}}_U\left(k\right)={\mathrm{Pr} \left(U>k\right)\ }={(1-q^{\delta -k-1})}/{(1-q^{\delta -1})}$ , $0\le k\le \delta -2$ , and ${\overline{F}}_U\left(k\right)=0$ , $k\ge \delta -1$ , the survival function $\mathrm{Pr}\mathrm{}(L_{\delta }>k)$ satisfies the recursion

\[{\mathrm{Pr} \left(L_{\delta }>k\right)\ }=\left(1-q^{\delta -1}\right)\sum^k_{i=1}{f_U\left(i\right){\mathrm{Pr} \left(L_{\delta }>k-i\right)\ }}+(1-q^{\delta -1}){\overline{F}}_U\left(k\right), \qquad k\ge 1\]

or

\[{\mathrm{Pr} \left(L_{\delta }>k\right)\ }=\left\{ \begin{array}{l@{\quad}r} p\sum^k_{i=1}q^{i-1}\mathrm{Pr} \left(L_{\delta }>k-i\right)+1-q^{\delta -k-1},& 1\le k\le \delta -2, \\ \\[-8pt] p\sum^k_{i=1}{q^{i-1}}\mathrm{Pr} \left(L_{\delta }>k-i\right),& k\ge \delta -1, \end{array}\right.\]

and hence the survival function ${\overline{F}}^{\left(0\right)}_{\delta }(k)=\mathrm{Pr}\mathrm{}(N_{\delta }>k)$ , $k\ge 0$ , can be evaluated recursively through the following recursive scheme:

\[{\overline{F}}^{\left(0\right)}_{\delta }\left(k\right)=\left\{ \begin{array}{l@{\quad}r} p\sum^{k-\delta }_{i=1}q^{i-1}{\overline{F}}^{\left(0\right)}_{\delta }\left(k-i\right)+1-q^{2\delta -k-1},& \delta +1\le k\le 2\delta -2, \\ \\[-8pt] p\sum^{k-\delta }_{i=1}{q^{i-1}}{\overline{F}}^{\left(0\right)}_{\delta }\left(k-i\right),& k\ge 2\delta -1. \end{array}\right. \]

As in the previous section, one can obtain an upper bound and asymptotic results for ${\overline{F}}^{\left(0\right)}_{\delta }\left(k\right)$ . Since the proofs are similar, they are omitted.

Finally, since $L_{\delta }$ is a compound geometric sum, it follows that the shifted random variable $N_{\delta }-\delta$ is DS-DFR and DS-NWU (the proof is similar to that of Corollary 4.3).

6. The binomial discrete mixed censored $\boldsymbol{\delta}$ -shock model

In this section we study the discrete mixed censored $\delta$ -shock model. This model is obtained by combining the discrete censored $\delta$ -shock model studied in the previous sections and the extreme shock model.

Let $N_{\delta,\gamma }$ be the number of periods in which no shocks appear, until the failure of the system. Here we study the joint and marginal distributions of the random variables $N_{\delta,\gamma }$ , $M_{\delta,\gamma }$ , and $T_{\delta,\gamma }$ under the binomial shock process, where $T_{\delta,\gamma }$ and $M_{\delta,\gamma }$ are defined by (4) and (5) respectively.

Theorem 6.1. The joint PGF

$$G^{\left(012\right)}_{\delta,\gamma }\left(z,u,t\right)= \mathbb{E}\left[z^{N_{\delta,\gamma }}u^{M_{\delta,\gamma }}t^{T_{\delta },\gamma }\right]$$

of the random vector $(N_{\delta,\gamma }, M_{\delta,\gamma }, T_{\delta,\gamma })$ for the binomial shock process is given by

(30) \begin{equation} G^{\left(012\right)}_{\delta,\gamma }\left(z,u,t\right)=\frac{\left(1-qzt\right){\left(qzt\right)}^{\delta }+p\overline{G} ( \gamma )ut[1-{\left(qzt\right)}^{\delta }]}{1-qzt-pG\left(\gamma \right)ut[1-{\left(qzt\right)}^{\delta }]}. \end{equation}

Proof. Suppose that $W_{\delta }$ is the waiting time until the event ‘no success occurs within a $\delta$ -length time period from the last success in $I_1$ , $I_2$ , $\cdots $ , or a shock with magnitude larger than $\gamma $ occurs in $I_1$ , $I_2$ , $\cdots $ ’. Then it is obvious that $T_{\delta,\gamma }\triangleq W_{\delta }$ for $\delta \ge 1$ . There are two possible forms for a typical sequence of outcomes for observing $W_{\delta }$ , namely (I) and (II):

1. (I)

   $$\underbrace{FF\cdots F}_{x_1\le \delta -1}\underbrace{S}_{Z_1\le \gamma }\underbrace{FF\cdots F}_{x_2\le \delta -1}\underbrace{S}_{Z_2\le \gamma }\underbrace{FF\cdots F}_{x_3\le \delta -1}\underbrace{S}_{Z_3\le \gamma }\cdots \underbrace{FF\cdots F}_{x_{i-1}\le \delta -1}\underbrace{S}_{Z_{i-1}\le \gamma }\underbrace{FF\cdots F}_{x_i=\delta },$$
   where $x_1$ is the number of Fs until the first S is reached; $x_k$ , for $2\le k\le i-1$ , is the number of Fs between the $(k-1)$ th and the kth success; and $Z_k$ is the magnitude of the kth shock;

2. (II)

   $$\underbrace{FF\cdots F}_{x_1\le \delta -1}\underbrace{S}_{Z_1\le \gamma }\underbrace{FF\cdots F}_{x_2\le \delta -1}\underbrace{S}_{Z_2\le \gamma }\underbrace{FF\cdots F}_{x_3\le \delta -1}\underbrace{S}_{Z_3\le \gamma }\cdots \underbrace{FF\cdots F}_{x_{i-1}\le \delta -1}\underbrace{S}_{Z_{i-1}\le \gamma }\underbrace{FF\cdots F}_{x_i\le \delta -1}\underbrace{S}_{Z_i>\gamma }.$$

Then the contribution of each of the first $i-1$ terms $\underbrace{FF\cdots F}_{x_k\le \delta -1}\underbrace{S}_{Z_k\le \gamma }$ , $1\le k\le i-1$ , in the pattern (I) is

\[\sum^{\delta -1}_{x_k=0}{pG\left(\gamma \right)q^{x_k}z^{x_k}ut^{x_k+1}=pG\left(\gamma \right)ut\frac{1-{(qzt)}^{\delta }}{1-qzt}},\]

the last term $\underbrace{FF\cdots F}_{x_i=\delta }$ contributes $q^{\delta }z^{\delta }t^{\delta }$ , and thus the overall contribution of the pattern (I) to the PGF is

(31) \begin{equation} q^{\delta }z^{\delta }t^{\delta }{\left(pG\left(\gamma \right)ut\frac{1-{(qzt)}^{\delta }}{1-qzt}\right)}^{i-1}. \end{equation}

Similarly, the contribution of the first $i-1$ terms $\underbrace{FF\cdots F}_{x_k\le \delta -1} \ \underbrace{S}_{Z_k\le \gamma }$ , $1\le k\le i-1$ , in the pattern (II) is again

\[pG\left(\gamma \right)ut\frac{1-{(qzt)}^{\delta }}{1-qzt},\]

whereas the contribution of the last term $\underbrace{FF\cdots F}_{x_i\le \delta -1} \ \underbrace{S}_{Z_i>\gamma }$ is

\[\sum^{\delta -1}_{x_i=0}{p\overline{G}\left(\gamma \right)q^{x_i}u^{x_i}t^{x_i+1}=p\overline{G}\left(\gamma \right)ut\frac{1-{(qzt)}^{\delta }}{1-qzt}},\]

and so the overall contribution of the pattern (II) to the PGF is

(32) \begin{equation} p\overline{G}\left(\gamma \right)ut\frac{1-{(qzt)}^{\delta }}{1-qzt}{\left(pG\left(\gamma \right)ut\frac{1-{(qzt)}^{\delta }}{1-qzt}\right)}^{i-1}. \end{equation}

Summing the contributions to the PGF of all possible patterns (I) and (II) from (31) and (32), we get that

\[G^{\left(012\right)}_{\delta,\gamma }\left(z,u,t\right)=\left\{{(qzt)}^{\delta }+p\overline{G}\left(\gamma \right)ut\frac{1-{(qzt)}^{\delta }}{1-qzt}\right\}\sum^{\infty }_{\iota =1}{{\left(pG\left(\gamma \right)ut\frac{1-{(qzt)}^{\delta }}{1-qzt}\right)}^{i-1}},\]

from which (30) follows immediately.

As expected, we observe that for $\gamma \to \infty $ , the PGF in (30) is reduced to the PGF given by Corollary 3.1. Using (30), we directly obtain the joint PGFs of the random vectors $(N_{\delta,\gamma }, T_{\delta,\gamma })$ , $(M_{\delta,\gamma }, T_{\delta,\gamma })$ , and $(N_{\delta,\gamma }, M_{\delta,\gamma })$ , which easily lead to the evaluation of recursions for their joint PMFs and their joint moments. The details are omitted. Let us discuss the distribution of the lifetime $T_{\delta,\gamma }$ . By letting $z=u=1$ in (30) we get the following result.

Corollary 6.1. The PGF $G_{\delta,\gamma }(t)=\mathbb{E}[t^{T_{\delta,\gamma }}]$ of the lifetime $T_{\delta,\gamma }$ is given by

\[G_{\delta,\gamma }\left(t\right)=\frac{\left(1-qt\right){\left(qt\right)}^{\delta }+p\overline{G}(\gamma )t[1-{\left(qt\right)}^{\delta }]}{1-\left[q+pG\left(\gamma \right)\right]t+pq^{\delta }G\left(\gamma \right)t^{\delta +1}}.\]

The PGF of $T_{\delta,\gamma }$ can alternatively be obtained directly from (4). Indeed, by the definition of the lifetime random variable, we have

\begin{align} G_{\delta,\gamma }\left(t\right)&=t^{\delta }\sum^{\infty }_{n=0}{{\left[\mathbb{E}\left(t^X\mathrel{\left|\vphantom{t^X X\le \delta }\right.}X\le \delta \right)\right]}^n{[\mathrm{Pr}\left(X\le \delta \right)]}^n}\mathrm{Pr}\left(X>\delta \right){[\mathrm{Pr}\left(Z\le \gamma \right)\!]}^n \nonumber \\[3pt] &\quad +\sum^{\infty }_{n=0}{{\left[\mathbb{E}\left(t^X\mathrel{\left|\vphantom{t^X X\le \delta }\right.}X\le \delta \right)\right]}^{n+1}{[\mathrm{Pr}\left(X\le \delta \right)]}^{n+1}}{[\mathrm{Pr}\left(Z\le \gamma \right)]}^nPr\left(Z>\gamma \right), \nonumber\end{align}

and thus obtain

\[G_{\delta,\gamma }\left(t\right)=\frac{t^{\delta }\mathrm{Pr}\left(X>\delta \right)+\mathbb{E}\left(t^X\mathrel{\left|\vphantom{t^X X\le \delta }\right.}X\le \delta \right)\mathrm{Pr}\left(X\le \delta \right)\mathrm{Pr}\left(Z>\gamma \right)}{1-\mathbb{E}\left(t^X\mathrel{\left|\vphantom{t^X X\le \delta }\right.}X\le \delta \right)\mathrm{Pr}\left(X\le \delta \right)\mathrm{Pr}\left(Z\le \gamma \right)}.\]

Manifestly,

\[\mathbb{E}\left(t^X\mathrel{\left|\vphantom{t^X X\le \delta }\right.}X\le \delta \right)=\frac{pt(1-{(qt)}^{\delta })}{(1-qt)(1-q^{\delta })},\]

and $\mathrm{Pr}\left(X\le \delta \right)=1-q^{\delta }$ . Hence, we get

\[G_{\delta,\gamma }\left(t\right)=\frac{\left(1-qt\right){\left(qt\right)}^{\delta }+p\overline{G}(\gamma )t[1-{\left(qt\right)}^{\delta }]}{1-\left[q+pG\left(\gamma \right)\right]t+pq^{\delta }G\left(\gamma \right)t^{\delta +1}}.\]

Using Corollary 6.1, one can easily obtain a recursive scheme for the evaluation of the PMF $f_{\delta,\gamma }\left(n\right)=\mathrm{Pr}\mathrm{}(T_{\delta,\gamma }=n)$ .

Corollary 6.2. The PMF $f_{\delta,\gamma }\left(n\right)=\mathrm{Pr}(T_{\delta,\gamma }=n)$ can be evaluated through the recursive formula

\[f_{\delta,\gamma }\left(n\right)=\left[q+pG\left(\gamma \right)\right]f_{\delta,\gamma }\left(n-1\right)-pq^{\delta }G(\gamma )f_{\delta,\gamma }\left(n-\delta -1\right), \qquad n\ge \delta +2\]

with initial conditions

\[ f_{\delta,\gamma }\left(0\right)=0 ; \qquad f_{\delta,\gamma }\left(1\right)=p\overline{G}(\gamma ) ; \qquad f_{\delta,\gamma }\left(n\right)={[q+pG\left(\gamma \right)]}^{n-1}p\overline{G}(\gamma ), \quad 2\le n\le \delta -1; \]

\[ f_{\delta,\gamma }\left(\delta \right)=q^{\delta }+{[q+pG\left(\gamma \right)]}^{\delta -1}p\overline{G}(\gamma ) ; \]

\[ f_{\delta,\gamma }\left(\delta +1\right)=pq^{\delta }\left[G\left(\gamma \right)-\overline{G}\left(\gamma \right)\right]+{[q+pG\left(\gamma \right)\!]}^{\delta }p\overline{G}(\gamma ). \]

Also, from Corollary 6.1 it follows that $T_{\delta,\gamma }$ has a matrix-geometric distribution, and hence an exact relationship for $f_{\delta,\gamma }\left(n\right)$ and ${\overline{F}}_{\delta,\gamma }\left(n\right)=\mathrm{Pr}\mathrm{}(T_{\delta,\gamma }>n)$ can be obtained using (19) and (20) respectively, with ( $m=\delta +1$ )

\[Q=\left[ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} q+pG(\gamma ) & 0 & 0 & \cdots & 0 & 1 \\ \\[-8pt] -pq^{\delta }G(\gamma ) & 0 & 0 & \cdots & 0 & 0 \\ \\[-8pt] 0 & 1 & 0 & \cdots & 0 & 0 \\ \\[-8pt] 0 & 0 & 1 & \cdots & 0 & 0 \\ \\[-8pt] \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ \\[-8pt] 0 & 0 & 0 & \cdots & 1 & 0 \end{array}\right], \ \ \ {\boldsymbol{{u}}}^{\prime}=\left[ \begin{array}{c} p\overline{G}(\gamma ) \\ \\[-8pt] -q^{\delta }(q+p\overline{G}\left(\gamma \right)\!] \\ \\[-8pt] q^{\delta } \\ \\[-8pt] 0 \\ \\[-8pt] \vdots \\ \\[-8pt] 0 \end{array}\right] .\]

By letting $u=t=1$ in (30), we get that the PGF $G^{\left(0\right)}_{\delta }\left(z\right)=\mathbb{E}\left[z^{N_{\delta,\gamma }}\right]$ of the random variable $N_{\delta,\gamma }$ is given by

\[G^{\left(0\right)}_{\delta }\left(z\right)=\frac{\left(1-qz\right){\left(qz\right)}^{\delta }+p\overline{G}(\gamma )[1-{\left(qz\right)}^{\delta }]}{1-qz-pG\left(\gamma \right)[1-{\left(qz\right)}^{\delta }]}.\]

Using this, we can easily compute recursively the PMF, the survival function, and the moments of $N_{\delta,\gamma }$ ; also, we can obtain an exact formula for the PMF and the survival function, since $N_{\delta,\gamma }$ also has a matrix-geometric distribution. The results are straightforward and hence the details are omitted.

Finally, in the following corollary we give the distribution of the number of shocks $M_{\delta,\gamma }$ .

Corollary 6.3. The distribution of the random variable $M_{\delta,\gamma }$ of the number of shocks until the failure of the system is the discrete mixture of the degenerate distribution at zero and the $Geo(\theta ;1)$ distribution with weights $q^{\delta }$ and $1-q^{\delta }$ respectively, where $\theta =1-\left(1-q^{\delta }\right)G(\gamma )$ .

Proof. Letting $z=t=1$ , from (30) we get that the PGF $G^{\left(1\right)}_{\delta,\gamma }\left(u\right)=\mathbb{E}\left[u^{M_{\delta,\gamma }}\right]$ of the random variable $M_{\delta,\gamma }$ is

\[G^{\left(1\right)}_{\delta,\gamma }\left(u\right)=\frac{q^{\delta }+(1-q^{\delta })\overline{G}\gamma )u}{1-\left(1-q^{\delta }\right)G\left(\gamma \right)u},\]

and since it can be equivalently rewritten as

\[G^{\left(1\right)}_{\delta,\gamma }\left(u\right)=q^{\delta }+(1-q^{\delta })\frac{\left[1-\left(1-q^{\delta }\right)G\left(\gamma \right)\right]u}{1-\left(1-q^{\delta }\right)G\left(\gamma \right)u},\]

the proof is completed.

Hence, it follows immediately from Corollary 6.3 that the PMF $f^{\left(1\right)}_{\delta,\gamma }\left(m\right)=\mathrm{Pr}\mathrm{}(M_{\delta,\gamma }=m)$ is given by

\[f^{\left(1\right)}_{\delta,\gamma }\left(m\right)=\left\{ \begin{array}{c@{\quad}l} q^{\delta },& m=0, \\ \left(1-q^{\delta }\right)\left[1-\left(1-q^{\delta }\right)G\left(\gamma \right)\right]{\left[\left(1-q^{\delta }\right)G\left(\gamma \right)\right]}^{m-1},& m=1,\ 2,\ \cdots. \ \ \end{array}\right.\]

For an illustration, in Table 1 we compute the PMF and mean of $T_{\delta,\gamma }$ when $\mathrm{Pr}\left\{Z\le x\right\}=1-{(1-\theta )}^x$ for $\theta =0.1$ , $\gamma =15$ , and selected values of $\delta$ and p.

Table 1. The PMF and mean of $T_{\delta,\gamma }$ .