Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T19:32:08.575Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact sampling for some multi-dimensional queueing models with renewal input

Part of: Markov processes Special processes Probabilistic methods, simulation and stochastic differential equations

Published online by Cambridge University Press:  15 November 2019

Jose Blanchet ,
Yanan Pei  and
Karl Sigman
Jose Blanchet*
Affiliation:
Stanford University
Yanan Pei*
Affiliation:
Columbia University
Karl Sigman*
Affiliation:
Columbia University
*
*Postal address: Department of Management Science and Engineering, Stanford University, Stanford, CA 94305, USA.
**Postal address: Department of Industrial Engineering and Operations Research, Columbia University, New York, NY 10027, USA.
**Postal address: Department of Industrial Engineering and Operations Research, Columbia University, New York, NY 10027, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

Using a result of Blanchet and Wallwater (2015) for exactly simulating the maximum of a negative drift random walk queue endowed with independent and identically distributed (i.i.d.) increments, we extend it to a multi-dimensional setting and then we give a new algorithm for simulating exactly the stationary distribution of a first-in–first-out (FIFO) multi-server queue in which the arrival process is a general renewal process and the service times are i.i.d.: the FIFO GI/GI/c queue with 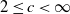$ 2 \leq c \lt \infty$ . Our method utilizes dominated coupling from the past (DCFP) as well as the random assignment (RA) discipline, and complements the earlier work in which Poisson arrivals were assumed, such as the recent work of Connor and Kendall (2015). We also consider the models in continuous time, and show that with mild further assumptions, the exact simulation of those stationary distributions can also be achieved. We also give, using our FIFO algorithm, a new exact simulation algorithm for the stationary distribution of the infinite server case, the GI/GI/ $\infty$ model. Finally, we even show how to handle fork–join queues, in which each arriving customer brings c jobs, one for each server.

Keywords

Exact samplingmulti-server queuerandom walkrandom assignmentdominated coupling from the past

MSC classification

Primary: 65C05: Monte Carlo methods
Secondary: 60K25: Queueing theory 60J05: Discrete-time Markov processes on general state spaces 60K05: Renewal theory 68U20: Simulation
Type
Original Article
Information
Advances in Applied Probability , Volume 51 , Issue 4 , December 2019 , pp. 1179 - 1208
Copyright
© Applied Probability Trust 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asmussen, S. (2008). Applied Probability and Queues (Applications of Mathematics: Stochastic Modelling and Applied Probability 51). Springer.Google Scholar
Asmussen, S., Glynn, P. W. and Thorisson, H. (1992). Stationarity detection in the initial transient problem. ACM Trans. Model. Comput. Simul. 2, 130–157.CrossRefGoogle Scholar
Blanchet, J. and Chen, X. (2015). Steady-state simulation of reflected Brownian motion and related stochastic networks. Ann. Appl. Prob. 25, 3209–3250.CrossRefGoogle Scholar
Blanchet, J. and Dong, J. (2015). Perfect sampling for infinite server and loss systems. Adv. Appl. Prob. 47, 761–786.CrossRefGoogle Scholar
Blanchet, J. H. and Sigman, K. (2011). On exact sampling of stochastic perpetuities. J. Appl. Prob. 48, 165–182.CrossRefGoogle Scholar
Blanchet, J. and Wallwater, A. (2015). Exact sampling of stationary and time-reversed queues. ACM Trans. Model. Comput. Simul. 25, 26.CrossRefGoogle Scholar
Blanchet, J., Dong, J. and Pei, Y. (2018). Perfect sampling of GI/GI/c queues. Queueing Systems 90, 1–33.CrossRefGoogle Scholar
Connor, S. B. and Kendall, W. S. (2015). Perfect simulation of M/G/c queues. Adv. Appl. Prob. 47, 1039–1063.CrossRefGoogle Scholar
Dai, H. (2011). Exact Monte Carlo simulation for fork–join networks. Adv. Appl. Prob. 43, 484–503.CrossRefGoogle Scholar
Flatto, L. and Hahn, S. (1984). Two parallel queues created by arrivals with two demands, I. SIAM J. Appl. Math. 44, 1041–1053.CrossRefGoogle Scholar
Foss, S. (1980). Approximation of multichannel queueing systems. Siberian Math. J. 21, 851–857.CrossRefGoogle Scholar
Foss, S. G. and Chernova, N. I. (2001). On optimality of the FCFS discipline in multiserver queueing systems and networks. Siberian Math. J. 42, 372–385.CrossRefGoogle Scholar
Halfin, S. and Whitt, W. (1981). Heavy-traffic limits for queues with many exponential servers. Operat. Res. 29, 567–588.CrossRefGoogle Scholar
Hillier, F. S. and Lo, F. D. (1972). Tables for multiple-server queueing systems involving Erlang distributions. Technical report, Stanford University, CA.Google Scholar
Kendall, W. S. and Møller, J. (2000). Perfect simulation using dominating processes on ordered spaces, with application to locally stable point processes. Adv. Appl. Prob. 32, 844–865.CrossRefGoogle Scholar
Kiefer, J. and Wolfowitz, J. (1955). On the theory of queues with many servers. Trans. Amer. Math. Soc. 78, 1–18.CrossRefGoogle Scholar
Propp, J. G. and Wilson, D. B. (1996). Exact sampling with coupled Markov chains and applications to statistical mechanics. Random Structures Algorithms 9, 223–252.3.0.CO;2-O>CrossRefGoogle Scholar
Sigman, K. (1988). Regeneration in tandem queues with multiserver stations. J. Appl. Prob. 25, 391–403.CrossRefGoogle Scholar
Sigman, K. (1995). Stationary Marked Point Processes: An Intuitive Approach (Stochastic Modeling Series 2). Taylor & Francis.Google Scholar
Sigman, K. (2011). Exact simulation of the stationary distribution of the FIFO M/G/c queue. J. Appl. Prob. 48, 209–213.CrossRefGoogle Scholar
Sigman, K. (2012). Exact simulation of the stationary distribution of the FIFO M/G/c queue: the general case for. Queueing Systems 70, 37–43.CrossRefGoogle Scholar
Wolff, R. W. (1987). Upper bounds on work in system for multichannel queues. J. Appl. Prob. 24, 547–551.CrossRefGoogle Scholar
Wolff, R. W. (1989). Stochastic Modeling and the Theory of Queues (Prentice Hall International Series in Industrial and Systems Engineering 14). Prentice Hall, Englewood Cliffs, NJ.Google Scholar