Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T07:18:51.218Z Has data issue: false hasContentIssue false
  • English
  • Français

Exponential and gamma form for tail expansions of first-passage distributions in semi-markov processes

Part of: Distribution theory - Probability Special processes

Published online by Cambridge University Press:  14 June 2022

Ronald W. Butler
Ronald W. Butler*
Affiliation:
Southern Methodist University
*
*Postal address: Department of Statistical Science, Southern Methodist University. Email address: rbutler@mail.smu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider residue expansions for survival and density/mass functions of first-passage distributions in finite-state semi-Markov processes (SMPs) in continuous and integer time. Conditions are given which guarantee that the residue expansions for these functions have a dominant exponential/geometric term. The key condition assumes that the relevant states for first passage contain an irreducible class, thus ensuring the same sort of dominant exponential/geometric terms as one gets for phase-type distributions in Markov processes. Essentially, the presence of an irreducible class along with some other conditions ensures that the boundary singularity b for the moment generating function (MGF) of the first-passage-time distribution is a simple pole. In the continuous-time setting we prove that b is a dominant pole, in that the MGF has no other pole on the vertical line 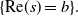$\{\text{Re}(s)=b\}.$ In integer time we prove that b is dominant if all holding-time mass functions for the SMP are aperiodic and non-degenerate. The expansions and pole characterisations address first passage to a single new state or a subset of new states, and first return to the starting state. Numerical examples demonstrate that the residue expansions are considerably more accurate than saddlepoint approximations and can provide a substitute for exact computation above the 75th percentile.

Keywords

Analytic continuationasymptotic hazard ratefirst-passage distributionMarkov processphase-type distrbutionsaddlepoint approximationsemi-Markov processsojourn distribution

MSC classification

Primary: 60K15: Markov renewal processes, semi-Markov processes
Secondary: 60E10: Characteristic functions; other transforms
Type
Original Article
Information
Advances in Applied Probability , Volume 54 , Issue 4 , December 2022 , pp. 1291 - 1319
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Butler, R. W. (2000). Reliabilities for feedback systems and their saddlepoint approximation. Statist. Sci. 15, 279–298.CrossRefGoogle Scholar
Butler, R. W. (2001). First passage distributions in semi-Markov processes and their saddlepoint approximation. In Data Analysis from Statistical Foundations, ed. E. Saleh, Nova Science Publishers, Huntington, NY, pp. 347–368.Google Scholar
Butler, R. W. (2007). Saddlepoint Approximations with Applications. Cambridge University Press.CrossRefGoogle Scholar
Butler, R. W. (2017). Asymptotic expansions and hazard rates for compound and first-passage distributions. Bernoulli 23, 3508–3536.CrossRefGoogle Scholar
Butler, R. W. (2019). Asymptotic expansions and saddlepoint approximations using the analytic continuation of moment generating functions. J. Appl. Prob. 56, 307–338.CrossRefGoogle Scholar
Butler, R. W. (2020). Residue expansions and saddlepoint approximations in stochastic models using the analytic continuation of probability generating functions. Submitted.Google Scholar
Butler, R. W. (2022). Exponential and gamma form for tail expansions of first-passage distributions in semi-Markov processes. Supplementary material. Available at https://doi.org/10.1017/apr.2022.4.CrossRefGoogle Scholar
Butler, R. W. and Wood, A. T. A. (2019). Limiting saddlepoint relative errors in large deviation regions under purely Tauberian conditions. Bernoulli 25, 3379–3399.CrossRefGoogle Scholar
Daniels, H. E. (1954) Saddlepoint approximations in statistics. Ann. Math. Statist. 25, 631–650.CrossRefGoogle Scholar
Daniels, H. (1987). Tail probability approximations. Internat. Statist. Rev. 55, 37–48.CrossRefGoogle Scholar
Doetsch, G. (1974). Introduction to the Theory and Application of the Laplace Transform. Springer, New York.Google Scholar
Feller, W. (1971). An Introduction to Probability Theory and Its Applications, Vol. 2. John Wiley, New York.Google Scholar
Howard, R. A. (1964). System analysis of semi-Markov processes. IEEE Trans. Military Electron. 8, 114–124.CrossRefGoogle Scholar
Howard, R. A. (1971). Dynamic Probabilistic Systems , Vol. II, Semi-Markov and Decision Processes. John Wiley, New York.Google Scholar
Lagakos, S. W., Sommer, C. J., and Zelen, M. (1978). Semi-Markov models for partially censored data. Biometrika 65, 311–317.CrossRefGoogle Scholar
Lugannani, R. and Rice, S. O. (1980). Saddlepoint approximations for the distribution of the sum of independent random variables. Adv. Appl. Prob. 12, 475–490.CrossRefGoogle Scholar
Mason, S. J. (1953). Feedback theory—some properties of signal flow graphs. Proc. Inst. Radio Engineers 41, 1144–1156.CrossRefGoogle Scholar
Mason, S. J. (1956). Feedback theory—further properties of signal flow graphs. Proc. Inst. Radio Engineers 44, 920–926.CrossRefGoogle Scholar
O’Cinneide, C. A. (1990). Characterizations of phase-type distributions. Commun. Statist. Stoch. Models 6, 1–57.CrossRefGoogle Scholar
Phillips, C. L. and Harbor, R. D. (2000). Feedback Control Systems, 4th edn. Prentice Hall, Upper Saddle River, NJ.Google Scholar
Pyke, R. (1961). Markov renewal processes with finitely many states. Ann. Math. Statist. 32, 1243–1259.CrossRefGoogle Scholar
Seneta, E. (2006). Non-negative Matrices and Markov Chains. Springer, New York.Google Scholar
Tijms, H. C. (2003). A First Course in Stochastic Models. John Wiley, New York.CrossRefGoogle Scholar
Supplementary material: PDF

Butler supplementary material

Butler supplementary material

Download Butler supplementary material(PDF)
PDF 390.8 KB