Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Giraitis, L.
and
Surgailis, D.
1991.
Stable Processes and Related Topics.
p.
261.
Giraitis, L.
Molchanov, S. A.
and
Surgailis, D.
1993.
New Directions in Time Series Analysis.
Vol. 46,
Issue. ,
p.
153.
Homble, Patrick
and
McCormick, William P.
1995.
Weak limit results for the extremes of a class of shot noise processes.
Journal of Applied Probability,
Vol. 32,
Issue. 03,
p.
707.
McCormick, William P.
1997.
Extremes for shot noise processes with heavy tailed amplitudes.
Journal of Applied Probability,
Vol. 34,
Issue. 03,
p.
643.
Bakhtin, Yu. Yu.
1998.
The law of the iterated logarithm for the solution of the Burgers equation with random initial data.
Mathematical Notes,
Vol. 64,
Issue. 6,
p.
704.
Бахтин, Юрий Юрьевич
and
Bakhtin, Yuri Yur'evich
1998.
Закон повторного логарифма для решения уравнения Бюргерса со случайными начальными данными.
Математические заметки,
Vol. 64,
Issue. 6,
p.
812.
Ramirez-Perez, Filemon
and
Serfling, Robert
2001.
Shot noise on cluster processes with cluster marks, and studies of long range dependence.
Advances in Applied Probability,
Vol. 33,
Issue. 3,
p.
631.
Iksanov, Aleksander M.
and
Jurek, Zbigniew J.
2003.
Shot Noise Distributions and Selfdecomposability.
Stochastic Analysis and Applications,
Vol. 21,
Issue. 3,
p.
593.
Fasen, Vicky
2005.
Extremes of regularly varying Lévy-driven mixed moving average processes.
Advances in Applied Probability,
Vol. 37,
Issue. 4,
p.
993.
Fasen, Vicky
Klüppelberg, Claudia
and
Lindner, Alexander
2006.
Stochastic Finance.
p.
107.
Fasen, Vicky
2006.
Extremes of subexponential Lévy driven moving average processes.
Stochastic Processes and their Applications,
Vol. 116,
Issue. 7,
p.
1066.
Fasen, Vicky
2009.
Extremes of Lévy driven mixed MA processes with convolution equivalent distributions.
Extremes,
Vol. 12,
Issue. 3,
p.
265.
Fisher, Nicholas I.
2010.
A Conversation with Jef Teugels.
International Statistical Review,
Vol. 78,
Issue. 3,
p.
419.
Matsui, Muneya
and
Mikosch, Thomas
2010.
Prediction in a Poisson cluster model.
Journal of Applied Probability,
Vol. 47,
Issue. 02,
p.
350.
Zhang, Chenhua
and
McCormick, William P.
2012.
Asymptotic properties of the tail distribution and Hill’s estimator for shot noise sequence.
Extremes,
Vol. 15,
Issue. 4,
p.
407.
Matsui, Muneya
2015.
Prediction in a Poisson cluster model with multiple cluster processes.
Scandinavian Actuarial Journal,
Vol. 2015,
Issue. 1,
p.
1.
Baccelli, François
and
Biswas, Anup
2015.
On Scaling Limits of Power Law Shot-Noise Fields.
Stochastic Models,
Vol. 31,
Issue. 2,
p.
187.
Iksanov, Alexander
Marynych, Alexander
and
Meiners, Matthias
2017.
Asymptotics of random processes with immigration I: Scaling limits.
Bernoulli,
Vol. 23,
Issue. 2,
Tillier, C.
2018.
Nonparametric Statistics.
Vol. 250,
Issue. ,
p.
171.
Li, Bo
and
Pang, Guodong
2021.
Shot noise processes with randomly delayed cluster arrivals and dependent noises in the large-intensity regime.
Advances in Applied Probability,
Vol. 53,
Issue. 4,
p.
1190.

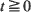 , where
, where 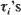 are the points of a renewal process
are the points of a renewal process 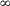 ). In this paper, the extremal properties of {
). In this paper, the extremal properties of {