Hostname: page-component-cb9f654ff-5kfdg Total loading time: 0 Render date: 2025-08-11T20:37:52.726Z Has data issue: false hasContentIssue false
  • English
  • Français

The Λ-Fleming-Viot Process and a Connection with Wright-Fisher Diffusion

Part of: Stochastic processes

Published online by Cambridge University Press:  22 February 2016

Robert C. Griffiths
Robert C. Griffiths*
Affiliation:
Oxford University
*
∗ Postal address: Department of Statistics, University of Oxford, 1 South Parks Road, Oxford OX1 3TG, UK. Email address: griff@stats.ox.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The d-dimensional Λ-Fleming-Viot generator acting on functions g(x ), with x being a vector of d allele frequencies, can be written as a Wright-Fisher generator acting on functions g with a modified random linear argument of x induced by partitioning occurring in the Λ-Fleming-Viot process. The eigenvalues and right polynomial eigenvectors are easy to see from this representation. The two-dimensional process, which has a one-dimensional generator, is considered in detail. A nonlinear equation is found for the Green's function. In a model with genic selection a proof is given that there is a critical selection value such that if the selection coefficient is greater than or equal to the critical value then fixation, when the boundary 1 is hit, has probability 1 beginning from any nonzero frequency. This is an analytic proof different from the proofs of Der, Epstein and Plotkin (2011) and Foucart (2013). An application in the infinitely-many-alleles Λ-Fleming-Viot process is finding an interesting identity for the frequency spectrum of alleles that is based on size biasing. The moment dual process in the Fleming-Viot process is the usual Λ-coalescent tree back in time. The Wright-Fisher representation using a different set of polynomials g n (x) as test functions produces a dual death process which has a similarity to the Kingman coalescent and decreases by units of one. The eigenvalues of the process are analogous to the Jacobi polynomials when expressed in terms of g n (x), playing the role of x n . Under the stationary distribution when there is mutation, 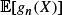is analogous to the nth moment in a beta distribution. There is a d-dimensional version g n (X ), and even an intriguing Ewens' sampling formula analogy when d → ∞.

Keywords

Λ-coalescentFleming-Viot processWright-Fisher diffusion process

MSC classification

Primary: 60G99: None of the above, but in this section
Secondary: 92D15: Problems related to evolution

Information

Type
General Applied Probability
Information
Advances in Applied Probability , Volume 46 , Issue 4 , December 2014 , pp. 1009 - 1035
Copyright
© Applied Probability Trust 

References

Bah, B. and Pardoux, E. (2013). Lambda-lookdown model with selection. Preprint. Available at http://uk.arxiv.org/abs/1303.1953.Google Scholar
Berestycki, N. (2009). Recent Progress in Coalescent Theory (Ensaios Matemáticos 16). Sociedade Brasileira de Matemática, Rio de Janeiro.CrossRefGoogle Scholar
Berestycki, J., Berestycki, N. and Limic, V. (2014a). A small-time coupling between Λ-coalescents and branching processes. Ann. Appl. Prob. 24, 449–475.Google Scholar
Berestycki, J., Berestycki, N. and Limic, V. (2014b). Asymptotic sampling formulae for Λ-coalescents. Ann. Inst. H. Poincaré Prob. Statist. 50, 715–731 Google Scholar
Bertoin, J. and Le Gall, J.-F. (2003). Stochastic flows associated to coalescent processes. Prob. Theory Relat. Fields 126, 261–288.CrossRefGoogle Scholar
Bertoin, J. and Le Gall, J.-F. (2006). Stochastic flows associated to coalescent processes. III. Limit theorems. Illinois J. Math. 50, 147–181.Google Scholar
Birkner, M. and Blath, J. (2009). Measure-valued diffusions, general coalescents and population genetic inference. In Trends in Stochastic Analysis, Cambridge University Press, pp. 329–363.Google Scholar
Birkner, M. et al. (2005). Alpha-stable branching and beta-coalescents. Electron. J. Prob. 10, 303–325.Google Scholar
Cox, D. R. (1970). Renewal Theory. Methuen, London.Google Scholar
Daley, D. J. and Vere-Jones, D. (2003). An Introduction to the Theory of Point Processes, Vol. I, 2nd edn. Springer, New York.Google Scholar
Der, R., Epstein, C. L. and Plotkin, J. B. (2011). Generalized population models and the nature of genetic drift. Theoret. Pop. Biol. 80, 80–99.CrossRefGoogle ScholarPubMed
Der, R., Epstein, C. and Plotkin, J. B. (2012). Dynamics of neutral and selected alleles when the offspring distribution is skewed. Genetics 191, 1331–1344.Google Scholar
Donnelly, P. and Kurtz, T. G. (1996). A countable representation of the Fleming–Viot measure-valued diffusion. Ann. Prob. 24, 698–742.CrossRefGoogle Scholar
Donnelly, P. and Kurtz, T. G. (1999). Particle representations for measure-valued population models. Ann. Prob. 27, 166–205.Google Scholar
Eldon, B. and Wakeley, J. (2006). Coalescent processes when the distribution of offspring number among individuals is highly skewed. Genetics 172, 2621–2633.Google Scholar
Etheridge, A. (2011). Some Mathematical Models from Population Genetics. Springer, Heidelberg.Google Scholar
Etheridge, A. M., Griffiths, R. C. and Taylor, J. E. (2010). A coalescent dual process in a Moran model with genic selection, and the lambda coalescent limit. Theoret. Pop. Biol. 78, 77–92.CrossRefGoogle Scholar
Ewens, W. J. (1972). The sampling theory of selectively neutral alleles. Theoret. Pop. Biol. 3, 87–112.Google Scholar
Ewens, W. J. (2004). Mathematical Population Genetics. I. Theoretical Introduction, 2nd edn. Springer, New York.Google Scholar
Foucart, C. (2013). The impact of selection in the Λ–Wright–Fisher model. Electron. Commun. Prob. 18, no. 72. (Erratum: 19 (2014), no. 15.)CrossRefGoogle Scholar
Griffiths, R. C. (1980). Lines of descent in the diffusion approximation of neutral Wright–Fisher models. Theoret. Pop. Biol. 17, 37–50.Google Scholar
Handa, K. (2014). Stationary distributions for a class of generalized Fleming–Viot processes. Ann. Prob. 42, 1257–1284.Google Scholar
Ismail, M. E. H. (2005). Classical and Quantum Orthogonal Polynomials in One variable (Encyclopedia Math. Appl. 98). Cambridge University Press.Google Scholar
Kimura, M. (1964). Diffusion models in population genetics. J. Appl. Prob. 1, 177–232.Google Scholar
Lessard, S. (2010). Recurrence equations for the probability distribution of sample configurations in exact population genetics models. J. Appl. Prob. 47, 732–751.Google Scholar
Möhle, M. (2006). On sampling distributions for coalescent processes with simultaneous multiple collisions. Bernoulli 12, 35–53.Google Scholar
Möhle, M. and Sagitov, S. (2001). A classification of coalescent processes for haploid exchangeable population models. Ann. Prob. 29, 1547–1562.Google Scholar
Pitman, J. (1999). Coalescents with multiple collisions. Ann. Prob. 27, 1870–1902.Google Scholar
Pitman, J. (2006). Combinatorial Stochastic Processes. Springer, Berlin.Google Scholar
Sagitov, S. (1999). The general coalescent with asynchronous mergers of ancestral lines. J. Appl. Prob. 36, 1116–1125.Google Scholar
Schweinsberg, J. (2000). A necessary and sufficient condition for the Λ-coalescent to come down from infinity. Electron. Commun. Prob. 5, 1–11.Google Scholar
Schweinsberg, J. (2003). Coalescent processes obtained from supercritical Galton–Watson processes. Stoch. Process. Appl. 106, 107–139.CrossRefGoogle Scholar
Tavaré, S. (1984). Line-of-descent and genealogical processes, and their application in population genetics models. Theoret. Pop. Biol. 26, 119–164.Google Scholar