Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Last, G.
and
Schassberger, R.
1998.
On the distribution of the spherical contact vector of stationary germ-grain models.
Advances in Applied Probability,
Vol. 30,
Issue. 01,
p.
36.
Last, G.
and
Schassberger, R.
2000.
On stationary stochastic flows and Palm probabilities of surface processes.
The Annals of Applied Probability,
Vol. 10,
Issue. 2,
Hummel, Hans-Karl
2000.
Homogenization for heat transfer in polycrystals with interfacial resistances.
Applicable Analysis,
Vol. 75,
Issue. 3-4,
p.
403.
2013.
Stochastic Geometry and its Applications.
p.
453.

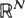 and
and 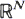 . The pair is jointly stationary, i.e. its distribution is invariant under translations. The vector field
. The pair is jointly stationary, i.e. its distribution is invariant under translations. The vector field 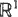 this specializes to a well-known rate conservation law for point processes. As an application, relationships for the linear contact distribution of Φ are derived.
this specializes to a well-known rate conservation law for point processes. As an application, relationships for the linear contact distribution of Φ are derived.