Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T07:07:50.047Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalised birth and death queueing processes: recent results

Published online by Cambridge University Press:  01 July 2016

B. W. Conolly  and
J. Chan
B. W. Conolly
Affiliation:
Chelsea College, University of London
J. Chan
Affiliation:
Chelsea College, University of London
Get access Rights & Permissions [Opens in a new window]

Abstract

The systems considered are single-server, though the theory has wider application to models of adaptive queueing systems. Arrival and service mechanisms are governed by state (n)-dependent mean arrival and service rates λn and µn. It is assumed that the choice of λn and µn leads to a stable regime. Formulae are sought that provide easy means of computing statistics of effectiveness of systems. A measure of traffic intensity is first defined in terms of ‘effective’ service time and inter-arrival intervals. It is shown that the latter have a renewal type connection with appropriately defined mean effective arrival and service rates λ∗ and µ∗ and that in consequence the ratio λ∗/µ∗ is the traffic intensity, equal moreover to 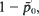where 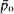is the stable probability of an empty system, consistent with other systems. It is also shown that for first come, first served discipline the equivalent 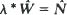of Little's formula holds, where 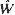and 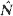are the mean waiting time of an arrival and mean system size at an arbitrary epoch. In addition it appears that stable regime output intervals are statistically identical with effective inter-arrival intervals. Symmetrical moment formulae of arbitrary order are derived algebraically for effective inter-arrival and service intervals, for waiting time, for busy period and for output.

Keywords

ADAPTIVE QUEUEING PROCESSESQUEUEING THEORYGENERALISED BIRTH AND DEATH PROCESSESWAITING TIMEBUSY PERIODOUTPUT–INPUT INTERCHANGE ABILITYLITTLE'S FORMULATRAFFIC INTENSITYEFFECTIVE DISTRIBUTIONS
Type
Research Article
Information
Advances in Applied Probability , Volume 9 , Issue 1 , March 1977 , pp. 125 - 140
Copyright
Copyright © Applied Probability Trust 1977 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Conolly, B. W. (1975) Generalised state dependent Erlangian queues: speculations about calculating measures of effectiveness. J. Appl. Prob. 12, 358–363.Google Scholar
Karlin, S. and McGregor, J. (1957) The classification of birth and death processes. Trans. Amer. Math. Soc. 86, 366–400.Google Scholar
Hadidi, N. and Conolly, B. W. (1969) On the improvement of the operational characteristics of single server queues by use of a queue length dependent mechanism. Appl. Statist. 18, 229–240.CrossRefGoogle Scholar
Conolly, B. W. (1974) The generalised state dependent Erlangian queues. The busy period. J. Appl. Prob. 11, 618–623.Google Scholar
Natvig, B. (1975) On a queueing model where potential customers are discouraged by queue length. Scand. J. Statist. 2, 34–42.Google Scholar
Hadidi, N. (1975) A queueing model with variable arrival rates. Per. Math. Hung. 6, 39–47.Google Scholar
Hadidi, N. (1974) A basically Poisson queue with non-Poisson output. Naval Res. Logist. Quart. 21, 659–662.Google Scholar
Hadidi, N. (1969) On a potentially infinite capacity queueing system. J. Appl. Prob. 6, 594–603.Google Scholar
Natvig, B. (1976) A Contribution to the Theory of Birth-and-Death Queueing Models. , University of Sheffield.Google Scholar