Article contents
Large-time behaviour and the second eigenvalue problem for finite-state mean-field interacting particle systems
Published online by Cambridge University Press: 08 July 2022
Abstract
This article examines large-time behaviour of finite-state mean-field interacting particle systems. Our first main result is a sharp estimate (in the exponential scale) of the time required for convergence of the empirical measure process of the N-particle system to its invariant measure; we show that when time is of the order 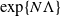 $\exp\{N\Lambda\}$ for a suitable constant
$\exp\{N\Lambda\}$ for a suitable constant 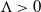 $\Lambda > 0$, the process has mixed well and it is close to its invariant measure. We then obtain large-N asymptotics of the second-largest eigenvalue of the generator associated with the empirical measure process when it is reversible with respect to its invariant measure. We show that its absolute value scales as
$\Lambda > 0$, the process has mixed well and it is close to its invariant measure. We then obtain large-N asymptotics of the second-largest eigenvalue of the generator associated with the empirical measure process when it is reversible with respect to its invariant measure. We show that its absolute value scales as 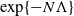 $\exp\{{-}N\Lambda\}$. The main tools used in establishing our results are the large deviation properties of the empirical measure process from its large-N limit. As an application of the study of large-time behaviour, we also show convergence of the empirical measure of the system of particles to a global minimum of a certain ‘entropy’ function when particles are added over time in a controlled fashion. The controlled addition of particles is analogous to the cooling schedule associated with the search for a global minimum of a function using the simulated annealing algorithm.
$\exp\{{-}N\Lambda\}$. The main tools used in establishing our results are the large deviation properties of the empirical measure process from its large-N limit. As an application of the study of large-time behaviour, we also show convergence of the empirical measure of the system of particles to a global minimum of a certain ‘entropy’ function when particles are added over time in a controlled fashion. The controlled addition of particles is analogous to the cooling schedule associated with the search for a global minimum of a function using the simulated annealing algorithm.
Keywords
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust
References
- 1
- Cited by


