Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T14:51:50.853Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit theorems and structural properties of the cat-and-mouse Markov chain and its generalisations

Part of: Limit theorems Markov processes

Published online by Cambridge University Press:  28 February 2022

Sergey Foss ,
Timofei Prasolov  and
Seva Shneer
Sergey Foss*
Affiliation:
Heriot-Watt University and Sobolev Institute of Mathematics
Timofei Prasolov*
Affiliation:
Novosibirsk State University
Seva Shneer*
Affiliation:
Heriot-Watt University and Novosibirsk State University
*
*Postal address: Heriot-Watt University, Edinburgh, EH14 4AS.
**Postal address: Pirogova 1, Novosibirsk State University, Novosibirsk, 630090.
*Postal address: Heriot-Watt University, Edinburgh, EH14 4AS.
Get access Rights & Permissions [Opens in a new window]

Abstract

We revisit the so-called cat-and-mouse Markov chain, studied earlier by Litvak and Robert (2012). This is a two-dimensional Markov chain on the lattice 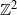$\mathbb{Z}^2$ , where the first component (the cat) is a simple random walk and the second component (the mouse) changes when the components meet. We obtain new results for two generalisations of the model. First, in the two-dimensional case we consider far more general jump distributions for the components and obtain a scaling limit for the second component. When we let the first component be a simple random walk again, we further generalise the jump distribution of the second component. Secondly, we consider chains of three and more dimensions, where we investigate structural properties of the model and find a limiting law for the last component.

Keywords

Cat-and-mouse gamesmultidimensional Markov chaincompound renewal processregular variationweak convergencerandomly stopped sums

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Secondary: 60F05: Central limit and other weak theorems
Type
Original Article
Information
Advances in Applied Probability , Volume 54 , Issue 1 , March 2022 , pp. 141 - 166
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aldous, D. and Fill, J. (2002). Reversible Markov Chains and Random Walks on Graphs. Available at http://www.stat.berkeley.edu/users/aldous/RWG/book.html.Google Scholar
Alsmeyer, G. and Sgibnev, M. (1999). On the tail behaviour of the supremum of a random walk defined on a Markov chain. Yokohama Math. J. 46, 139–159.Google Scholar
Asmussen, S., Henriksen, L. F. and Kloppelberg, C. (1994). Large claims approximations for risk processes in a Markovian environment. Stoch. Process. Appl. 54, 29–43.10.1016/0304-4149(93)00003-XCrossRefGoogle Scholar
Baeza-Yates, R. A., Culberson, J. C. and Rawlins, G. J. E. (1993). Searching in the plane. Inf. Comput. 106, 234–252.10.1006/inco.1993.1054CrossRefGoogle Scholar
Becker-Kern, P., Meerschaert, M. M. and Scheffler, H.-P. (2004). Limit theorems for coupled continuous time random walks. Ann. Prob. 32, 730–756.10.1214/aop/1079021462CrossRefGoogle Scholar
Bingham, N. H., Goldie, C. M. and Teugels, J. L. (1987). Regular Variation (Encyclopaedia Math. Appl. 27). Cambridge University Press.Google Scholar
Borodin, A., Linial, N. and Saks, M. (1992). An optimal online algorithm for metrical task systems. J. Assoc. Comput. Mach. 39, 745–763.10.1145/146585.146588CrossRefGoogle Scholar
Borst, S., Jonckheere, M. and Leskela, L. (2008). Stability of parallel queueing systems with coupled service rates. Discrete Event Dynam. Systems 18, 447–472.10.1007/s10626-007-0021-4CrossRefGoogle Scholar
Coppersmith, D., Doyle, P., Raghavan, P. and Snir, M. (1993). Random walks on weighted graphs and applications to on-line algorithms. J. Assoc. Comput. Mach. 40, 421–453.10.1145/174130.174131CrossRefGoogle Scholar
Denisov, D., Foss, S. and Korshunov, D. (2010). Asymptotics of randomly stopped sums in the presence of heavy tails. Bernoulli 16, 971–994.10.3150/10-BEJ251CrossRefGoogle Scholar
Dobrushin, R. L. (1955). Lemma on the limit of compound random functions. Uspekhi Mat. Nauk 10, 157–159.Google Scholar
Feller, W. (1971a). An Introduction to Probability Theory and Its Applications, Vol. 1. John Wiley, New York.Google Scholar
Feller, W. (1971b). An Introduction to Probability Theory and Its Applications, Vol. 1. John Wiley, New York.Google Scholar
Foss, S., Konstantopoulos, T. and Zachary, S. (2007). Discrete and continuous time modulated random walks with heavy-tailed increments. J. Theoret. Prob. 20, 581–612.10.1007/s10959-007-0081-2CrossRefGoogle Scholar
Foss, S., Shneer, S., Thomas, J. P. and Worrall, T. (2018). Stochastic stability of monotone economies in regenerative environments. J. Econom. Theory 173, 334–360.10.1016/j.jet.2017.11.004CrossRefGoogle Scholar
Foss, S., Shneer, S. and Tyurlikov, A. (2012). Stability of a Markov-modulated Markov chain, with application to a wireless network governed by two protocols. Stoch. Systems 2, 208–231.10.1287/11-SSY030CrossRefGoogle Scholar
Gamarnik, D. (2004). Stochastic bandwidth packing process: stability conditions via Lyapunov function technique. Queueing Systems 48, 339–363.10.1023/B:QUES.0000046581.34849.cfCrossRefGoogle Scholar
Gamarnik, D. and Squillante, M. (2005). Analysis of stochastic online bin packing processes. Stoch. Models 21, 401–425.10.1081/STM-200057127CrossRefGoogle Scholar
Georgiou, N. and Wade, A. R. (2014). Non-homogeneous random walks on a semi-infinite strip. Stoch. Process. Appl. 124, 3179–3205.10.1016/j.spa.2014.05.005CrossRefGoogle Scholar
Hansen, N. R. and Jensen, A. T. (2005). The extremal behaviour over regenerative cycles for Markov additive processes with heavy tails. Stoch. Process. Appl. 115, 579–591.10.1016/j.spa.2004.11.001CrossRefGoogle Scholar
Henry, B. I. and Straka, P. (2011). Lagging and leading coupled continuous time random walks, renewal times and their joint limits. Stoch. Process. Appl. 121, 324–336.Google Scholar
Jelenkovic, P. R. and Lazar, A. A. (1998). Subexponential asymptotics of a Markov-modulated random wwalk with queueing applications. J. Appl. Prob. 35, 325–347.10.1239/jap/1032192851CrossRefGoogle Scholar
Jurlewicz, A., Kern, P., Meerschaert, M. M. and Scheffler, H.-P. (2012). Fractional governing equations for coupled random walks. Comput. Math. Appl. 64, 3021–3036.10.1016/j.camwa.2011.10.010CrossRefGoogle Scholar
Kasahara, Y. (1984). Limit theorems for Lévy processes and Poisson point processes and their applications to Brownian excursions. J. Math. Kyoto Univ. 24, 521–538.Google Scholar
Korshunov, D. (2009). An analog of Wald’s identity for random walks with infinite mean. Siberian Math. J. 50, 663–666.10.1007/s11202-009-0074-8CrossRefGoogle Scholar
Litvak, N. and Robert, P. (2012). A scaling analysis of a cat and mouse Markov chain. Ann. Prob. 22, 792–826.Google Scholar
Lu, Y. and Li, S. (2005). On the probability of ruin in a Markov-modulated risk model. Insurance Math. Econom. 37, 522–532.10.1016/j.insmatheco.2005.05.006CrossRefGoogle Scholar
Manasse, M. S., McGeoch, L. A. and Sleator, D. D. (1990). Competitive algorithms for server problems. J. Algorithms 11, 208–230.10.1016/0196-6774(90)90003-WCrossRefGoogle Scholar
Meerschaert, M. M. and Scheffler, H.-P. (2004). Limit theorems for continuous-time random walks with infinite mean waiting times. J. Appl. Prob. 41, 623–638.10.1239/jap/1091543414CrossRefGoogle Scholar
Shah, D. and Shin, J. (2012). Randomized scheduling algorithm for queueing networks. Ann. Appl. Prob. 22, 128–171.10.1214/11-AAP763CrossRefGoogle Scholar
Skorokhod, A. V. (1956). Limit theorems for stochastic processes. Theory Prob. Appl. 1, 261–290.10.1137/1101022CrossRefGoogle Scholar
Spitzer, F. (1964). Principles of Random Walk. Springer, New York.10.1007/978-1-4757-4229-9CrossRefGoogle Scholar
Uchiyama, K. (2011a). The first hitting time of a single point for random walks. Electron. J. Prob. 16, 1960–2000.10.1214/EJP.v16-931CrossRefGoogle Scholar
Uchiyama, K. (2011b). One dimensional lattice random walks with absorption at a point/on a half line. J. Math. Soc. Japan 63, 675–713.10.2969/jmsj/06320675CrossRefGoogle Scholar
Whitt, W. (2002). Stochastic-Process Limits. Springer, New York.10.1007/b97479CrossRefGoogle Scholar