Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T07:18:33.995Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit theorems for critical branching processes in a finite-state-space Markovian environment

Part of: Limit theorems Markov processes

Published online by Cambridge University Press:  01 March 2022

Ion Grama ,
Ronan Lauvergnat  and
Émile Le Page
Ion Grama*
Affiliation:
Université de Bretagne-Sud, CNRS UMR 6205, LMBA
Ronan Lauvergnat*
Affiliation:
Université de Bretagne-Sud, CNRS UMR 6205, LMBA
Émile Le Page*
Affiliation:
Université de Bretagne-Sud, CNRS UMR 6205, LMBA
*
*Postal address: Université de Bretagne-Sud, CNRS UMR 6205, Laboratoire de Mathématique de Bretagne Atlantique, Campus de Tohannic, BP573, 56017 Vannes, France.
*Postal address: Université de Bretagne-Sud, CNRS UMR 6205, Laboratoire de Mathématique de Bretagne Atlantique, Campus de Tohannic, BP573, 56017 Vannes, France.
*Postal address: Université de Bretagne-Sud, CNRS UMR 6205, Laboratoire de Mathématique de Bretagne Atlantique, Campus de Tohannic, BP573, 56017 Vannes, France.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 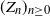$(Z_n)_{n\geq 0}$ be a critical branching process in a random environment defined by a Markov chain 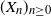$(X_n)_{n\geq 0}$ with values in a finite state space 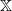$\mathbb{X}$ . Let 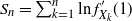$ S_n = \sum_{k=1}^n \ln f_{X_k}^{\prime}(1)$ be the Markov walk associated to 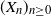$(X_n)_{n\geq 0}$ , where 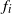$f_i$ is the offspring generating function when the environment is 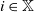$i \in \mathbb{X}$ . Conditioned on the event 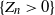$\{ Z_n>0\}$ , we show the nondegeneracy of the limit law of the normalized number of particles 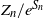${Z_n}/{e^{S_n}}$ and determine the limit of the law of 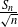$\frac{S_n}{\sqrt{n}} $ jointly with 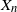$X_n$ . Based on these results we establish a Yaglom-type theorem which specifies the limit of the joint law of 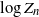$ \log Z_n$ and 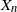$X_n$ given 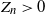$Z_n>0$ .

Keywords

Critical branching processMarkovian environmentconditioned limit theoremsYaglom-type theorem

MSC classification

Primary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.) 60F05: Central limit and other weak theorems
Secondary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Type
Original Article
Information
Advances in Applied Probability , Volume 54 , Issue 1 , March 2022 , pp. 111 - 140
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afanasyev, V. I. (2009). Limit theorems for a moderately subcritical branching process in a random environment. Discrete Math. Appl. 8, 35–52.Google Scholar
Agresti, A. (1974). Bounds on the extinction time distribution of a branching process. Adv. Appl. Prob. 6, 322–335.10.2307/1426296CrossRefGoogle Scholar
Alsmeyer, G. (1994). On the Markov renewal theorem. Stoch. Process. Appl. 50, 37–56.10.1016/0304-4149(94)90146-5CrossRefGoogle Scholar
Athreya, K. B. and Karlin, S. (1971). On branching processes with random environments I: extinction probabilities. Ann. Math. Statist. 42, 1499–1520.10.1214/aoms/1177693150CrossRefGoogle Scholar
Athreya, K. B. and Karlin, S. (1971). Branching processes with random environments II: limit theorems. Ann. Math. Statist. 42, 1843–1858.10.1214/aoms/1177693051CrossRefGoogle Scholar
Athreya, K. B. and Ney, P. E. (1972). Branching Processes. Springer, Berlin, Heidelberg.10.1007/978-3-642-65371-1CrossRefGoogle Scholar
Dekking, F. M. (1987) On the survival probability of a branching process in a finite state i.i.d. environment. Stoch. Process. Appl. 27, 151–157.Google Scholar
D’Souza, J. C. and Hambly, B. M. (1997). On the survival probability of a branching process in a random environment. Adv. Appl. Prob. 29, 38–55.10.2307/1427860CrossRefGoogle Scholar
Geiger, J. and Kersting, G. (2001). The survival probability of a critical branching process in a random environment. Theory Prob. Appl. 45, 517–525.10.1137/S0040585X97978440CrossRefGoogle Scholar
Geiger, J., Kersting, G. and Vatutin, V. A. (2003). Limit theorems for subcritical branching processes in random environment. Ann. Inst. H. Poincaré Prob. Statist. 39, 593–620.10.1016/S0246-0203(02)00020-1CrossRefGoogle Scholar
Grama, I., Lauvergnat, R. and Le Page, é. (2016). Limit theorems for affine Markov walks conditioned to stay positive. Ann. Inst. H. Poincaré Prob. Statist. 54, 529–568.Google Scholar
Grama, I., Lauvergnat, R. and Le Page, É. (2018). Limit theorems for Markov walks conditioned to stay positive under a spectral gap assumption. Ann. Prob. 46, 1807–1877.10.1214/17-AOP1197CrossRefGoogle Scholar
Grama, I., Lauvergnat, R. and Le Page, É. (2019). The survival probability of critical and subcritical branching processes in finite state Markovian environment. Stoch. Process. Appl. 129, 2485–2527.10.1016/j.spa.2018.07.016CrossRefGoogle Scholar
Grama, I., Lauvergnat, R. and Le Page, É. (2020). Conditioned local limit theorems for random walks defined on finite Markov chains. Prob. Theory Relat. Fields 176, 669–735.10.1007/s00440-019-00948-8CrossRefGoogle Scholar
Grama, I., Le Page, É. and Peigné, M. (2017). Conditioned limit theorems for products of random matrices. Prob. Theory Relat. Fields 168, 601–639.10.1007/s00440-016-0719-zCrossRefGoogle Scholar
Guivarc’h, Y. and Liu, Q. (2001). Propriétés asymptotiques des processus de branchement en environnement aléatoire. C. R. Acad. Sci. Paris 332, 339–344.10.1016/S0764-4442(00)01783-3CrossRefGoogle Scholar
Harris, T. E. (1963). The Theory of Branching Processes. Springer, Berlin, Heidelberg.10.1007/978-3-642-51866-9CrossRefGoogle Scholar
Kersting, G. (2020). A unifying approach to branching processes in varying environment. J. Appl. Prob. 57, 196–220.10.1017/jpr.2019.84CrossRefGoogle Scholar
Kersting, G. and Vatutin, V. (2017). Discrete Time Branching Processes in Random Environment. Wiley, London.10.1002/9781119452898CrossRefGoogle Scholar
Kozlov, M. V. (1977). On the asymptotic behavior of the probability of non-extinction for critical branching processes in a random environment. Theory Prob. Appl. 21, 791–804.10.1137/1121091CrossRefGoogle Scholar
Kozlov, M. V. (1995). A conditional function limit theorem for critical branching processes in a random medium. Dokl. Akad. Nauk 344, 12–15.Google Scholar
Liu, Q. (1996). On the survival probability of a branching process in a random environment. Ann. Inst. H. Poincaré Prob. Statist. 32, 1–10.Google Scholar
Shurenkov, V. M. (1984). On the theory of Markov renewal. Theory Prob. Appl. 29, 247–265.10.1137/1129036CrossRefGoogle Scholar
Smith, W. L. and Wilkinson, W. E. (1969). On branching processes in random environments. Ann. Math. Statist. 40, 814–827.10.1214/aoms/1177697589CrossRefGoogle Scholar