Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sawyer, Stanley
1977.
On the past history of an allele now known to have frequency p.
Journal of Applied Probability,
Vol. 14,
Issue. 03,
p.
439.
1986.
Markov Processes.
p.
508.
Nagylaki, Thomas
1986.
Evolutionary Processes and Theory.
p.
629.
Darden, T.
Kaplan, N. L.
and
Hudson, R. R.
1989.
A numerical method for calculating moments of coalescent times in finite populations with selection.
Journal of Mathematical Biology,
Vol. 27,
Issue. 3,
p.
355.
Nagylaki, Thomas
1990.
Models and approximations for random genetic drift.
Theoretical Population Biology,
Vol. 37,
Issue. 1,
p.
192.
Fort, Jean-Claude
and
Pagès, Gilles
1999.
Asymptotic Behavior of a Markovian Stochastic Algorithm with Constant Step.
SIAM Journal on Control and Optimization,
Vol. 37,
Issue. 5,
p.
1456.
Forien, Raphaël
and
Penington, Sarah
2017.
A central limit theorem for the spatial $\Lambda $-Fleming-Viot process with selection.
Electronic Journal of Probability,
Vol. 22,
Issue. none,
Ying, Lei
2018.
On the Approximation Error of Mean-Field Models.
Stochastic Systems,
Vol. 8,
Issue. 2,
p.
126.
Bräutigam, Camila
and
Smerlak, Matteo
2022.
Diffusion approximations in population genetics and the rate of Muller’s ratchet.
Journal of Theoretical Biology,
Vol. 550,
Issue. ,
p.
111236.
Favero, Martina
and
Jenkins, Paul A.
2025.
Sampling probabilities, diffusions, ancestral graphs, and duality under strong selection.
Electronic Journal of Probability,
Vol. 30,
Issue. none,

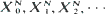 be a real-valued stationary process, and let
be a real-valued stationary process, and let 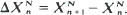 . Suppose that
. Suppose that 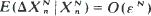 and var, where
and var, where 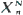 as
as 