Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T07:46:26.040Z Has data issue: false hasContentIssue false
  • English
  • Français

Local properties of random mappings with exchangeable in-degrees

Part of: Combinatorial probability Graph theory Limit theorems

Published online by Cambridge University Press:  01 July 2016

Jennie C. Hansen  and
Jerzy Jaworski
Jennie C. Hansen*
Affiliation:
Heriot-Watt University
Jerzy Jaworski*
Affiliation:
Adam Mickiewicz University
*
∗ Postal address: Department of Actuarial Mathematics and Statistics and the Maxwell Institute for Mathematical Sciences, Heriot-Watt University, Edinburgh EH14 4AS, UK. Email address: j.hansen@ma.hw.ac.uk
∗∗ Postal address: Faculty of Mathematics and Computer Science, Adam Mickiewicz University, Umultowska 87, 61-614 Poznań, Poland. Email address: jaworski@amu.edu.pl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we investigate the ‘local’ properties of a random mapping model, TnD̂, which maps the set {1, 2, …, n} into itself. The random mapping TnD̂, which was introduced in a companion paper (Hansen and Jaworski (2008)), is constructed using a collection of exchangeable random variables D̂1, …, D̂n which satisfy 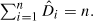In the random digraph, GnD̂, which represents the mapping TnD̂, the in-degree sequence for the vertices is given by the variables D̂1, D̂2, …, D̂n, and, in some sense, GnD̂ can be viewed as an analogue of the general independent degree models from random graph theory. By local properties we mean the distributions of random mapping characteristics related to a given vertex v of GnD̂ - for example, the numbers of predecessors and successors of v in GnD̂. We show that the distribution of several variables associated with the local structure of GnD̂ can be expressed in terms of expectations of simple functions of D̂1, D̂2, …, D̂n. We also consider two special examples of TnD̂ which correspond to random mappings with preferential and anti-preferential attachment, and determine, for these examples, exact and asymptotic distributions for the local structure variables considered in this paper. These distributions are also of independent interest.

Keywords

Random mappinglocal structureexchangeable in-degrees

MSC classification

Primary: 60C05: Combinatorial probability
Secondary: 60F05: Central limit and other weak theorems 05C80: Random graphs
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 40 , Issue 1 , March 2008 , pp. 183 - 205
Copyright
Copyright © Applied Probability Trust 2008 

References

Arney, J. and Bender, E. A. (1982). Random mappings with constraints on coalescence and number of origins. Pacific J. Math. 103, 269–294.Google Scholar
Arratia, R., Stark, D. and Tavaré, S. (1995). Total variation asymptotics for Poisson process approximations of logarithmic combinatorial assemblies. Ann. Prob. 23, 1347–1388.Google Scholar
Berg, S. (1981). On snowball sampling, random mappings and related problems. J. Appl. Prob. 18, 283–290.Google Scholar
Berg, S. (1983). Random contact processes, snowball sampling and factorial series distributions. J. Appl. Prob. 20, 31–46.Google Scholar
Berg, S. and Jaworski, J. (1992). Probability distributions related to the local structure of a random mapping. In Random Graphs, eds Frieze, A. and Łuczak, T., John Wiley, New York, pp. 1–21.Google Scholar
Berg, S. and Mutafchiev, L. (1990). Random mappings with an attracting center: Lagrangian distributions and a regression function. J. Appl. Prob. 27, 622–636.Google Scholar
Burtin, Y. D. (1980). On a simple formula for random mappings and its applications. J. Appl. Prob. 17, 403–414.Google Scholar
Flajolet, P. and Odlyzko, A. M. (1990). Random mapping statistics. In Advances in Cryptology—EUROCRYPT'89 (Lecture Notes Comput. Sci. 434), Springer, Berlin, pp. 329–354.Google Scholar
Hansen, J. C. and Jaworski, J. (2008). Random mappings with exchangeable in-degrees. To appear in Random Structures Algorithms.Google Scholar
Hansen, J. C. and Jaworski, J. (2008). A random mapping with preferential attachment. Submitted.Google Scholar
Jaworski, J. (1990). Random mappings with independent choices of the images. In Random Graphs, Vol. 1, John Wiley, New York, pp. 89–101.Google Scholar
Jaworski, J. (1998). Predecessors in a random mapping. Random Structures Algorithms 13, 501–519.Google Scholar
Jaworski, J. (1999). Epidemic processes on digraphs of random mappings. J. Appl. Prob. 36, 780–798.Google Scholar
Johnson, N. L., Kotz, S. and Kemp, A. W. (1992). Univariate Discrete Distributions, 2nd edn. John Wiley, New York.Google Scholar
Kolchin, V. F. (1986). Random Mappings. Optimization Software, New York.Google Scholar
Mutafčiev, L. (1982). A limit distribution related to random mappings and its application to an epidemic process. Serdica 8, 197–203.Google Scholar
Mutafčiev, L. (1984). On some stochastic problems of discrete mathematics. In Proc. Math. Math. Education (Sunny Beach, 1984), Akad. Nauk, Sofia, pp. 57–80.Google Scholar
Pittel, B. (1983). On distributions related to transitive closures of random finite mappings. Ann. Prob. 11, 428–441.Google Scholar
Prüfer, H. (1918). Neuer Beweis eines Satzes uber Permutationen. Archiv Math. Phys. 27, 142–144.Google Scholar
Quisquater, J.-J. and Delescaille, J.-P. (1990). How easy is collision search? Application to DES. In Advances in Cryptology—Eurocrypt'89 (Lecture Notes Comput. Sci. 434), Springer, Berlin, pp. 429–434.Google Scholar
Van Oorschot, P. C. and Wiener, M. J. (1994). Parallel collision search with applications to hash functions and discrete logarithms. In Proc. 2nd ACM Conf. Comput. Commun. Security, ACM, New York, pp. 210–218.Google Scholar