Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Heinrich, Lothar
2015.
Gaussian limits of empirical multiparameter K-functions of homogeneous Poisson processes and tests for complete spatial randomness.
Lithuanian Mathematical Journal,
Vol. 55,
Issue. 1,
p.
72.
Hug, Daniel
Thäle, Christoph
and
Weil, Wolfgang
2015.
Intersection and proximity of processes of flats.
Journal of Mathematical Analysis and Applications,
Vol. 426,
Issue. 1,
p.
1.
Bourguin, Solesne
Durastanti, Claudio
Marinucci, Domenico
and
Peccati, Giovanni
2016.
Gaussian approximation of nonlinear statistics on the sphere.
Journal of Mathematical Analysis and Applications,
Vol. 436,
Issue. 2,
p.
1121.
Hug, Daniel
Last, Günter
and
Schulte, Matthias
2016.
Second-order properties and central limit theorems for geometric functionals of Boolean models.
The Annals of Applied Probability,
Vol. 26,
Issue. 1,
Schulte, Matthias
2016.
Normal Approximation of Poisson Functionals in Kolmogorov Distance.
Journal of Theoretical Probability,
Vol. 29,
Issue. 1,
p.
96.
Geiss, Christel
and
Labart, Céline
2016.
Simulation of BSDEs with jumps by Wiener Chaos expansion.
Stochastic Processes and their Applications,
Vol. 126,
Issue. 7,
p.
2123.
Geiss, Christel
and
Labart, Céline
2017.
Erratum to “Simulation of BSDEs with jumps by Wiener Chaos expansion” [Stochastic Process. Appl. 126 (2016) 2123–2162].
Stochastic Processes and their Applications,
Vol. 127,
Issue. 3,
p.
1042.
Večeřa, Jakub
and
Beneš, Viktor
2017.
Approaches to asymptotics for U-statistics of Gibbs facet processes.
Statistics & Probability Letters,
Vol. 122,
Issue. ,
p.
51.
Jansen, S.
2019.
Cluster Expansions for GIBBS Point Processes.
Advances in Applied Probability,
Vol. 51,
Issue. 4,
p.
1129.
Schulte, Matthias
and
Yukich, J.E.
2019.
Multivariate second order Poincaré inequalities for Poisson functionals.
Electronic Journal of Probability,
Vol. 24,
Issue. none,
Di Tella, P.
and
Geiss, C.
2020.
Product and moment formulas for iterated stochastic integrals (associated with Lévy processes).
Stochastics,
Vol. 92,
Issue. 6,
p.
969.
Basse-O’Connor, Andreas
Podolskij, Mark
and
Thäle, Christoph
2020.
A Berry–Esseén theorem for partial sums of functionals of heavy-tailed moving averages.
Electronic Journal of Probability,
Vol. 25,
Issue. none,
Herold, Felix
Hug, Daniel
and
Thäle, Christoph
2021.
Does a central limit theorem hold for the k-skeleton of Poisson hyperplanes in hyperbolic space?.
Probability Theory and Related Fields,
Vol. 179,
Issue. 3-4,
p.
889.
Azmoodeh, Ehsan
Ljungdahl, Mathias Mørck
and
Thäle, Christoph
2022.
Multi-dimensional normal approximation of heavy-tailed moving averages.
Stochastic Processes and their Applications,
Vol. 145,
Issue. ,
p.
308.
Klatt, Michael Andreas
and
Last, Günter
2022.
On strongly rigid hyperfluctuating random measures.
Journal of Applied Probability,
Vol. 59,
Issue. 4,
p.
948.
Baci, Anastas
Bonnet, Gilles
and
Thäle, Christoph
2022.
Weak convergence of the intersection point process of Poisson hyperplanes.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 58,
Issue. 2,
Betken, Carina
Hug, Daniel
and
Thäle, Christoph
2023.
Intersections of Poisson k-flats in constant curvature spaces.
Stochastic Processes and their Applications,
Vol. 165,
Issue. ,
p.
96.
Hug, Daniel
and
Schneider, Rolf
2024.
Poisson Hyperplane Tessellations.
p.
449.
Di Tella, Paolo
Geiss, Christel
and
Steinicke, Alexander
2024.
Product formulas for multiple stochastic integrals associated with Lévy processes.
Collectanea Mathematica,
Adamczak, Radosław
Pivovarov, Peter
and
Simanjuntak, Paul
2024.
Limit theorems for the volumes of small codimensional random sections of ℓpn-balls.
The Annals of Probability,
Vol. 52,
Issue. 1,
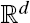 .
.
