Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T11:17:09.865Z Has data issue: false hasContentIssue false
  • English
  • Français

Monotonicity results for queues with doubly stochastic Poisson arrivals: Ross's conjecture

Published online by Cambridge University Press:  01 July 2016

Cheng-Shang Chang ,
Xiu Li Chao  and
Michael Pinedo
Cheng-Shang Chang*
Affiliation:
IBM Thomas J. Watson Research Center
Xiu Li Chao*
Affiliation:
New Jersey Institute of Technology
Michael Pinedo*
Affiliation:
Columbia University
*
∗Postal address: IBM Research Division, T. J. Watson Research Center, H2-K06, P.O. Box 704, Yorktown Heights, NY 10598, USA.
∗∗Postal address: Dept. of Industrial and Management Engineering, New Jersey Institute of Technology, Newark, NJ 07102, USA.
∗∗∗Dept. of Industrial Engineering and Operations Research, Columbia University, New York, NY 10027, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we compare queueing systems that differ only in their arrival processes, which are special forms of doubly stochastic Poisson (DSP) processes. We define a special form of stochastic dominance for DSP processes which is based on the well-known variability or convex ordering for random variables. 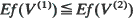For two DSP processes that satisfy our comparability condition in such a way that the first process is more ‘regular' than the second process, we show the following three results: (i) If the two systems are DSP/GI/1 queues, then for all f increasing convex, with V(i), i = 1 and 2, representing the workload (virtual waiting time) in system. (ii) If the two systems are DSP/M(k)/1→ /M(k)/l ∞ ·· ·∞ /M(k)/1 tandem systems, with M(k) representing an exponential service time distribution with a rate that is increasing concave in the number of customers, k, present at the station, then 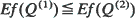for all f increasing convex, with Q(i), i = 1 and 2, being the total number of customers in the two systems. (iii) If the two systems are DSP/M(k)/1/N systems, with N being the size of the buffer, then 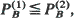where 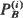denotes the blocking (loss) probability of the two systems. A model considered before by Ross (1978) satisfies our comparability condition; a conjecture stated by him is shown to be true.

Keywords

STOCHASTIC CONVEXITYDOUBLY STOCHASTIC POISSON PROCESSVARIABILITY ORDERING
Type
Research Article
Information
Advances in Applied Probability , Volume 23 , Issue 1 , March 1991 , pp. 210 - 228
Copyright
Copyright © Applied Probability Trust 1991 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chang, C. S. (1989) Comparison theorems for queueing systems and their applications to ISDN. Ph.D. dissertation, Dept. of Electrical Engineering, Columbia University, New York.Google Scholar
Chang, C. S. and Pinedo, M. (1990) Bounds and inequalities for single server loss systems. Queueing Systems 6, 425–436.Google Scholar
Chang, C. S., Chao, X. L. and Pinedo, M. (1990) Integration of discrete-time correlated Markov processes in a TDM system: structural results. Prob. Eng. Inf. Sci. 4, 29–56.CrossRefGoogle Scholar
Fond, S. and Ross, S. M. (1978) A heterogeneous arrival and service queueing loss model. Naval Res. Logist. Quart. 25, 483–488.CrossRefGoogle Scholar
Karatzas, I. and Shreve, S. E. (1988) Brownian Motion and Stochastic Calculus. Springer-Verlag, New York.Google Scholar
Keilson, T. (1979) Markov Chain Models–Rarity and Exponentiality. Springer-Verlag, New York.CrossRefGoogle Scholar
Marshall, A. W. and Olkin, I. (1979) Inequalities—Theory of Majorization and its Applications . Academic Press, New York.Google Scholar
Niu, S.-C. (1980) A single server queueing loss model with heterogeneous arrival and service. Operat. Res. 28, 584–593.Google Scholar
Rolski, T. (1981) Queues with non-stationary input stream: Ross's conjecture. Adv. Appl. Prob. 13, 603–618.Google Scholar
Rolski, T. (1983) Comparison theorems for queues with dependent inter-arrival times. Modelling and Performance Evaluation, Proceeding of the International Seminar, Paris , 42–67.Google Scholar
Rolski, T. (1986) Upper bounds for single server queues with doubly stochastic Poisson arrivals. Math. Operat. Res. 11, 442–450.CrossRefGoogle Scholar
Rolski, T. (1989) Queues with nonstationary arrivals. Queueing Systems 5, 113–130.CrossRefGoogle Scholar
Ross, S. M. (1978) Average delay in queues with non-stationary Poisson arrivals. J. Appl. Prob. 15, 602–609.Google Scholar
Ross, S. M. (1983) Stochastic Processes. Wiley, New York.Google Scholar
Shakred, M. and Shanthikumar, J. G. (1988a) Temporal stochastic convexity and concavity. Stoch. Proc. Appl. 27, 1–20.CrossRefGoogle Scholar
Shaked, M. and Shanthikumar, J. G. (1988b) Stochastic convexity and its applications. Adv. Appl. Prob. 20, 427–446.Google Scholar
Shaked, M. and Shanthikumar, J. G. (1988c) Parametric stochastic convexity and concavity of stochastic processes. Technical Report, Univ. of California, Berkeley.Google Scholar
Shanthikumar, J. G. (1988) Regularity of stochastic processes: A theory based on directional convexity. Technical Report, Univ. of California, Berkeley.Google Scholar
Stoyan, D. (1983). Comparison Methods for Queues and Other Stochastic Models. Wiley, New York.Google Scholar
Svoronos, A. and Green, L. (1987) The N-seasons S-servers loss system. Naval Res. Logist. Quart. 34, 579–591.3.0.CO;2-K>CrossRefGoogle Scholar
Svoronos, A. and Green, L. (1988) A convexity result for single serve exponential loss systems with nonstationary arrivals. J. Appl. Prob. 25, 224–227.Google Scholar