Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T17:14:32.474Z Has data issue: false hasContentIssue false
  • English
  • Français

Nearest-neighbor graphs on the cantor set

Part of: Limit theorems Geometric probability and stochastic geometry

Published online by Cambridge University Press:  01 July 2016

Nathan Shank
Nathan Shank*
Affiliation:
Moravian College
*
∗ Postal address: Mathematics and Computer Science Department, 1200 Main Street, Bethlehem, PA 18018, USA. Email address: shank@math.moravian.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

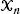Let be a collection of 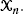n uniform, independent, and identically distributed points on the Cantor ternary set. We consider the asymptotics for the expected total edge length of the directed and undirected nearest-neighbor graph on We prove convergence to a constant of the rescaled expected total edge length of this random graph. The rescaling factor is a function of the fractal dimension and has a log-periodic, nonconstant behavior.

Keywords

Nearest neighborCantor setlaw of large numbers

MSC classification

Primary: 60F05: Central limit and other weak theorems
Secondary: 60D05: Geometric probability and stochastic geometry
Type
Stochastic Geometry and Statistical Applications
Information
Advances in Applied Probability , Volume 41 , Issue 1 , March 2009 , pp. 38 - 62
Copyright
Copyright © Applied Probability Trust 2009 

References

Barbour, A., Holst, L. and Janson, S. (1992). Poisson Approximation (Oxford Stud. Prob. 2). Oxford University Press.Google Scholar
Baryshnikov, Y. and Yukich, J. E. (2005). Gaussian limits for random measures in geometric probability. Ann. Appl. Prob. 15, 213–253.CrossRefGoogle Scholar
Bromwich, T. J. (1942). An Introduction to the Theory of Infinite Series. Macmillan and Company.Google Scholar
Dobos, J. (1996). The standard Cantor function is subadditive. Proc. Amer. Math. Soc. 124, 3425–3426.Google Scholar
Durrett, R. (1996). Probability; Theory and Examples, 2nd edn. Duxbury Press, Belmont, CA.Google Scholar
Gao, J. and Steele, J. M. (1994). General spacefilling curve heuristics and limit theory for the traveling salesman problem. J. Complexity 10, 230–245.CrossRefGoogle Scholar
Grabner, P. J. and Woess, W. (1997). Functional iterations and periodic oscillations for simple random walk on the Sierpiński graph. Stoch. Process. Appl. 69, 127–138.CrossRefGoogle Scholar
Knopfmacher, A. and Prodinger, H. (1996). Explicit and asymptotic formulae for the expected values of the order statistics of the Cantor distribution. Statist. Prob. Lett. 27, 189–194.Google Scholar
Lalley, S. (1990). Traveling salesman with a self-similar itinerary. Prob. Eng. Inf. Sci. 4, 1–18.CrossRefGoogle Scholar
Penrose, M. (2000). Central limit theorems for k-nearest neighbour distances. Stoch. Process. Appl. 85, 295–320.Google Scholar
Penrose, M. D. and Yukich, J. E. (2002). Limit theory for random sequential packing and deposition. Ann. Appl. Prob. 12, 272–301.CrossRefGoogle Scholar
Penrose, M. D. and Yukich, J. E. (2003). Weak laws of large numbers in geometric probability. Ann. Appl. Prob. 13, 277–303.Google Scholar
Platzman, L. K. and Bartholdi, J. J. III. (1989). Spacefilling curves and the planar traveling salesman problem. J. Assoc. Comput. Mach. 36, 719–737.CrossRefGoogle Scholar
Steele, J. M. (1997). Probability Theory and Combinatorial Optimization. Society for Industrial and Applied Mathematics, Philadelphia, PA.Google Scholar
Yukich, J. E. (1998). Probability Theory of Classical Euclidean Optimization Problems (Lecture Notes Math. 1675). Springer, Berlin.Google Scholar