Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T19:49:25.915Z Has data issue: false hasContentIssue false
  • English
  • Français

Obtaining remainder term estimates by an inversion technique

Published online by Cambridge University Press:  01 July 2016

Gunnar Englund
Gunnar Englund*
Affiliation:
Royal Institute of Technology, Stockholm
*
∗Postal address: Department of Mathematics, Royal Institute of Technology, S-100 44 Stockholm, Sweden.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let be a double sequence of random variables such that there exists a ‘dual' sequence satisfying , and that can be expressed as a sum of independent random variables. If 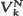(suitably centered and rescaled) is approximately normally distributed as k and N → ∞ in some fashion, we can use this fact to obtain a remainder-term estimate for the asymptotic normality of 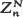as n and N → ∞ in some prescribed manner. The result in the general theorem is used in two specific situations: (i) classical occupancy where the balls can fall through the boxes, (ii) a capture-recapture problem where tagging affects catchability.

Keywords

CENTRAL LIMIT THEOREMCLASSICAL OCCUPANCYCAPTURE–RECAPTURE PROBLEMS
Type
Research Article
Information
Advances in Applied Probability , Volume 16 , Issue 1 , March 1984 , pp. 88 - 110
Copyright
Copyright © Applied Probability Trust 1984 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Van Beek, P. (1972) An application of Fourier methods to the problem of sharpening the Berry-Esseen inequality. Z. Wahrscheinlichkeitsth. 23, 187–196.Google Scholar
Englund, G. (1979) Remainder term estimate for the asymptotic normality of the number of renewals. J. Appl. Prob. 17, 1108–1113.CrossRefGoogle Scholar
Englund, G. (1980) A remainder term estimate for the normal approximation in classical occupancy when the balls can fall through the boxes. Tech. Report TRITA-1981-18, Royal Inst. of Technology, Stockholm.Google Scholar
Englund, G. (1981) A remainder term estimate for the normal approximation in classical occupancy. Ann. Prob. 9, 684–692.CrossRefGoogle Scholar
Farm, A. (1971) Asymptotic normality in a capture-recapture problem when catchability is affected by the tagging procedure. Tech. Report TRITA-MAT-1971-10, Royal Inst. of Technology, Stockholm.Google Scholar
Johnson, N. L. and Kotz, S. (1977) Urn Models and their Applications. Wiley, New York.Google Scholar
Park, C. J. (1972) A note on the classical occupancy problem, Ann. Math. Statist. 43, 1698–1701.Google Scholar
Rényi, A. (1962) Three new proofs and a generalization of a theorem by Irving Weiss. Publ. Math. Inst. Hung. Acad. Sci. 7, 203–214.Google Scholar
Samuel-Cahn, E. (1974) Asymptotic distributions for occupancy and waiting time problems with positive probability of falling through the cells. Ann. Prob. 2, 515–521.CrossRefGoogle Scholar
Samuel-Cahn, E. (1975) Asymptotic distribution for the coupon-collector's and sampling-tagging problems when tagging affects catchability. J. Appl. Prob. 12, 625–628.Google Scholar