Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T17:04:47.170Z Has data issue: false hasContentIssue false
  • English
  • Français

On population-size-dependent branching processes

Published online by Cambridge University Press:  01 July 2016

F. C. Klebaner
F. C. Klebaner*
Affiliation:
University of Melbourne
*
∗Postal address: Department of Statistics, Richard Berry Building, University of Melbourne, Parkville, VIC 3052, Australia.
Get access Rights & Permissions [Opens in a new window]

Abstract

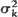We consider a stochastic model for the development in time of a population {Zn} where the law of offspring distribution depends on the population size. We are mainly concerned with the case when the mean mk and the variance of offspring distribution stabilize as the population size k grows to ∞, 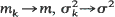The process exhibits different asymptotic behaviour according to m < l, m = 1, m> l; moreover, the rate of convergence of mk to m plays an important role. It is shown that if m < 1 or m = 1 and mn approaches 1 not slower than n–2 then the process dies out with probability 1. If mn approaches 1 from above and the rate of convergence is n–1, then Zn/n converges in distribution to a gamma distribution, moreover 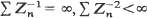a.s. both on a set of non-extinction and there are no constants an, such that Zn/an converges in probability to a non-degenerate limit. If mn approaches m > 1 not slower than n–α, α > 0, and 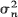do not grow to ∞ faster than nß, β <1 then Zn/mn converges almost surely and in L2 to a non-degenerate limit. A number of general results concerning the behaviour of sums of independent random variables are also given.

Keywords

STOCHASTIC POPULATION MODELHOMOGENEOUS MARKOV CHAINSGREEN FUNCTIONSRECURRENCEEXTINCTIONGROWTH RATESLIMIT THEOREMSSUMS OF INDEPENDENT RANDOM VARIABLES
Type
Research Article
Information
Advances in Applied Probability , Volume 16 , Issue 1 , March 1984 , pp. 30 - 55
Copyright
Copyright © Applied Probability Trust 1984 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Athreya, K. B. and Ney, P. E. (1972) Branching Processes. Springer-Verlag, Berlin.CrossRefGoogle Scholar
[2] Becker, N. (1976) Estimation for an epidemic model. Biometrics 32, 769–777.CrossRefGoogle ScholarPubMed
[3] Chung, K. L. (1960) Markov Chains with Stationary Transition Probabilities. Springer-Verlag, Berlin.CrossRefGoogle Scholar
[4] Feller, W. (1971) An Introduction to Probability Theory and its Applications, Vol. 2. Wiley, New York.Google Scholar
[5] Foster, J. H. (1971) A limit theorem for a branching process with state-dependent immigration. Ann. Math. Statist. 42, 1773–1776.CrossRefGoogle Scholar
[6] Fujimagari, T. (1976) Controlled Galton-Watson process and its asymptotic behaviour. Kodai Math. Sem. Rep. 27, 11–18.CrossRefGoogle Scholar
[7] Harris, J. W. and Kellermeyer, R. W. (1971). The Red Cell: Production, Metabolism, Destruction, Normal and Abnormal. Harvard University Press, Boston MA.Google Scholar
[8] Harris, T. E. (1973) The Theory of Branching Processes. Springer-Verlag, Berlin.Google Scholar
[9] Jagers, P. (1975) Branching Processes with Biological Applications. Wiley, New York.Google Scholar
[10] Kemeny, J. G., Snell, J. L. and Knapp, A. W. (1976) Denumerable Markov Chains. Springer-Verlag, New York.CrossRefGoogle Scholar
[11] Kesten, H. (1971) Some non-linear stochastic growth models. Bull. Amer. Math. Soc. 77, 492–511.CrossRefGoogle Scholar
[12] Kesten, H. (1972) Limit theorems for stochastic growth models I, II. Adv. Appl. Prob. 4, 193–232; 393-428.CrossRefGoogle Scholar
[13] Kesten, H. and Stigum, B. P. (1973) Balanced growth under uncertainty in decomparable economies. In Decision Rules and Uncertainties; NSF-NBER Proceedings. North-Holland, Amsterdam.Google Scholar
[14] Klebaner, F. C. (1983) Population-size-dependent branching process with linear rate of growth. J. Appl. Prob. 20, 242–250.CrossRefGoogle Scholar
[15] Knopp, K. (1928) Theory and Application of Infinite Series. Blackie, London.Google Scholar
[16] Labrovskii, V. A. (1972) A limit theorem for generalized branching process depending on the size of the population. Theory Prob. Appl. 17, 72–85.CrossRefGoogle Scholar
[17] Levina, L. V., Leontovich, A. M. and Pyateskii-Shapiro, I. I. (1968) On regulative branching process. Problemy Peredaci Informacii 4, 72–82.Google Scholar
[18] Loève, M. (1978) Probability Theory I, II. Springer-Verlag, New York.CrossRefGoogle Scholar
[19] Maelzer, D. A. (1970) The regression of log N(n + 1) on log N(n) as a test of density dependence. Ecology 51, 810–822.CrossRefGoogle ScholarPubMed
[20] Pakes, A. G. (1971) A branching process with a state-dependent immigration component. Adv. Appl. Prob. 3, 301–314.CrossRefGoogle Scholar
[21] Rao, K. S. and Kendall, D. G. (1950) On the generalized second limit theorem in the calculus of probabilities. Biometrika 37, 224–230.CrossRefGoogle ScholarPubMed
[22] Schuh, H.-J. (1982) Sums of i.i.d. random variables and an application to the explosion criterion for Markov branching processes. J. Appl. Prob. 19, 29–38.CrossRefGoogle Scholar
[23] Tweedie, R. L. (1975) The robustness of positive recurrence and recurrence of Markov chains under perturbations of the transition probabilities. J. Appl. Prob. 12, 744–752,CrossRefGoogle Scholar
[24] Vasiliev, A. V. (1968) Control of the number of a cell population consisting of cells of two types. Problemy Peredaci Informacii 4, 84–85.Google Scholar