Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zhao-Guo, Chen
1988.
Consistent estimates for hidden frequencies in a linear process.
Advances in Applied Probability,
Vol. 20,
Issue. 02,
p.
295.
Chiu, Shean-Tsong
1989.
Detecting Periodic Components in a White Gaussian Time Series.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 51,
Issue. 2,
p.
249.
Hannan, E. J.
and
Quinn, B. G.
1989.
THE RESOLUTION OF CLOSELY ADJACENT SPECTRAL LINES.
Journal of Time Series Analysis,
Vol. 10,
Issue. 1,
p.
13.
Hannan, E. J.
1993.
Developments in Time Series Analysis.
p.
127.
Wang, Xiaobao
1993.
AN AIC TYPE ESTIMATOR FOR THE NUMBER OF COSINUSOIDS.
Journal of Time Series Analysis,
Vol. 14,
Issue. 4,
p.
433.
Tatum, Lawrence G.
1996.
Control Charts for the Detection of a Periodic Component.
Technometrics,
Vol. 38,
Issue. 2,
p.
152.
Glendinning, R. H.
1997.
Testing for a jump in the periodogram.
Journal of Statistical Computation and Simulation,
Vol. 56,
Issue. 2,
p.
117.
Davis, Richard A.
and
Mikosch, Thomas
1999.
The Maximum of the Periodogram of a Non-Gaussian Sequence.
The Annals of Probability,
Vol. 27,
Issue. 1,
Kokoszka, Piotr
and
Mikosch, Thomas
2000.
The periodogram at the Fourier frequencies.
Stochastic Processes and their Applications,
Vol. 86,
Issue. 1,
p.
49.
Mikosch, Thomas
Resnick, Sidney
and
Samorodnitsky, Gennady
2000.
The maximum of the periodogram for a heavy-tailed sequence.
The Annals of Probability,
Vol. 28,
Issue. 2,
Glendinning, Richard H.
2003.
On The Properties Of Random Entire Functions.
Stochastic Analysis and Applications,
Vol. 21,
Issue. 2,
p.
359.
Islam, M. Shahidul
2011.
Testing Periodicity in Short Series and Application to Gene Expression Data.
Communications in Statistics - Simulation and Computation,
Vol. 40,
Issue. 4,
p.
561.
Nadler, B
and
Kontorovich, A
2011.
Model Selection for Sinusoids in Noise: Statistical Analysis and a New Penalty Term.
IEEE Transactions on Signal Processing,
Vol. 59,
Issue. 4,
p.
1333.
Davis, Richard A.
Lii, Keh-Shin
and
Politis, Dimitris N.
2011.
Selected Works of Murray Rosenblatt.
p.
388.
Turkman, K.F.
2012.
Time Series Analysis: Methods and Applications.
Vol. 30,
Issue. ,
p.
565.
Xiao, Han
and
Wu, Wei Biao
2012.
Covariance matrix estimation for stationary time series.
The Annals of Statistics,
Vol. 40,
Issue. 1,
Talebi, Farzad
and
Pratt, Thomas
2015.
Model Order Selection for Complex Sinusoids in the Presence of Unknown Correlated Gaussian Noise.
IEEE Transactions on Signal Processing,
Vol. 63,
Issue. 7,
p.
1664.
Shutin, Dmitriy
and
Vexler, Boris
2017.
Sparse Bayesian learning with dictionary refinement for super-resolution through time.
p.
1.
Sulis, Sophia
Mary, David
and
Bigot, Lionel
2017.
A Study of Periodograms Standardized Using Training Datasets and Application to Exoplanet Detection.
IEEE Transactions on Signal Processing,
Vol. 65,
Issue. 8,
p.
2136.
Leitinger, Erik
Grebien, Stefan
Fleury, Bernard
and
Witrisal, Klaus
2020.
Detection and Estimation of a Spectral Line in MIMO Systems.
p.
1090.

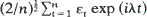 exp
exp 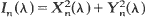 . It is shown that as
. It is shown that as 